Giáo trình: Lý thuyết cán - Chương 7: Cán nghiêng

Chia sẻ: Nguyễn Văn Đức Duc | Ngày: | Loại File: PDF | Số trang:12

Thêm vào BST

Báo xấu

124
lượt xem 19
download

Giáo trình: Lý thuyết cán - Chương 7: Cán nghiêng

Mô tả tài liệu

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Cán nghiêng có thể thực hiện theo sơ đồ khác nhau tùy thuộc vào hình dáng của trục cán.

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Giáo trình: Lý thuyết cán - Chương 7: Cán nghiêng

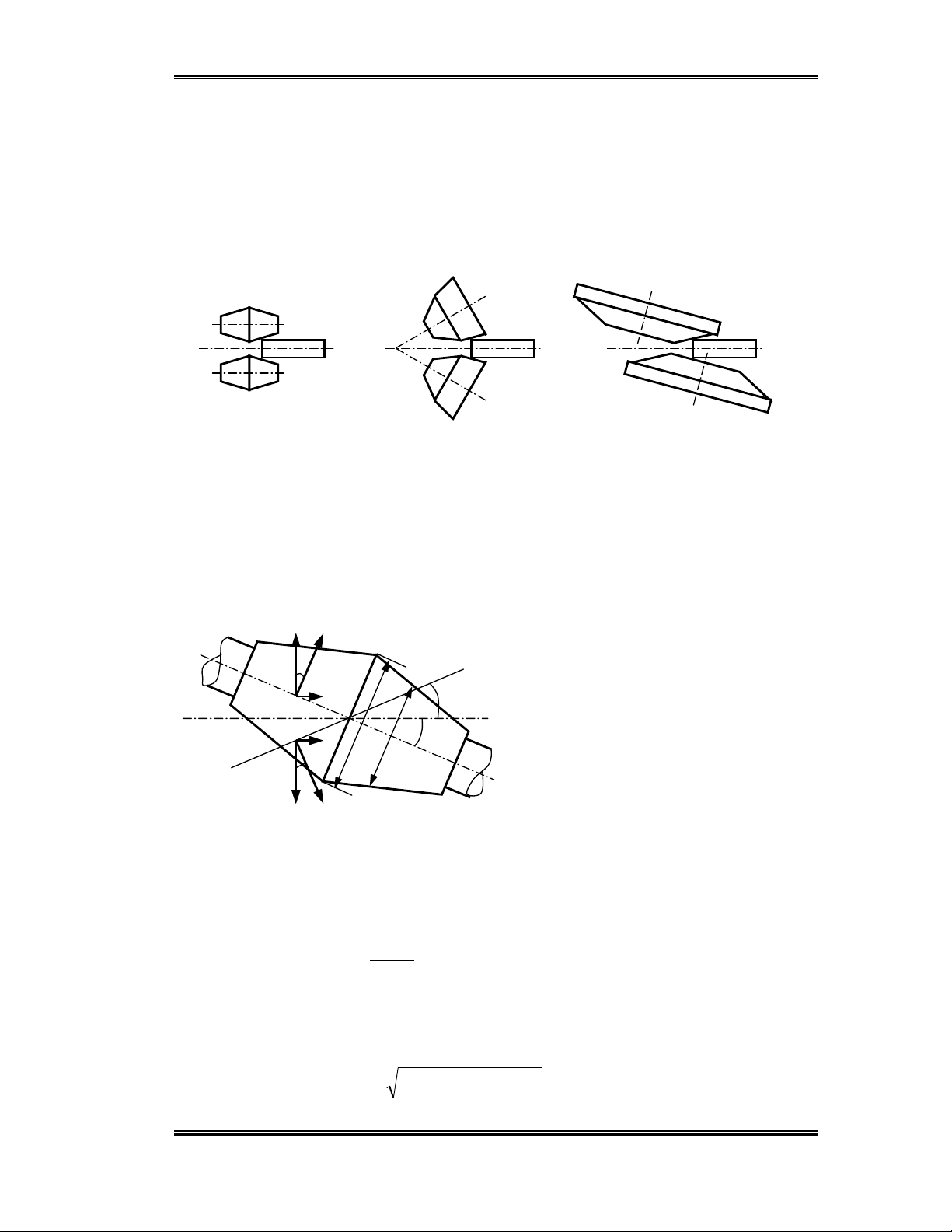
Gi¸o tr×nh: Lý thuyÕt c¸n Ch−¬ng 7 C¸n nghiªng 7.1- C¸c kh¸i niÖm vÒ c¸n nghiªng C¸n nghiªng cã thÓ thùc hiÖn theo s¬ ®å kh¸c nhau tïy thuéc vµo h×nh d¸ng cña trôc c¸n (h×nh 7.1). a) b) c) H×nh 7.1- S¬ ®å nguyªn lý c¸n ngang - nghiªng a) Trôc tang trèng c«n; b) Trôc h×nh nÊm c«n; c) Trôc h×nh ®Üa Dï c¸n ë d¹ng trôc nµo th× vÒ nguyªn lý c¸n ngang - nghiªng còng kh«ng thay ®æi. Chóng ta h·y kh¶o s¸t tr−êng hîp c¸n trªn trôc tang trèng c«n. Víi ph«i lu«n cã hai chuyÓn ®éng: chuyÓn ®éng quay vµ chuyÓn ®éng tÞnh tiÕn. Lo¹i trôc tang trèng cßn ®−îc øng dông rÊt phæ biÕn khi c¸n t¹o ph«i rçng cho c«ng nghÖ c¸n èng kh«ng hµn (h×nh 7.2). CT C Tõ h×nh ta cã: A β B C0 = C.sinβ CT = C.cosβ (7.1) C0 β O O V× cã sù tr−ît gi÷a trôc c¸n DH β vµ ph«i nªn: B C0 D C0 = i0.C.sinβ β A CT = iT.C.cosβ (7.2) CT C víi, i0 vµ iT lµ hai hÖ sè tr−ît H×nh 7.2- Nguyªn lý c¸n ngang - nghiªng chiÒu trôc vµ h−íng tang. t¹o ph«i èng ®Ó c¸n èng kh«ng hµn TrÞ sè gãc β th−êng dao ®éng trong kho¶ng 6 ÷ 8 , ®«i khi ®¹t 15 . 0 0 0 Tèc ®é quay cña trôc c¸n: π.D.n C= (m / s) 60 Gäi CM lµ tèc ®é cña kim lo¹i nhËn ®−îc tõ trôc c¸n, ta cã: CM = C.i (7.3) víi, i lµ hÖ sè c«ng suÊt truyÒn t¶i. HoÆc: CM = (C o i 0 )2 + (C T i T )2 (7.4) Tõ c¸c biÓu thøc (7.2), (7.3) vµ (7.4) ta suy ra: Tr−êng §¹i häc B¸ch khoa - §¹i häc §µ N½ng 88
Gi¸o tr×nh: Lý thuyÕt c¸n i= (i 0 sin β)2 + (i T cos β)2 (7.5) Trong c¸n ngang, ta cã gãc β = 0 nªn: i = iT Trong c¸n däc, ta cã gãc β = π/2 nªn: i = i0 Khi c¸n ngang - nghiªng, theo sè liÖu thùc nghiÖm cña Metveep I.M trªn m¸y khoan t¹o ph«i èng tõ thái ®óc th×: i 0 = 0,75 + 0,01d H − 0,008β d c − 800 (7.6) Khi t¹o ph«i rçng tõ ph«i ®Æc: + 0,005d H + (0,025 + 0,000135d z )β 3,2 i0 = (7.7) C trong ®ã, dc: ®−êng kÝnh thái ®óc, mm dH: ®−êng kÝnh cña ph«i vµ thái ®óc t¹i vïng biÕn d¹ng, mm dz: ®−êng kÝnh cña ph«i, mm C: tèc ®é quay cña trôc c¸n, m/s β: gãc nghiªng (h×nh 7.2) HÖ sè tr−ît chiÒu trôc iT trong kho¶ng 0,85 ÷ 1,05 (sè liÖu thùc nghiÖm). Tõ sù ph©n tÝch trªn ®©y, khi c¸n ngang - nghiªng trÞ sè gãc β thay ®æi tïy theo tû sè cña hÖ sè tr−ît chiÒu trôc vµ hÖ sè tr−ît tiÕp tuyÕn (h×nh 7.3). C0M C0 Ta gi¶ thiÕt r»ng, tèc ®é tÞnh C0M tiÕn vµ tèc ®é quay cña ph«i βM βM h×nh thµnh mét tèc ®é tæng hîp CTM β CM cã ph−¬ng t¹o víi tèc ®é quay CTM CM mét gãc lµ βM (h×nh 7.3a). Trªn a) thùc tÕ, tån t¹i sù tr−ît gi÷a trôc CT C b) vµ ph«i nªn quan hÖ tèc ®é nµy H×nh 7.3- Quan hÖ tèc ®é chiÒu trôc cã sù thay ®æi vµ thÓ hiÖn qua vµ tiÕp tuyÕn gãc β (h×nh 7.3b). Cã nghÜa lµ a) Cña kim lo¹i ph−¬ng cña tèc ®é cña kim lo¹i b) Cña kim lo¹i vµ trôc c¸n khi β>βM phô thuéc vµo tû sè cña hai hÖ sè tr−ît nh− trªn (h×nh 7.3), ta cã: C i tgβ M = 0M = 0 tgβ (7.8) C TM i T Th«ng th−êng, ta cã i0 < iT do ®ã, βM < β nÕu nh− hÖ sè tr−ît i > 1 th× tèc ®é tuyÖt ®èi cña kim lo¹i lín h¬n tèc ®é quay cña trôc. C¸c nghiªn cøu thùc nghiÖm cho thÊy, hÖ sè tr−ît theo chiÒu trôc trªn m¸y c¸n nghiªng 3 trôc nhá h¬n so víi m¸y 2 trôc kho¶ng 20 ÷ 60% vµ tiªu hao n¨ng Tr−êng §¹i häc B¸ch khoa - §¹i häc §µ N½ng 89
Gi¸o tr×nh: Lý thuyÕt c¸n l−îng kho¶ng 1,5 ÷ 1,8 lÇn, bëi v× ë m¸y 3 trôc ®iÒu kiÖn ¨n ph«i tèt h¬n vµ kh«ng cÇn sö dông th−íc ®Þnh h−íng. Víi mét l−îng Ðp ®ñ lín ë ®Çu mòi khoan th× hÖ sè tr−ît chiÒu trôc ë m¸y 3 trôc lµ i0 = 1,01 ÷ 1,07 vµ ë m¸y 2 trôc lµ i0 = 0,9. Nh− vËy, ë m¸y 3 trôc cã hiÖn t−îng v−ît tr−íc: F C 0M = C H . H (7.9) F víi, C0M, F: tèc ®é, diÖn tÝch tiÕt diÖn t¹i mét mÆt c¾t bÊt kú trong vïng biÕn d¹ng CH, FH: tèc ®é, diÖn tÝch tiÕt diÖn t¹i mÆt c¾t cã ®−êng kÝnh trôc c¸n lín nhÊt. π.D M .n C H = i0 sin β (7.10) 60 ⎛ π.D H .n ⎞F C 0M = ⎜ i 0 sin β ⎟ H (7.11) ⎝ 60 ⎠ F Gäi S lµ b−íc dÞch chuyÓn cña ph«i, ta cã: S = C0M.τ (7.12) trong ®ã, τ: thêi gian ®Ó quay ®−îc ph«i 1/2 vßng. 60 τ= (7.13) 2 .n z víi nz lµ sè vßng quay cña ph«i trong mét phót C Suy ra, S = 0M .30 (7.14) nz Sè vßng quay cña ph«i trong mét phót (nz) cã thÓ tÝnh tõ ®iÒu kiÖn c©n b»ng: π.D.n π.d.n z iT . cos β = (7.15) 60 60 D Suy ra, n z = i T .n. . cos β (7.16) d KÕt hîp gi÷a c¸c biÓu thøc (7.11), (7.14) vµ (7.16) ta cã: i D F d S = 3,14. 0 . H . H . 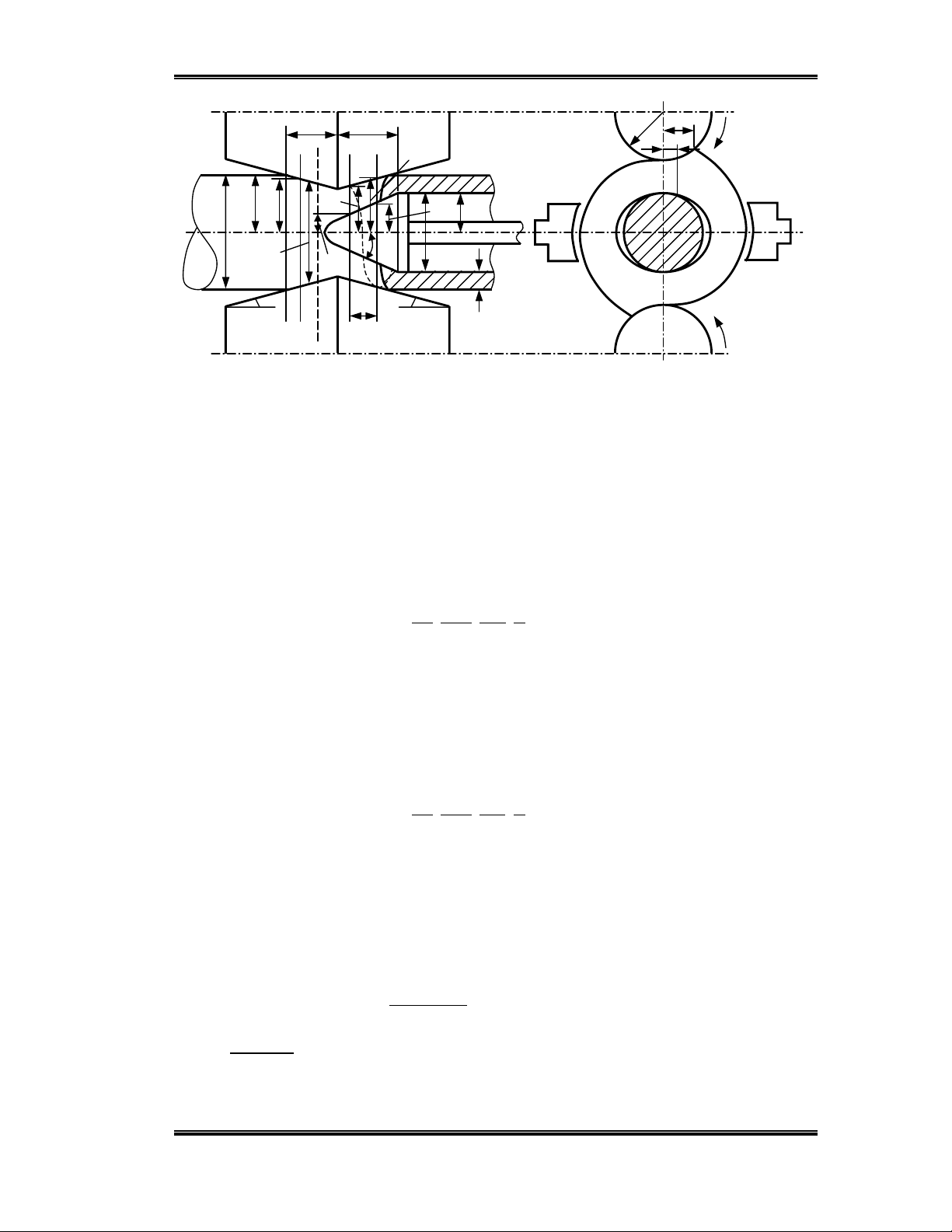tgβ (7.17) iT D F 2 C¸c th«ng sè cña vïng biÕn d¹ng khi t¹o ph«i èng nh− h×nh 7.4. 7.2- DiÖn tÝch bÒ mÆt tiÕp xóc khi khoan èng Nh− h×nh 7.4 ta thÊy sau 1/2 vßng quay cña ph«i th× nã ®−îc tÞnh tiÕn mét ®o¹n lµ s. Trong qu¸ tr×nh Êy th× ®−êng kÝnh (chiÒu dµy thµnh èng) gi¶m mét l−îng lµ ∆r (trôc c¸n trªn lâi tùa). ChiÒu réng cña bÒ mÆt tiÕp xóc lµ b, tÝnh theo biÓu thøc (6.6) b = ∆r.d trong ®ã, ∆r = (r1’ - r1’’) - (r2’ - r2’’) = (r2’’ - r1’’) - (r2’ - r1’) Tr−êng §¹i häc B¸ch khoa - §¹i häc §µ N½ng 90
Gi¸o tr×nh: Lý thuyÕt c¸n I II D S bm 1 2 n 1 2 r2’ r1 r2 r1’ r2’’ rm d3 dm d γ r1’’ S tr α1 α2 12 n 1 2 H×nh 7.4- Vïng biÕn d¹ng khi c¸n ngang - nghiªng trªn m¸y 2 trôc (trôc tang trèng c«n) Nh− trªn h×nh 7.4, ta cã: r2’ - r1’ = Stgα2 r2’’ - r1’’ = Stgγ VËy, ∆r = S(tgγ - tgα2) (7.18) víi, α2: gãc nghiªng cña trôc c¸n ë vïng II cña vïng biÕn d¹ng. γ: gãc nghiªng cña mòi khoan (lâi tùa). Thay S ë biÓu thøc (7.17) vµo ta cã: i D F d ∆r = 3,14. 0 . H . H . tgβ.( tgγ − tgα 2 ) (7.19) iT D F 2 ChiÒu réng cña mét bÒ mÆt tiÕp xóc t¹i mét tiÕt diÖn nµo ®ã cña vïng I (h×nh 7.4) cña vïng biÕn d¹ng còng trªn c¬ së cña l−îng Ðp ∆r. Gi¶ thiÕt r»ng, tr−íc mòi khoan ch−a h×nh thµnh lç rçng tõ h×nh 7.4 ta cã: ∆r = r1 - r2 = S.tgα1 (7.20) víi, α1: gãc nghiªng cña trôc c¸n tõ phÝa ph«i ®i vµo. i D F d Nh− vËy, ∆r = 3,14. 0 . H . H . tgβ.( tgα1 ) (7.21) iT D F 2 Trªn c¬ së l−îng biÕn d¹ng ∆r chóng ta cã thÓ tÝnh ®−îc chiÒu réng cña bÒ mÆt tiÕp xóc b theo biÓu thøc (6.6). V× khi c¸n ngang - nghiªng, chiÒu réng b thay ®æi theo chiÒu dµi cña vïng biÕn d¹ng nªn diÖn tÝch tiÕp xóc ph¶i lµ tæng cña tõng vïng theo tõng chiÒu dµi ∆l vµ chiÒu réng b. b + b n +1 F=∑ n .∆l (7.22) 2 VÝ dô 1: X¸c ®Þnh kÝch th−íc cña bÒ mÆt tiÕp xóc khi khoan vá èng trªn m¸y 2 trôc kiÓu tang trèng c«n. §−êng kÝnh trôc t¹i vïng biÕn d¹ng bÐ nhÊt DH = 700mm, víi α1 = α2 = 33,50; gãc β = 60; i0 = 0,9; iT = 1; ϕ = 2; d3 = 105mm; ®−êng Tr−êng §¹i häc B¸ch khoa - §¹i häc §µ N½ng 91
Gi¸o tr×nh: Lý thuyÕt c¸n kÝnh ngoµi cña vá èng df = 105mm; chiÒu dµy thµnh èng t = 10mm; ®−êng kÝnh mòi khoan dm = 85mm; chiÒu dµi mòi khoan lTB = 154mm; kho¶ng c¸ch gi÷a hai trôc t¹i tiÕt diÖn nhá nhÊt cña vïng biÕn d¹ng lµ l = 90mm. TÝnh diÖn tÝch tiÕp xóc? - ChiÒu dµi cña vïng I: 105 − 90 lI = = 123 mm 2.3,50 - ChiÒu dµi cña vïng II: 107 − 90 l II = = 139 mm 2.3,50 - Tg cña gãc c«n mòi khoan: 85 − 10 tgγ = = 0,24 2.154 §−êng kÝnh èng t¹i ®−êng kÝnh lín nhÊt cña mòi khoan lµ: 85 + 2.10 = 105mm víi gãc β = 3,50; t−¬ng øng víi mét kho¶ng c¸ch kÓ tõ tiÕt diÖn nhá nhÊt cña vïng biÕn d¹ng l = 123mm cho nªn mòi khoan v−ît qu¸ tiÕt diÖn nhá nhÊt cña vïng biÕn d¹ng mét ®é dµi lµ: 154 - 123 = 31mm. Ta chia vïng I vµ II b»ng c¸c tiÕt diÖn th¼ng ®øng thµnh c¸c ®é dµi ∆l (b¶ng 7.1). Ta tÝnh l−îng Ðp sau 1/2 vßng quay ®èi víi vïng I theo biÓu thøc (7.21) vµ víi vïng II theo biÓu thøc (7.19). KÕt qu¶ tÝnh to¸n nh− ë b¶ng 7.1. Sè liÖu tÝnh to¸n cña vÝ dô trªn B¶ng 7.1 Vïng S/l−îng ∆l d D F ∆r B *Fk bCD d0t tiÕt diÖn (mm) (mm) (mm) (mm2) (mm) (mm) (mm2) (mm) (mm) 0 - 105 685 8600 0 0 - - - 1 30 102 688 8150 0,067 5,2 78 - I 2 31 98 692 7500 0,069 5,2 161 57 - 3 31 94 696 6800 0,220 9,0 220 10 4 31 90 700 5900 0,226 9,0 279 25 5 31 94 696 5650 0,240 9,5 286 40 6 31 98 692 5150 0,285 10,6 310 55 II 7 31 102 688 4320 0,350 11,9 347 9,4 60 8 30 105 685 3000 0,530 14,9 402 85 9 16 107 683 3000 0 0 120 - b + b n +1 * Fk = n ∆l n +1 2 7.3- ¸p lùc kim lo¹i lªn trôc c¸n cña m¸y khoan Theo c¸c sè liÖu thùc nghiÖm cho thÊy r»ng, víi c¸n ngang - nghiªng th× sù ph©n bè lùc ®¬n vÞ vµ lùc ma s¸t cã d¹ng parabol låi, ®Ønh cùc ®¹i ë gÇn tiÕt diÖn mµ t¹i ®ã ph«i ®i vµo trôc c¸n, cã nghÜa lµ trªn bÒ mÆt tiÕp xóc chØ cã mét vïng trÔ. Tr−êng §¹i häc B¸ch khoa - §¹i häc §µ N½ng 92
Gi¸o tr×nh: Lý thuyÕt c¸n Còng tõ c¸c kÕt qu¶ thùc nghiÖm cho thÊy, nÕu cµng t¨ng l−îng Ðp tû ®èi b/D vµ d/D th× øng suÊt ph¸p tiÕp xóc sÏ gi¶m ®i. Theo Tremarep T. P th× trÞ sè øng suÊt tiÕp trªn bÒ mÆt tiÕp xóc cã gi¸ trÞ cùc ®¹i ë vïng I vµ gi¶m dÇn theo ®é c«n c¸n. Nh− vËy th× trÞ sè øng suÊt ph¸p trªn bÒ mÆt tiÕp xóc chÞu ¶nh h−ëng chñ yÕu cña vïng cung bªn ngoµi vïng biÕn d¹ng. Cµng t¨ng kh¶ n¨ng tr−ît chiÒu trôc th× ¸p lùc trªn trôc c¸n cµng gi¶m ®i do sù gi¶m l−îng Ðp ®¬n vÞ. Qua h×nh 7.5 ta cã nhËn xÐt: P, MH vïng I cã l−îng Ðp ph«i theo 2 (kG/mm ) h−íng kÝnh, vïng II lµ qu¸ tr×nh c¸n máng ph«i trªn mòi khoan 270(30) ®Ó t¹o thµnh vá æng. 196(20) T¹i vïng I cã tû sè gi÷a 98(10) chiÒu réng vµ ®−êng kÝnh cña 0 ph«i rÊt nhá (0,05 ÷ 0,2). T¹i 10 20 b, mm vïng II tû sè gi÷a chiÒu réng vµ chiÒu dµy vá èng vµi phÇn 10 ®¬n H×nh 7.5- §å thÞ øng suÊt ph¸p vÞ ë ®Çu mòi khoan vµ kh«ng v−ît tiÕp xóc trªn m¸y khoan vá èng qu¸ 1 ë vïng t¹o h×nh, nãi kh¸c ®i lµ vÒ quan hÖ kÝch th−íc h×nh häc rÊt nhá cho nªn lùc ma s¸t trªn bÒ mÆt tiÕp xóc kh«ng lín. V× vËy, hÖ sè nσ trong biÓu thøc (4.36) cã thÓ coi b»ng 1 (nσ = 1). BiÓu thøc (4.36) khi khoan èng lµ: p = nβ.nH.nz.nv.σS Ph©n tÝch biÓu thøc nµy ta thÊy: - Khi khoan èng th× ®¹i l−îng d·n dµi cña ph«i sau 1/2 vßng quay lµ kh«ng lín nªn qu¸ tr×nh biÕn d¹ng cã thÓ coi lµ biÕn d¹ng ph¼ng nªn: nβ = 1,155 - Qu¸ tr×nh khoan thùc hiÖn ë nhiÖt ®é cao: nH = 1 C¸c hÖ sè nβ vµ nH ë vïng I vµ II lµ nh− nhau. - HÖ sè nz (¶nh h−ëng cña vïng cøng bªn ngoµi vïng biÕn d¹ng) vµ hÖ sè nv (¶nh h−ëng cña tèc ®é biÕn d¹ng) ë trªn mçi tiÕt diÖn cã sù kh¸c nhau. Tuy nhiªn ta vÉn cã thÓ lÊy mét gi¸ trÞ trung b×nh cho c¶ hai vïng I vµ II: b TB n zI = 2 − (7.23) d TB 1 n trong ®ã, b TB = ∑ b víi b = ϕ ∆r.d n 0 (7.24) dz + dH d TB = (7.25) 2 Tr−êng §¹i häc B¸ch khoa - §¹i häc §µ N½ng 93
Gi¸o tr×nh: Lý thuyÕt c¸n víi, dz, dH: ®−êng kÝnh cña ph«i lóc vµo trôc c¸n vµ t¹i tiÕt diÖn nhá nhÊt cña vïng biÕn d¹ng. b TB n zII = 2 − (7.26) t TB trong ®ã, tTB: chiÒu dµy trung b×nh cña vá èng t +t t TB = H r (7.27) 2 víi, tH: chiÒu dµy ph«i tr−íc mòi khoan tr: chiÒu dµy vá èng - §Ó x¸c ®Þnh ®−îc hÖ sè nv cÇn ph¶i biÕt tèc ®é biÕn d¹ng tû ®èi. Ký hiÖu tèc ®é biÕn d¹ng tû ®èi lµ Ux ta cã vïng I: 2C z Ux = (ë mäi tiÕt diÖn) d víi, Cz: thµnh phÇn tèc ®é th¼ng ®øng cña tèc ®é ®−a ph«i. Cz = Cx.tgα 2C x VËy, Ux = tgα (7.28) d Tèc ®é biÕn d¹ng trung b×nh trong vïng I lµ: π.n F C x = i0 D H . sin β. H 60 F Ta ký hiÖu tèc ®é ®−a ph«i lóc vµo vïng I lµ Cxz vµ lóc ra khái vïng I lµ CxH: 2 π.n ⎛d ⎞ C xz = i0 D H . sin β.⎜ H ⎜d ⎟ ⎟ 60 ⎝ z ⎠ π.n C xH = i 0 D H . sin β 60 Tèc ®é trung b×nh cña ph«i lµ: 2 1 π.n ⎛ d ⎞ C TB = i0 D H . sin β.⎜1 + H ⎜ ⎟ ⎟ (7.29) 2 60 ⎝ dz ⎠ §−êng kÝnh trung b×nh cña ph«i ë vïng I: d + dH d TB = z (7.30) 2 Thay hai biÓu thøc (7.29) vµ (7.30) vµo (7.28), ta cã: 2 ⎛d ⎞ 1+ ⎜ H ⎟ ⎜d ⎟ π.n D H U I = 2i 0 . . sin β.tgα1 . ⎝ z ⎠ (7.31) 60 d z d 1+ H d §èi víi vïng II ta cã: Tr−êng §¹i häc B¸ch khoa - §¹i häc §µ N½ng 94
Gi¸o tr×nh: Lý thuyÕt c¸n 2C x Ux = tgα 2 (7.32) tx trong ®ã, tx: chiÒu dµy vá èng khi khoan Tèc ®é ®−a ph«i vµo vïng II vµ ra khái vïng II lµ: π.n C xH = i 0 D H . sin β 60 π.n F C x0 = i 0 D H . sin β. H 60 F0 TrÞ sè trung b×nh lµ: 1 π.n ⎛ F ⎞ C TB = i 0 D H . sin β.⎜1 + H ⎜ ⎟ ⎟ (7.33) 2 60 ⎝ F0 ⎠ ChiÒu dµy vá èng trong vïng II: t +t t TB = H 0 (7.34) 2 trong ®ã, tH vµ t0 lµ diÖn tÝch tiÕt diÖn cña èng khi khoan. Thay hai biÓu thøc (7.33) vµ (7.34) vµo (7.32) ta cã: F 1+ H π.n D H F0 U II = 2i 0 . . sin β.tgα 2 . (7.35) 60 t 0 tH 1+ t0 Khi cã ®−îc tèc ®é biÕn d¹ng chóng ta c¨n cø vµo ®ã ®Ó t×m ®−îc ¶nh h−ëng cña tèc ®é ®Õn giíi h¹n bÒn vµ tÝnh dÎo cña vËt liÖu, cã nghÜa lµ ta cã thÓ x¸c ®Þnh ®−îc hÖ sè nv (th−êng ®−îc t×m theo ®å thÞ). Khi biÕt trë kh¸ng biÕn d¹ng thùc cña vïng I vµ II ta cã thÓ t×m ®−îc ¸p lùc cña kim lo¹i lªn trôc c¸n: p = KI.FI + KII.FII (7.36) trong ®ã, FI vµ FII lµ diÖn tÝch bÒ mÆt tiÕp xóc cña vïng I vµ II. VÝ dô 2: X¸c ®Þnh ¸p lùc lªn trôc c¸n cña m¸y khoan èng cã c¸c sè liÖu nh− ë vÝ dô 1; nhiÖt ®é kim lo¹i khi khoan lµ 11500C; σS = 32 MN/m2 (3,2 kG/mm2); sè vßng quay cña trôc c¸n n = 120 v/p. - TÝnh ®−êng kÝnh trung b×nh cña ph«i: d + d H 105 + 90 d TB = z = = 97,5 (mm) 2 2 - TÝnh chiÒu dµy trung b×nh cña vá èng: t +t 35,5 + 10 t TB = H 0 = = 21,5 (mm) 2 2 - X¸c ®Þnh hÖ sè nz: Tr−êng §¹i häc B¸ch khoa - §¹i häc §µ N½ng 95
Gi¸o tr×nh: Lý thuyÕt c¸n b TB 5,7 n zI = 2 − =2− = 1,76 d TB 97,5 b TB 9,4 n zII = 2 − =2− = 1,34 t TB 21,5 - TÝnh tèc ®é biÕn d¹ng trung b×nh: + Vïng I: 2 ⎛ 90 ⎞ 1+ ⎜ ⎟ π.120 700 ⎝ 105 ⎠ = 4,7 (1 / s ) U I = 2.0,9. . 0 0 . sin 6 .tg3 30'. 60 105 90 1+ 105 + Vïng II: 5900 1+ π.120 700 U II = 2.0,9 . . sin 6 0.tg30 30'. 3000 = 11,4 (1 / s ) 60 105 32,5 1+ 10 - C¨n cø vµo tèc ®é biÕn d¹ng ë vïng I vµ II theo ®å thÞ ta x¸c ®Þnh ®−îc hÖ sè nv khi cã U vµ nhiÖt ®é c¸n: nvI = 2,2; nvII = 3,2 (xem h×nh 5.15). Nh− vËy, trë kh¸ng biÕn d¹ng KI vµ KII nh− sau: KI = 1,155.1.1,76.2,2.32 = 141 MN/m2 (14,1 kG/mm2) KII = 1,155.1.1,34.3,2.32 = 142 MN/m2 (14,2 kG/mm2) ¸p lùc toµn phÇn lªn trôc c¸n: P = KI.FI + KII.FII = 141.740 + 142.1470 = 313000 MN (≈ 31,3 tÊn) 7.4- Lùc chiÒu trôc lªn mòi khoan cña m¸y khoan èng §Ó gi¶i bµi to¸n b»ng ¸p lùc lªn mòi khoan ta ®· gi¶ thiÕt r»ng ¸p lùc trung b×nh ë ®Çu mòi khoan, tæng ¸p lùc lªn mòi khoan, c«ng tiªu thô trong khi khoan lµ nhá nhÊt nÕu nh− ®¹t ®−îc mét l−îng Ðp hîp lý tr−íc mòi khoan. ChØ nh− vËy th× l−îng Ðp tû ®èi lµ kh«ng lín so víi ®−êng kÝnh trôc c¸n ë vïng tr−íc vïng biÕn d¹ng, øng suÊt ®−îc coi lµ øng suÊt ph¼ng. TrÞ sè øng suÊt σz ®−îc tÝnh theo c«ng thøc: θ σz ⎛ρ⎞ r 1 = −2⎜ ⎟ e fθ + ln − (7.37) K ⎝r⎠ ρ 2 Ký hiÖu ¸p lùc chiÒu trôc lªn mòi khoan lµ Q, ta cã: γ rm a γ rm ⎛ ρ ⎞ fθ ⎛ r 1⎞ Q = ∫ σ z dF = −2 K ∫ ∫ ⎜ ⎟ e .ρ.dρ.dθ + K ∫ ∫ ⎜ ln ρ − 2 ⎟ρ.dρ (7.38) ⎜ ⎟ F 0 0 ⎝r⎠ 0 0 ⎝ ⎠ víi, rm: b¸n kÝnh mòi khoan t¹i tiÕt diÖn lín nhÊt. LÊy tÝch ph©n biÓu thøc (7.38) theo gãc θ, ta cã: Tr−êng §¹i häc B¸ch khoa - §¹i häc §µ N½ng 96
Gi¸o tr×nh: Lý thuyÕt c¸n e fθ − 1 rm a rm ⎛ρ⎞ ⎛ r 1⎞ Q = −2 K f ∫ ⎜ ⎟ ρ.dρ + Kγ ⎝r⎠ ∫ ⎜ ln ρ − 2 ⎟ρ.dρ ⎜ ⎝ ⎟ ⎠ (7.39) 0 0 ë ®©y ta cã: rm ρa + 2 rm a a ⎛ρ⎞ r2 ⎛ r ⎞ ∫ ⎜ ⎟ ρ.dρ = a ⎝r⎠ r (a + 2 ) 0 = m ⎜ m⎟ a+2⎝ r ⎠ (7.40) 0 rm r r ⎛ r 1⎞ m ρ 1 m ∫ ⎜ ln − ⎟ρ.dρ = − ∫ ρ. ln .dρ − ∫ ρ.dρ ⎜ ρ 2⎟ ⎝ ⎠ r 2 0 (7.41) 0 0 ρ BiÕn ®æi biÓu thøc (7.41), ký hiÖu = ξ → ρ = ξ.r ; dρ = r.dξ r rm ⎛ rm ⎞ rm ρ r ⎜ 2⎛ 1 1⎞ r ⎟ − ∫ ρ ln .dρ = − r 2 ∫ ξ. ln ξ.dξ = − r 2 ⎜ ξ ⎜ ln ξ − ⎟ r ⎜ ⎝2 4⎠0 ⎟ ⎟ 0 0 ⎝ ⎠ 2 2 2 ⎛ rm ⎞ ⎛ 1 rm 1 ⎞ rm rm rm = − r .⎜ ⎟ ⎜ ln 2 − ⎟ = − ln + ⎝ r ⎠ ⎝2 r 4⎠ r r 4 rm 2 1 rm 2 ∫ ρ.dρ = 4 0 rm ⎛ r 1⎞ r2 r Suy ra, ∫ ⎜ ln − ⎟ρ.dρ = m ln ⎜ ρ 2⎟ ⎝ ⎠ 2 rm (7.42) 0 Nh− vËy, lùc Q cã gi¸ trÞ: e fθ − 1 rm ⎛ rm ⎞ 2 a r2 r Q = −2 K ⎜ ⎟ + Kγ m ln (7.43) f a+2⎝ r ⎠ 2 rm e fγ − 1 1 + fγ − 1 MÆt kh¸c, ≈ = γ v× trªn thùc tÕ gãc γ rÊt bÐ vµ f
Gi¸o tr×nh: Lý thuyÕt c¸n r rm + t 0 ⎛ ⎞ t0 t ln = ln = ln⎜1 + 0 ⎟≈ ⎜ r ⎟ r rm rm ⎝ ⎠ m m KÕt hîp tÊt c¶ c¸c gi¸ trÞ võa t×m ®−îc víi c¸c gi¶ thiÕt nhÊt ®Þnh, ta cã gi¸ trÞ cña lùc chiÒu trôc Q nh− sau: 2 ⎛ t ⎞ Q = K.γ.rm .⎜1 − 0 ⎟ ⎜ 2. r ⎟ (7.44) ⎝ m ⎠ b Nh− ë h×nh 7.4, ta cã: γ = m nªn: rm ⎛ t ⎞ Q = K.b m .rm .⎜1 − 0 ⎜ 2.r ⎟ ⎟ (7.45) ⎝ m ⎠ ¸p lùc ®¬n vÞ q t¸c dông lªn mòi khoan lµ: Q 1 ⎛ t ⎞ q= hoÆc q = K ⎜1 − 0 ⎜ d ⎟ ⎟ (7.46) b m .2.rm 2 ⎝ m ⎠ Th−êng tû sè t0/dm kho¶ng 0,1 ÷ 0,4; cho nªn: q = (0,3 ÷ 0,45)K (7.47) C¸c nghiªn cøu thùc nghiÖm cho thÊy: q = (0,6 ÷ 0,8)σS ë chÝnh t©m ®Çu mòi khoan: q = (0,2 ÷ 0,4)σS Sù nghiªn cøu lý thuÕt vµ thùc nghiÖm cho ta kh¼ng ®Þnh r»ng, mòi khoan dÔ dµng nÐn vµo kim lo¹i v× t¹i ®Çu mòi khoan ¸p lùc trung b×nh lu«n < 1/2 trë kh¸ng biÕn d¹ng cña vËt liÖu. Trong tr−êng hîp biÕt tr−íc q th× còng cã thÓ tÝnh Q theo biÓu thøc: Q = q.bm.dm (7.48) Khi c¸n ngang th× tû sè gi÷a lùc chiÒu trôc vµ lùc cña trôc c¸n t¸c dông lªn kim lo¹i cã gi¸ trÞ: Q = 0,2 ÷ 0,5 q 7.5- L−îng Ðp tíi h¹n khi c¸n ngang - nghiªng Khi c¸n ngang - nghiªng, tr¹ng th¸i øng suÊt lµ tr¹ng th¸i øng suÊt ph¼ng, sù ph¸ huû chñ yÕu lµ do tr−ît. L−îng Ðp tíi h¹n khi c¸n kh«ng lâi tùa nhá h¬n so víi khi khoan vá èng (c¸n cã lâi tùa). L−îng Ðp tíi h¹n phô thuéc vµo nhiÖt ®é cña tõng m¸c thÐp, thµnh phÇn ho¸ häc cña ph«i c¸n (theo c¸c sè liÖu nghiªn cøu cho thÊy nÕu tû sè gi÷a Cr vµ Vanadi t¨ng tõ 1,6 lªn 1,8 th× sè l−îng phÕ phÈm do bÞ ph¸ huû bªn trong t¨ng tõ 15 ÷ 20% ®Õn 30 ÷ 35%, tû sè gi÷a Ti vµ C kho¶ng 5,3 ÷ 6,5 th× tû lÖ phÕ phÈm Ýt h¬n so víi c¸c yÕu tè kh¸c). Tr−êng §¹i häc B¸ch khoa - §¹i häc §µ N½ng 98
Gi¸o tr×nh: Lý thuyÕt c¸n Gãc nghiªng cña trôc c¸n α vµ tèc ®é c¸n còng ¶nh h−ëng tíi l−îng Ðp tíi h¹n σ (h×nh 7.6). δ, % Qua h×nh 7.6, ta cã nhËn xÐt: c=0,37m/s 5 - Víi mét gãc α hîp lý, ta cã c=0,74m/s l−îng Ðp tíi h¹n cùc ®¹i, nghÜa lµ sù 4 ph¸ huû ë t©m Ýt nhÊt, tèc ®é quay 3 c=1,1m/s cµng nhá th× σ cµng cao. - Khi t¨ng gãc nghiªng th× tèc 2 ®é biÕn d¹ng t¨ng lªn nh−ng ®ång 1 thêi còng lµm gi¶m l−îng Ðp tíi h¹n, 0 song khi α t¨ng th× chiÒu dµi vïng 2 3 4 5 6 7 α, ®é biÕn d¹ng l¹i nhá ®i v× thÕ mµ l−îng H×nh 7.6- Sù phô thuéc cña l−îng Ðp tíi h¹n t¨ng lªn. Tæng hîp c¶ hai Ðp tíi h¹n vµo gãc nghiªng cña yÕu tè trªn cho ta gi¶i thÝch ®−îc trôc c¸n vµ tèc ®é quay ®iÓm cùc ®¹i cña ®å thÞ 7.6. VÒ ®−êng kÝnh cña ph«i c¸n ¶nh h−ëng ®Õn l−îng Ðp tíi h¹n ®−îc thÓ hiÖn trªn h×nh 7.7. Qua sè liÖu thùc nghiÖm cho thÊy khi t¨ng ®−êng kÝnh ph«i th× t¶i träng trªn ph«i mang tÝnh tËp trung nhiÒu h¬n, møc ®é biÕn d¹ng kh«ng ®ång ®Òu trªn tiÕt diÖn ph«i t¨ng lªn, cho nªn øng suÊt kÐo còng t¨ng lªn. L−îng Ðp tíi h¹n khi c¸n ngang - nghiªng thÐp C cã thÓ x¸c ®Þnh theo c«ng thøc sau: −1,5 −1 −3 ⎛l ⎞ ⎛d ⎞ ⎛ t ⎞ ⎟ (%C ) −1 δ = 4,5.⎜ 1 ⎟ .⎜ z ⎟ .U − 0,1 .⎜ ⎜d ⎟ (7.49) ⎝ z⎠ ⎝ d ⎠ ⎝ 1000 ⎠ trong ®ã, l1: chiÒu dµi phÇn tr−íc cña vïng biÕn d¹ng. t: nhiÖt ®é c¸n δ, % 11 H×nh 7.7- Sù phô thuéc cña l−îng Ðp 10 tíi h¹n vµo ®−êng kÝnh ph«i, ®−êng kÝnh trôc c¸n trong ®iÒu kiÖn 9 t = 12000C, β > 4; C = 0,37 m/s 8 7 30 40 50 d,mm 0,15 0,20 0,25 d/D Tr−êng §¹i häc B¸ch khoa - §¹i häc §µ N½ng 99

CÓ THỂ BẠN MUỐN DOWNLOAD