CH NG I ƯƠ
CÁC KHÁI NI M C B N C A LÝ THUY T ĐỆ Ơ Ả Ủ Ế Ồ
THỊ
Lý thuy t đ th là m t lĩnh v c đã có t lâu và có nhi u ng d ng hi n đ i. Nh ng tế ồ ị ộ ự ừ ề ứ ụ ệ ạ ữ ư
t ng c b n c a lý thuy t đ th đ c đ xu t vào nh ng năm đ u c a th k 18ưở ơ ả ủ ế ồ ị ượ ề ấ ữ ầ ủ ế ỷ
b i nhà toán h c l i l c ng i Th y S Lenhard Eurler. Chính ông là ng i đã sở ọ ỗ ạ ườ ụ ỹ ườ ử
d ng đ th đ gi i bài toán n i ti ng v các cái c u thành ph Konigsberg.ụ ồ ị ể ả ổ ế ề ầ ở ố
Đ th đ c s d ng đ gi i các bài toán trong nhi u lĩnh v c khác nhau. Ch ng h n,ồ ị ượ ử ụ ể ả ề ự ẳ ạ
đ th có th s d ng đ xác đ nh các m ch vòng trong v n đ gi i tích m ch đi n.ồ ị ể ử ụ ể ị ạ ấ ề ả ạ ệ
Chúng ta có th phân bi t các h p ch t hóa h c h u c khác nhau v i cùng công th cể ệ ợ ấ ọ ữ ơ ớ ứ
phân t nh ng khác nhau v c u trúc phân t nh đ th . Chúng ta có th xác đ nh haiử ư ề ấ ử ờ ồ ị ể ị
máy tính trong m ng có th trao đ i thông tin đ c v i nhau hay không nh mô hìnhạ ể ổ ượ ớ ờ
đ th c a m ng máy tính. Đ th có tr ng s trên các c nh có th s d ng đ gi i cácồ ị ủ ạ ồ ị ọ ố ạ ể ử ụ ể ả
bài toán nh : Tìm đ ng đi ng n nh t gi a hai thành ph trong m ng giao thông.ư ườ ắ ấ ữ ố ạ
Chúng ta cũng còn s d ng đ th đ gi i các bài toán v l p l ch, th i khóa bi u, vàử ụ ồ ị ể ả ề ậ ị ờ ể
phân b t n s cho các tr m phát thanh và truy n hình…ố ầ ố ạ ề
1. Đ NH NGHĨA Đ THỊ Ồ Ị
Đ th là m t c u trúc r i r c bao g m các đ nh và các c nh n i các đ nh này. Chúng taồ ị ộ ấ ờ ạ ồ ỉ ạ ố ỉ
phân bi t các lo i đ th khác nhau b i ệ ạ ồ ị ở ki uể và s l ng ố ượ c nh n i hai đ nh nào đó c aạ ố ỉ ủ
đ th . Đ có th hình dung đ c t i sao l i c n đ n các lo i đ th khác nhau, chúngồ ị ể ể ượ ạ ạ ầ ế ạ ồ ị
ta s nêu ví d s d ng chúng đ mô t m t m ng máy tính. Gi s ta có m t m ngẽ ụ ử ụ ể ả ộ ạ ả ử ộ ạ
g m các máy tính và các kênh đi n tho i (g i t t là kênh tho i) n i các máy tính này.ồ ệ ạ ọ ắ ạ ố
Chúng ta có th bi u di n các v trí đ t náy tính b i các đi m và các kênh tho i n iể ể ễ ị ặ ở ể ạ ố
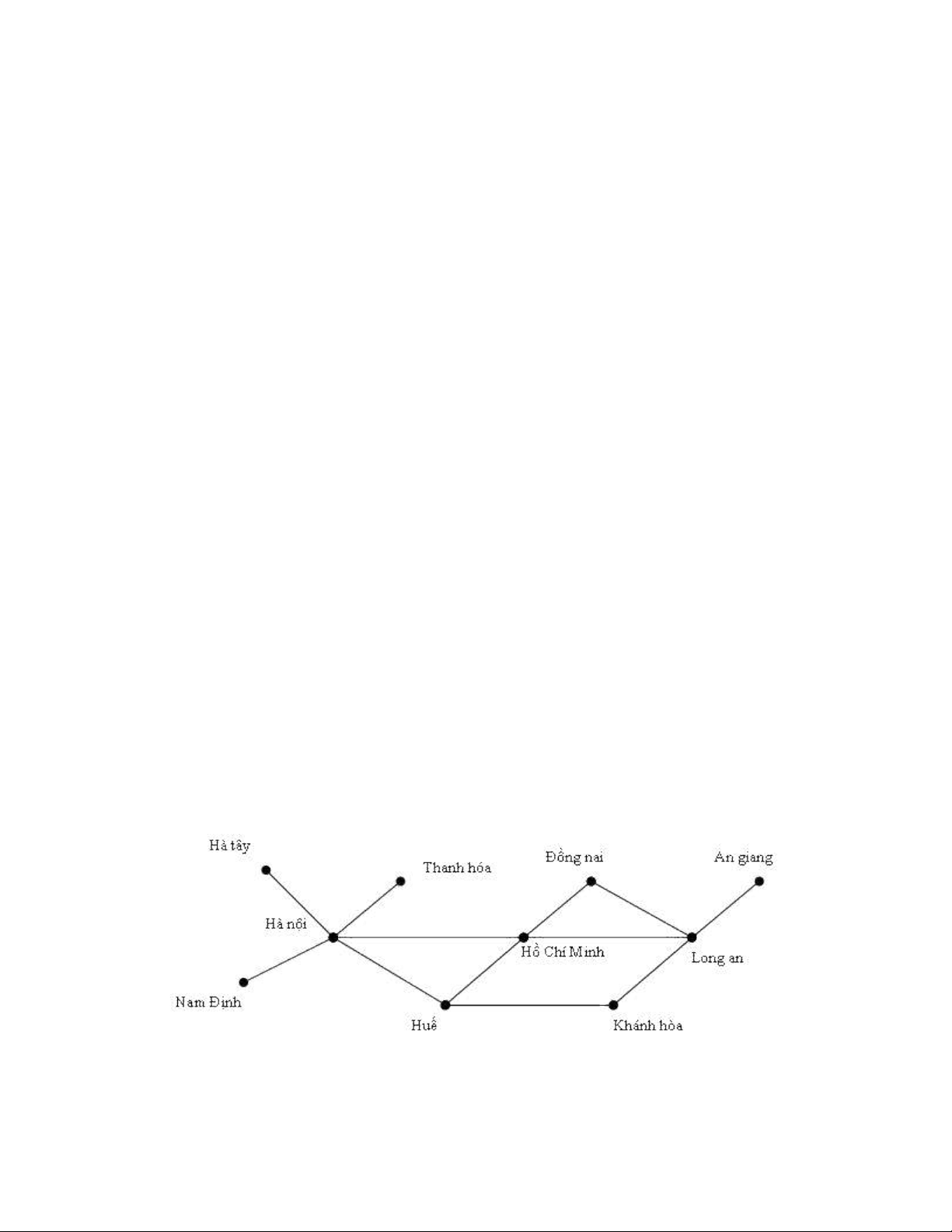
chúng b i các đo n n i, xem hình 1.ở ạ ố
Hình 1. S đ m ng máy tính.ơ ồ ạ
Nh n th y r ng trong m ng hình 1, gi a hai máy b t kỳ ch có nhi u nh t là m tậ ấ ằ ạ ở ữ ấ ỉ ề ấ ộ
kênh tho i n i chúng, kênh tho i naỳ cho phép liên l c c hai chi u và không có máyạ ố ạ ạ ả ề
tính nào l i đ c n i v i chính nó. S đ m ng máy cho trong hình 1 đ c g i là ạ ượ ố ớ ơ ồ ạ ượ ọ đ nơ
đ th vô h ngồ ị ướ . Ta đi đ n đ nh nghĩa sauế ị
Đ nh nghĩa 1.ị
Đ n đ th vô h ng G = (V,E) bao g m V là t p các đ nh, và E là t pơ ồ ị ướ ồ ậ ỉ ậ
các c p không có th t g m hai ph n t khác nhau c a V g i là cácặ ứ ự ồ ầ ử ủ ọ
c nh.ạ
Trong tr ng h p gi a hai máy tính nào đó th ng xuyên ph i truy n t i nhi uườ ợ ữ ườ ả ề ả ề
thông tin ng i ta ph i n i hai máy nàu b i nhi u kênh tho i. M ng v i đaườ ả ố ở ề ạ ạ ớ
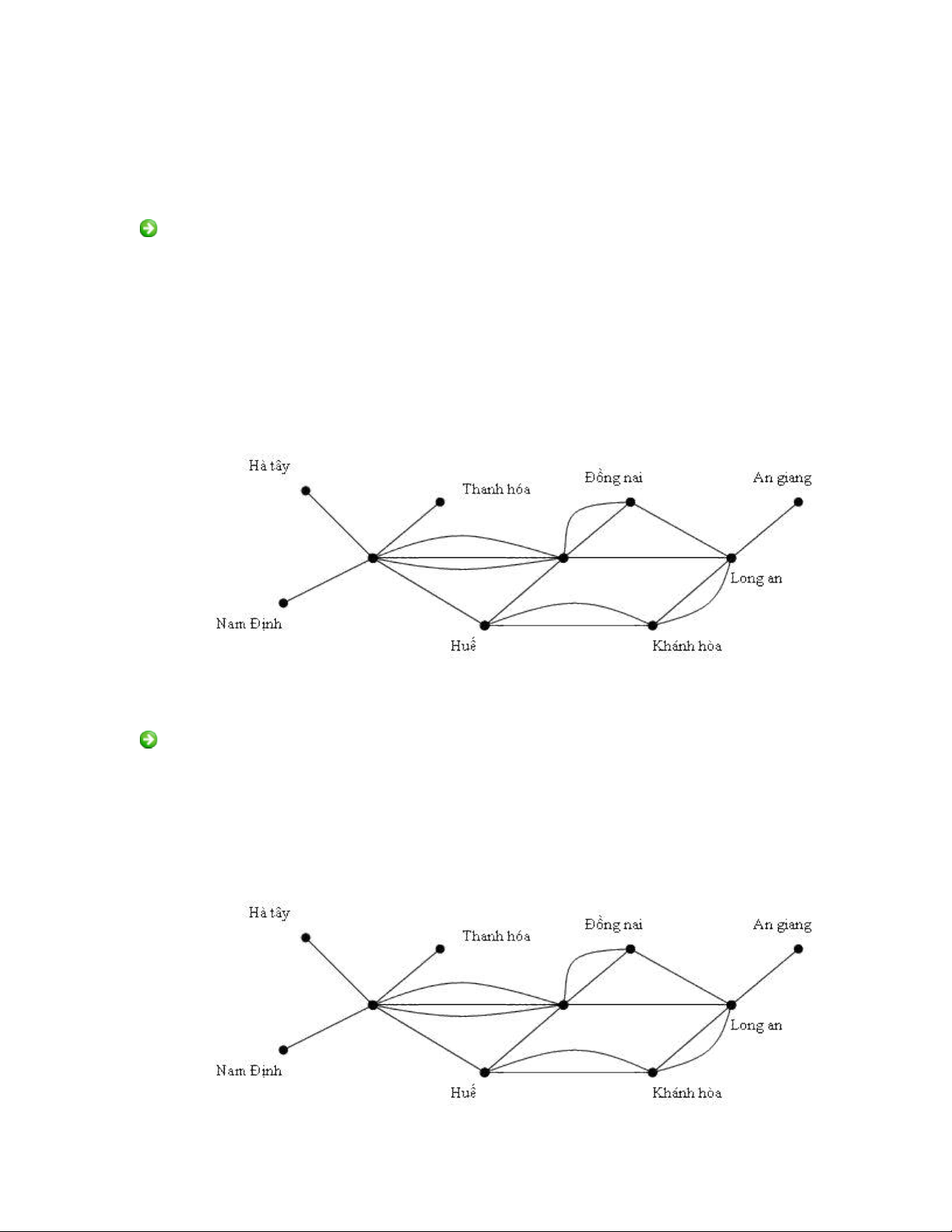
kênh tho i gi a các máy đ c cho trong hình 2.ạ ữ ượ
Hình 2. S đ m ng máy tính v i đa kênh tho i.ơ ồ ạ ớ ạ
Đ nh nghĩa 2.ị
Đa đ th vô h ng G= (V, E) bao g m V là t p các đ nh, và E là t pồ ị ướ ồ ậ ỉ ậ
các c p không có th t g m hai ph n t khác nhau c a V g i là cácặ ứ ự ồ ầ ử ủ ọ
c nh. Hai c nh eạ ạ 1 và e2 đ c g i là c nh l p n u chúng cùng t ngượ ọ ạ ặ ế ươ
ng v i m t c p đ nh.ứ ớ ộ ặ ỉ
Hình 3. S đ m ng máy tính v i kênh tho i thông báo.ơ ồ ạ ớ ạ
Rõ ràng m i đ n đ th đ u là đa đ th , nh ng không ph i đa đ th nào cũngỗ ơ ồ ị ề ồ ị ư ả ồ ị
là đ n đ th , vì trong đa đ th có th có hai (ho c nhi u h n) c nh n i m tơ ồ ị ồ ị ể ặ ề ơ ạ ố ộ
c p đ nh nào đó.ặ ỉ
Trong m ng máy tính có th có nh ng kênh tho i n i m t náy nào đó v i chínhạ ể ữ ạ ố ộ ớ
nó (ch ng h n v i m c đính thông báo). M ng nh v y đ c cho trong hình 3.ẳ ạ ờ ụ ạ ư ậ ượ
Khi đó đa đ th không th mô t đ c m ng nh v y, b i vì có nh ng ồ ị ể ả ượ ạ ư ậ ở ữ khuyên
(c nh n i m t đ nh v i chính nó). Trong tr ng h p nàychúng ta c n s d ngạ ố ộ ỉ ớ ườ ợ ầ ử ụ
đ n khái ni m ế ệ gi đ th vô h ng,ả ồ ị ướ đ c đ nh nghĩa nh sau:ượ ị ư
Đ nh nghĩa 3.ị
Gi đ th vô h ng G = (V, E) bao g m V là t p các đ nh và E là t pả ồ ị ướ ồ ậ ỉ ậ
các c p không có th t g m hai ph n t (không nh t thi t ph i khácặ ứ ự ồ ầ ử ấ ế ả
nhau) c a V g i là c nh. C nh e đ c g i là khuyên n u nó có d ng eủ ọ ạ ạ ượ ọ ế ạ
= (u, u).
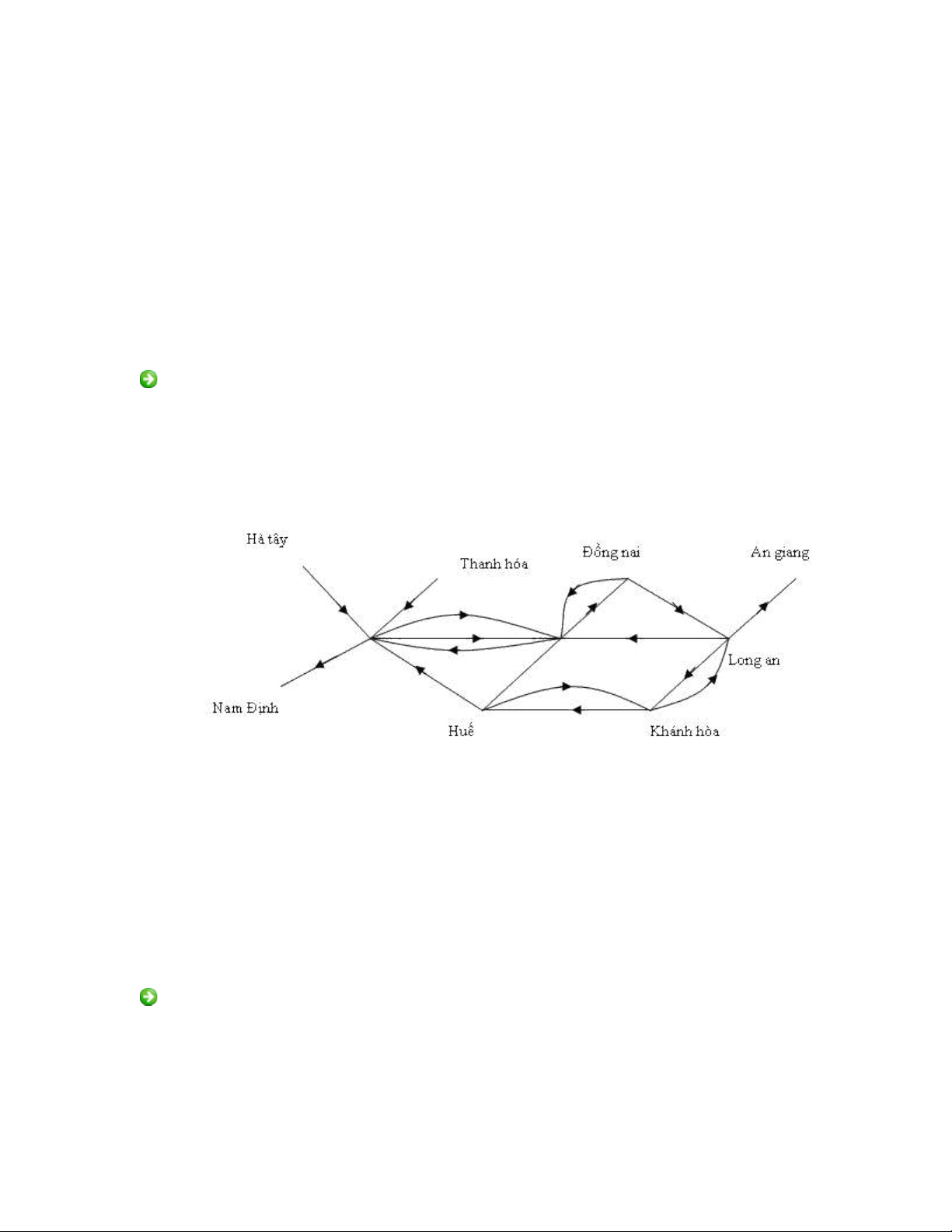
Hình 4. M ng máy tính v i kênh tho i m t chi uạ ớ ạ ộ ề
Các kênh tho i trong m ng máy tính có th ch cho phép truy n tin theo m tạ ạ ể ỉ ề ộ
chi u. Ch ng h n, trong hình 4 máy ch Hà N i ch có th nh n tin t cácề ẳ ạ ủ ở ộ ỉ ể ậ ừ
máy đ a ph ng, có m t s máy ch có th g i tin đi, còn các kênh tho i choở ị ươ ộ ố ỉ ể ử ạ
phép truy n tin theo c hai chi u đ c thay th b i hai c nh có h ng ng cề ả ề ượ ế ở ạ ướ ượ
chi u nhau.ề
Ta đi đ n đ nh nghĩa sau.ế ị
Đ nh nghĩa 4.ị
Đ n đ th có h ng G = (V, E) bao g m V là t p các đ nh và E là t pơ ồ ị ướ ồ ậ ỉ ậ
các c p có th t g m hai ph n t khác nhau c a V g i là các cung.ặ ứ ự ồ ầ ử ủ ọ
N u trong m ng có th có đa kênh tho i m t chi u, ta s ph i s d ng đ nế ạ ể ạ ộ ề ẽ ả ử ụ ế
khái ni m ệđa đ th có h ngồ ị ướ :
Đ nh nghĩa 5.ị
Đa đ th có h ng G = (V, E) bao g m V là t p các đ nh và E là t pồ ị ướ ồ ậ ỉ ậ
các c p có th t g m hai ph n t khác nhau c a V g i là các cung.ặ ứ ự ồ ầ ử ủ ọ
Hai cung e1, e2 t ng ng v i cùng m t c p đ nh đ c g i là cung l p.ươ ứ ớ ộ ặ ỉ ượ ọ ặ
Trong các ph n ti p theo ch y u chúng ta s làm vi c v?i đ n đ th vô h ngầ ế ủ ế ẽ ệ ơ ồ ị ướ
và đ n đ th có h ng. Vì v y, đ cho ng n g n, ta s b qua tính t ơ ồ ị ướ ậ ể ắ ọ ẽ ỏ ừ đ n ơkhi
nh c đ n chúng.ắ ế
2. CÁC THU T NG C B NẬ Ữ Ơ Ả
Trong m c này chúng ta s trình bày m t s thu t ng c b n c a lý thuy t đ th .ụ ẽ ộ ố ậ ữ ơ ả ủ ế ồ ị
Tr c tiên, ta xét các thu t ng mô t các đ nh và c nh c a đ th vô h ng.ướ ậ ữ ả ỉ ạ ủ ồ ị ướ
Đ nh nghĩa 1. ị
Hai đ nh u và v c a đ th vô h ng G đ c g i là k nhau n u (u,v) là c nhỉ ủ ồ ị ướ ượ ọ ề ế ạ
c a đ th G. N u e = (u, v) là c nh c a đ th ta nói c nh này là liên thu c v iủ ồ ị ế ạ ủ ồ ị ạ ộ ớ
hai đ nh u và v, ho c cũng nói là n i đ nh u và đ nh v, đ ng th i các đ nh u và vỉ ặ ố ỉ ỉ ồ ờ ỉ
s đ c g i là các đ nh đ u c a c nh (u, v).ẽ ượ ọ ỉ ầ ủ ạ
Đ có th bi t có vao nhiêu c nh liên thu c v i m t đ nh, ta đ a vào đ nh nghĩa sauể ể ế ạ ộ ớ ộ ỉ ư ị
Đ nh nghĩa 2. ị
Ta g i b c c a đ nh v trong đ th vô h ng là s c nh liên thu c v i nó và sọ ậ ủ ỉ ồ ị ướ ố ạ ộ ớ ẽ
ký hi u là deg(v).ệ
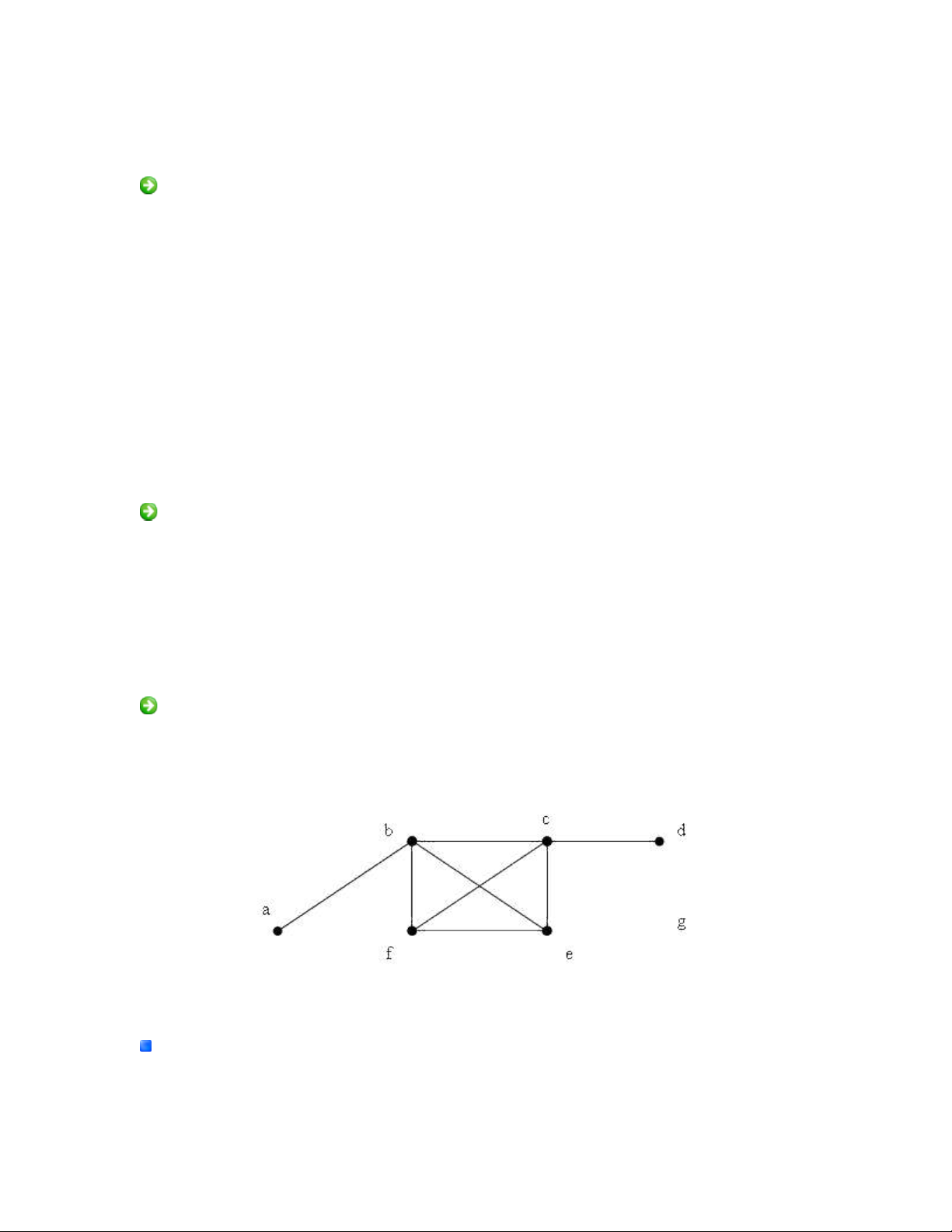
Hình 1. Đ th vô h ngồ ị ướ
Thí d 1.ụ Xét đ th cho trong hình 1, ta có ồ ị
deg(a) = 1, deg(b) = 4, deg(c) = 4, deg(f) = 3,
deg(d) = 1, deg(e) = 3, deg(g) = 0
Đ nh b c 0 g i là ỉ ậ ọ đ nh cô l pỉ ậ . Đ nh b c 1 đ c g i là đ nh treo. Trong ví d trên đ nh gỉ ậ ượ ọ ỉ ụ ỉ
là đ nh cô l p, a và d là các đ nh treo. B c c a đ nh có tính ch t sau:ỉ ậ ỉ ậ ủ ỉ ấ
Đ nh lý 1. ịGi s G = (V, E) là đ th vô h ng v i m c nh. Khi đó tông b c c a t tả ử ồ ị ướ ớ ạ ậ ủ ấ
c các đ nh b ng hai l n s cung.ả ỉ ằ ầ ố
Ch ng minh.ứ Rõ ràng m i c nh e = (u, v) đ c tính m t l n trong ỗ ạ ượ ộ ầ deg(u) và
m t l n trong ộ ầ deg(v). T đó suy ra t ng t t c các b c c a các đ nh b ng haiừ ổ ấ ả ậ ủ ỉ ằ
l n s c nh.ầ ố ạ
Thí d 2. ụĐ th v i n đ nh có b c là 6 có bao nhiêu c nh?ồ ị ớ ỉ ậ ạ
Gi iả: Theo đ nh lý 1 ta có ị2m = 6n. T đó suy ra t ng các c nh c a đ th là 3n.ừ ổ ạ ủ ồ ị
H qu . ệ ả Trong đ th vô h ng, s đ nh b c l (nghĩa là có b c là s l ) là m t sồ ị ướ ố ỉ ậ ẻ ậ ố ẻ ộ ố
ch n.ẵ
Ch ng minh.ứ Th c v y, g i O và U t ng ng là t p đ nh b c l và t p đ nhự ậ ọ ươ ứ ậ ỉ ậ ẻ ậ ỉ
b c ch n c a đ th . Ta cóậ ẵ ủ ồ ị
2m = å deg(v) + å deg(v)
vÎ U vÎ O
Do deg(v) là ch n v i v là đ nh trong U nên t ng th nh t trên là s ch n. Tẵ ớ ỉ ổ ứ ấ ở ố ẵ ừ
đó suy ra t ng th hai (chính là t ng b c c a các đ nh b c l ) cũng ph i là sổ ứ ổ ậ ủ ỉ ậ ẻ ả ố
ch n, do t t c các s h ng c a nó là s l , nên t ng này ph i g m m t sẵ ấ ả ố ạ ủ ố ẻ ổ ả ồ ộ ố
ch n các s h ng. Vì v y, s đ nh b c l ph i là s ch n.ẵ ố ạ ậ ố ỉ ậ ẻ ả ố ẵ
Ta xét các thu t ng t ng t cho đ th vô h ng.ậ ữ ươ ự ồ ị ướ
Đ nh nghĩa 3.ị
N u e = (u, v) là cung c a đ th có h ng G thì ta nói hai đ nh u và v là kế ủ ồ ị ướ ỉ ề
nhau, và nói cung (u, v) n i đ nh u v i đ nh v ho c cũng nói cung này là đi raố ỉ ớ ỉ ặ
kh i đ nh u và vào đ nh v. Đ nh u(v) s đ c g là đ nh đ u (cu i) c a cungỏ ỉ ỉ ỉ ẽ ượ ị ỉ ầ ố ủ
(u,v).
T ng t nh khái ni m b c, đ i v i đ th có h ng ta có khái ni m bán b c ra vàươ ự ư ệ ậ ố ớ ồ ị ướ ệ ậ
bán b c vào c a m t đ nh.ậ ủ ộ ỉ
Đ nh nghĩa 4.ị
Ta g i bán b c ra (bán b c vào) c a đ nh v trong đ th có h ng là s cungọ ậ ậ ủ ỉ ồ ị ướ ố
c a đ th đi ra kh i nó (đi vào nó) và ký hi u là degủ ồ ị ỏ ệ +(v) (deg-(v))