CHÖÔNG 1
ÑIEÀU BIEÂN (AM: Amplitude modulation)
I. Phoå cuûa tín hieäu ñieàu bieân:
Ñieàu bieân laø quaù trình laøm cho bieân ñoä taûi tin bieán ñoåi theo tin töùc.
Giaû thieát tin töùc laø tín hieäu aâm taàn coù phaïm vi bieán ñoåi taàn soá töø minmax,
ta coù:
V = V.cost (1.1)
Taûi tin laø dao ñoäng cao taàn:
Vo = V0.cos0t (1.2)
Töø (1-1) vaø (1-2) ta ñöôïc tín hieäu ñieàu bieân coù daïng:
3.1tcostcosm1V
tcostcos
V
V
1V
tcostcosVVtV
00
0
0
0
00AM
Trong ñoù:
0
V
V
m
laø heä soá ñieàu cheá hay coøn goïi laø ñoä saâu ñieàu cheá. Heä soá
ñieàu cheá “m” phaûi thoûa maõn ñieàu kieän m 1. Neáu m > 1 thì maïch coù hieän töôïng
ñieàu cheá vaø tín hieäu meùo traàm troïng (hình 1-1).
Trong thöïc teá mmax = 0,7 0,8 ñeå ñaûm baûo thu tín hieäu khoâng bò meùo. Ta
xaùc ñònh “m” trong thöïc teá baèng caùch ño caùc giaù trò Vmax, Vmin vaø aùp duïng coâng
thöùc:
4.1
VV
VV
2
VV
2
VV
V
V
m
minmax
minmax
minmax
minmax
0
Click to buy NOW!
P
D
F
-
X
C
h
a
n
g
e
V
i
e
w
e
r
w
w
w
.
d
o
c
u
-
t
r
a
c
k
.
c
o
m
Click to buy NOW!
P
D
F
-
X
C
h
a
n
g
e
V
i
e
w
e
r
w
w
w
.
d
o
c
u
-
t
r
a
c
k
.
c
o
m
Giáo trình phân tích tín hiệu điều biên và quan
hệ năng lượng trong tín hiệu điều biên với hệ
số phi tuyến
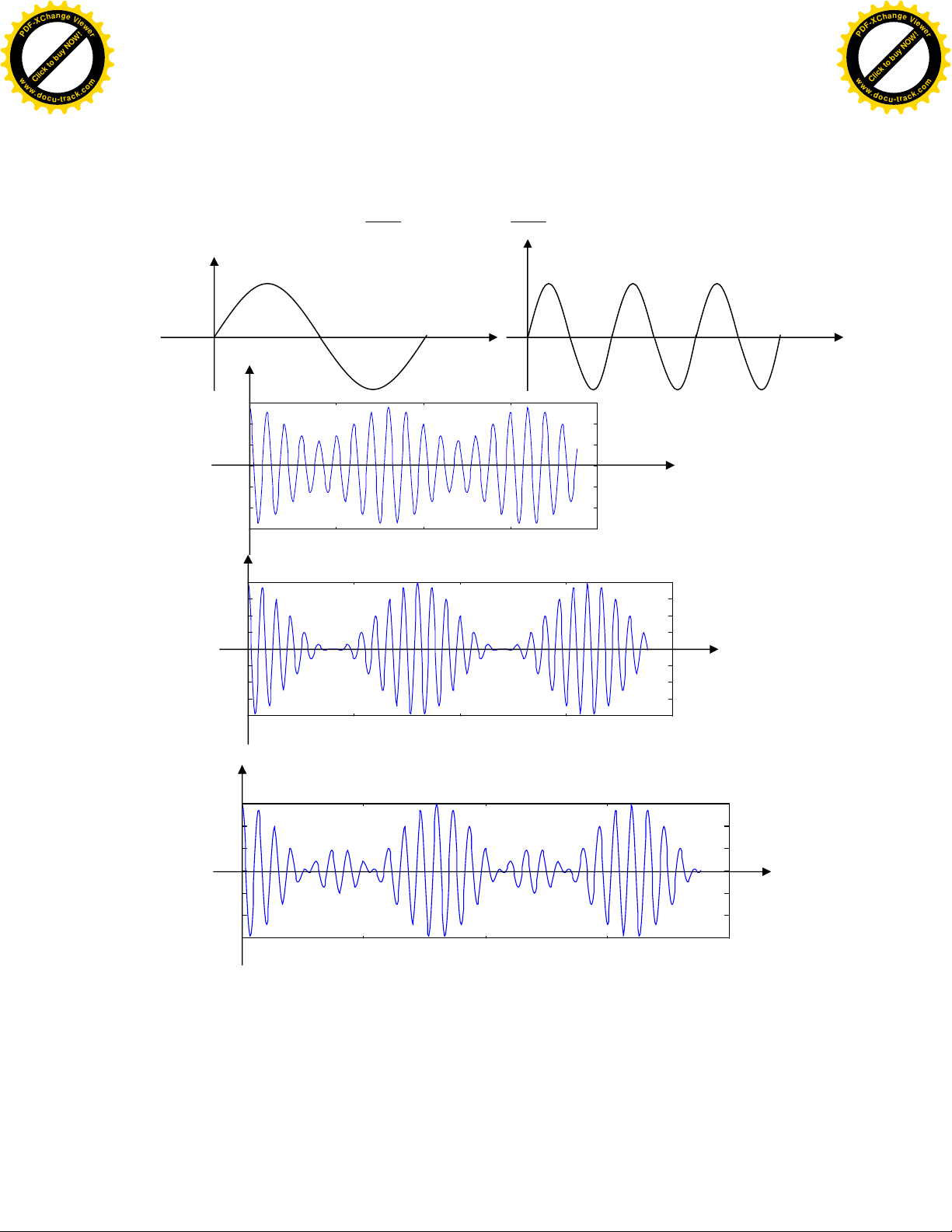
Khi m = 1 ta coù Vmax = 2V0 vaø Vmin = 0.
Bieán ñoåi löôïng giaùc coâng thöùc (1.3) ta coù:
5.1tcos
2
mV
tcos
mV
tcosVV 0
0
0
0
00AM
V
0
t
0
t
V
0
0 5 1 0 1 5 2 0
- 3
- 2
- 1
0
1
2
3
t
V
AM
m < 1
0 5 1 0 1 5 2 0
- 4
- 3
- 2
- 1
0
1
2
3
4
t
VAM
m = 1
0 5 1 0 1 5 2 0
- 6
- 4
- 2
0
2
4
6
t
VAM
m > 1
Hình 1.1 Daïng tín
hieäu V
, V
0
vaø tín hieäu ñieàu bieân V
AM
Click to buy NOW!
P
D
F
-
X
C
h
a
n
g
e
V
i
e
w
e
r
w
w
w
.
d
o
c
u
-
t
r
a
c
k
.
c
o
m
Click to buy NOW!
P
D
F
-
X
C
h
a
n
g
e
V
i
e
w
e
r
w
w
w
.
d
o
c
u
-
t
r
a
c
k
.
c
o
m
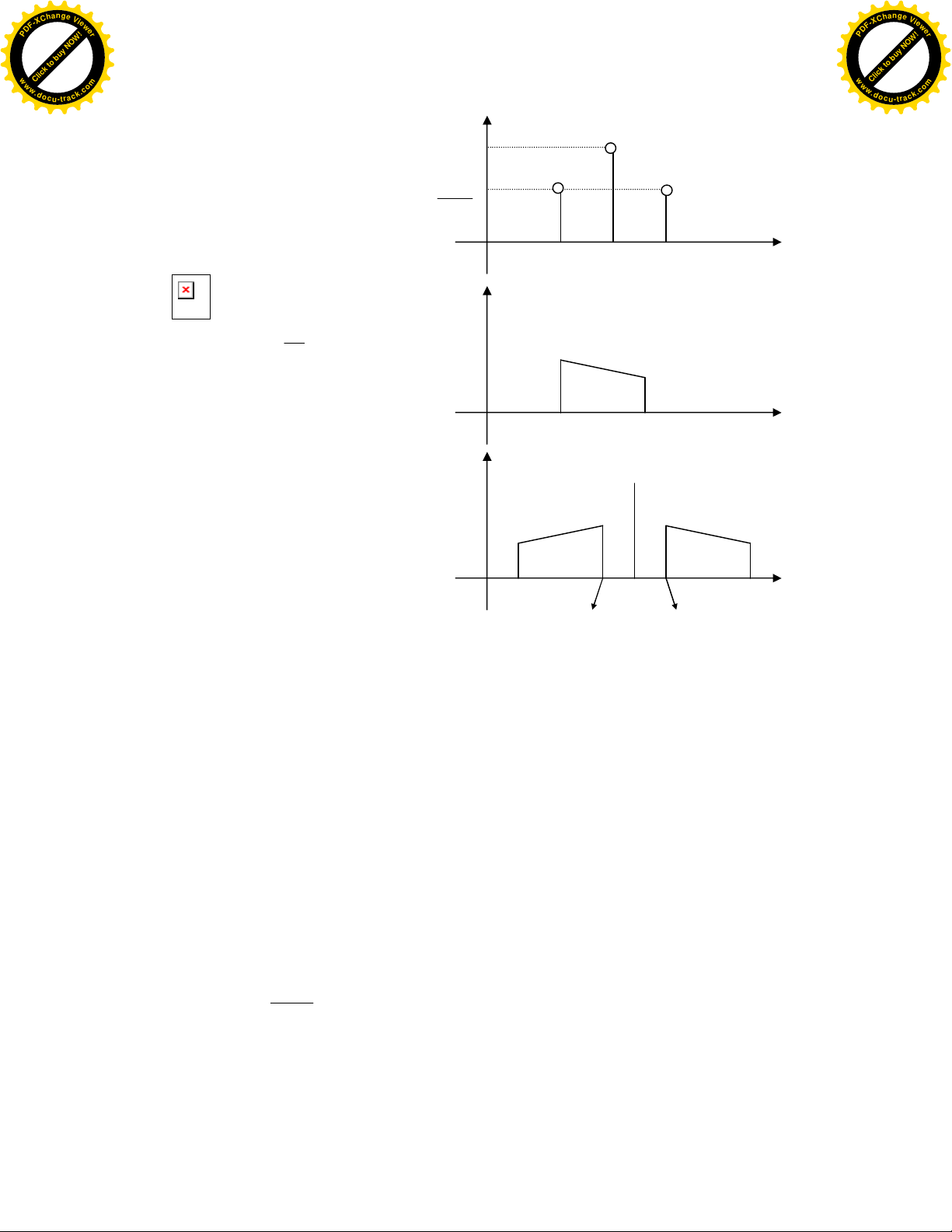
Nhö vaäy khi ñieàu
cheá ñôn aâm phoå cuûa tín
hieäu ñieàu bieân AM coù ba
thaønh phaàn: Taûi tin coù taàn
soá 0 vaø coù bieân ñoä V0;
hai dao ñoäng bieân coù taàn
soá 0 vaø coù bieân ñoä
nhö hình 1-2,a. Khi
m=1 thì
2
V
V0
AM
Neáu ta ñieàu cheá
moät daõi aâm taàn
(minmax) vaøo taûi tin, ta
seõ coù phoå cuûa tín hieäu AM
nhö hình 1-2,c.
Ta thaáy ngoaøi taûi
tin 0 coù bieân ñoä V0 coøn
coù hai bieân taàn: bieân taàn
treân coù taàn soá töø (0 -
min) ñeán (0 + max) vaø
bieân taàn döôùi coù taàn soá töø
(0 - max) ñeán (0 + min)
ñoái xöùng qua taûi tin.
Thöïc chaát phoå cuûa caùc dao ñoäng hai bieân khoâng ñoàng ñieàu nhau maø caøng
xa 0 thì bieân ñoä caøng giaûm do ñaëc tuyeán loïc cuûa boä coäng höôûng khoâng phaûi laø
hình chöõ nhaät lyù töôûng.
II. Quan heä naêng löôïng trong ñieàu bieân:
Trong tín hieäu ñaõ ñieàu bieân, caùc bieân taàn chöùa tin töùc, coøn taûi tin khoâng
mang tin töùc. Nhö vaäy coâng suaát taûi tin laø coâng suaát tieâu hao voâ ích, coøn coâng suaát
bieân taàn laø coâng suaát höõu ích.
Coâng suaát taûi tin laø coâng suaát bình quaân trong moät chu kyø taûi tin:
Po = (1.6)
V
2
0
2RL
0
-
0
+
0
min max
0
-
max 0
+
max
0
0
-
min 0
+
min
0
0
0
Hình 1-2 Phoå cuûa rín hieäu AM
V
AM
V
mV0
V
0
Click to buy NOW!
P
D
F
-
X
C
h
a
n
g
e
V
i
e
w
e
r
w
w
w
.
d
o
c
u
-
t
r
a
c
k
.
c
o
m
Click to buy NOW!
P
D
F
-
X
C
h
a
n
g
e
V
i
e
w
e
r
w
w
w
.
d
o
c
u
-
t
r
a
c
k
.
c
o
m
Coâng suaát bieân taàn:
8.1
2
m
PPPP
7.1
2
m
P
R2
1
2
mV
PP
2
btbtbt
2
L
2
0
btbt
000
000
Khi ñieàu cheá saâu (100%): m = 1 thì
P
P0
bt
(1.9)
Töø (1.3) ta coù: VAmmax = V0(1+m)
Do ñoù:
2
L
2
2
0
maxAM m1P
R2
m1V
P
0
(1.10)
Khi m = 1 thì PAMmax = 4Po (1.11)
Vaäy coâng suaát trung bình trong moät chu kyø ñieàu cheá:
12.1
2
m
1P
2
m
PPPPP
2
btAM 0000
Neáu m = 1 thì PAM = 3/2 Po (1.13)
Pbt = 1/3 PAM (1.14)
Heä soá lôïi duïng coâng suaát:
15.1
1m
2
1
2
m
1P
2
mP
P
P
k
2
2
2
AM
bt
0
0
Khi ñieàu cheá saâu nhaát m = 1 thì
1
k coù nghóa laø coâng suaát höõu ích chæ
baèng moät phaàn ba toång coâng suaát phaùt ñi.
Click to buy NOW!
P
D
F
-
X
C
h
a
n
g
e
V
i
e
w
e
r
w
w
w
.
d
o
c
u
-
t
r
a
c
k
.
c
o
m
Click to buy NOW!
P
D
F
-
X
C
h
a
n
g
e
V
i
e
w
e
r
w
w
w
.
d
o
c
u
-
t
r
a
c
k
.
c
o
m
Trong thöïc teá ñeå tín hieäu khoâng meùo m = 0,7 0,8 thì
3
1
k. Ñaây chính laø
nhöôïc ñieåm cuûa tín hieäu AM so vôùi tín hieäu ñieàu bieân (SSB).
III. Caùc chæ tieâu cô baûn cuûa dao ñoäng ñaõ ñieàu bieân:
1. Heä soá meùo phi tuyeán:
Trong ñoù:
0
00
I
....II
k
2
3
2
2
I(t ns) (n 2) laø bieân ñoä caùc thaønh phaàn doøng ñieän öùng vôùi haøi baäc cao
cuûa tín hieäu ñieàu cheá;
I(t s) laø bieân ñoä caùc thaønh phaàn bieân taàn.
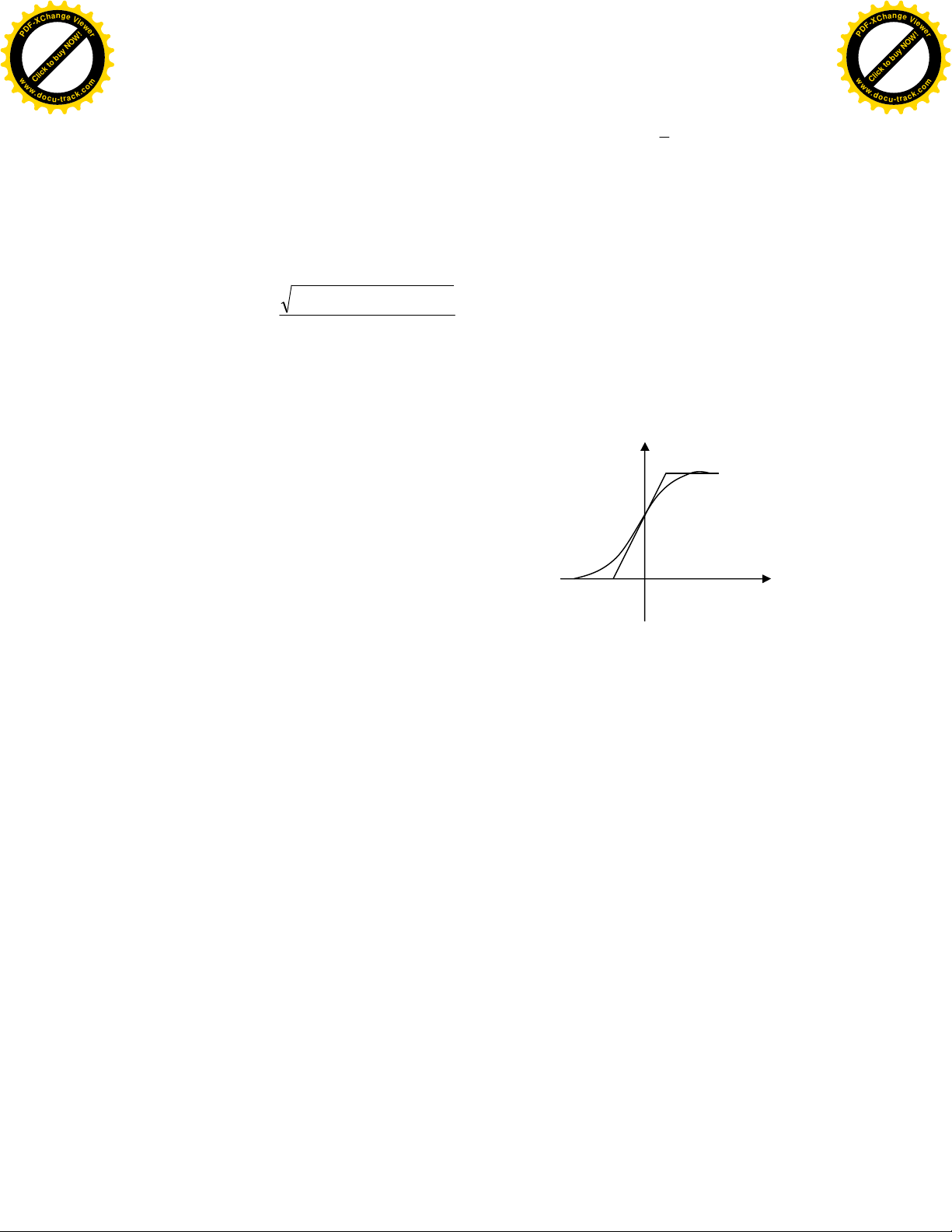
Ñeå ñaëc tröng cho meùo phi tuyeán
trong maïch ñieàu khieån, ngöôøi ta duøng
ñaëc tuyeán ñieàu cheá tónh (hình 1.3). Ñaëc
tuyeán ñieàu cheá tónh cho bieát quan heä
giöõa bieân ñoä tín hieäu ra vaø giaù trò töùc
thôøi cuûa tín hieäu ñieàu cheá ôû ñaàu vaøo.
Daïng toång quaùt cuûa ñaëc tuyeán
ñieàu cheá tónh ñöôïc bieåu dieãn treân hình
1-3.
Ñöôøng ñaëc tuyeán ñieàu cheá tónh lyù töôûng laø moät ñöôøng thaúng töø C ñeán A.
Ñaëc tuyeán ñieàu cheá tónh khoâng thaúng seõ laøm cho löôïng bieán ñoåi cuûa bieân ñoä dao
ñoäng cao taàn ñaàu ra so vôùi giaù trò ban ñaàu (ñieåm B) khoâng tyû leä ñöôøng thaúng vôùi
trò töùc thôøi cuûa ñieän aùp ñieàu cheá. Do ñoù treân ñaàu ra thieát bò ñieàu bieân, ngoaøi caùc
thaønh phaàn höõu ích (caùc bieân taàn), coøn coù caùc thaønh phaàn baäc cao khoâng mong
muoán khaùc. Trong ñoù ñaùng löu yù nhaát laø thaønh phaàn cuûa taàn soá t 2s coù theå loït
vaøo caùc bieân taàn maø khoâng theå loïc ñöôïc.
Ñeå giaûm meùo phi tuyeán, caàn haïn cheá phaïm vi laøm vieäc cuûa boä ñieàu cheá
trong ñoaïn ñöôøng thaúng cuûa ñaëc tuyeán ñieàu cheá tónh. Luùc ñoù buoäc phaûi giaûm ñoä
saâu ñieàu cheá.
A
B
C
U
I
0
Hình 1-3: Ñaëc tuyeán ñieàu cheá tónh.
A–Giaù trò cöïc ñaïi; B–Taûi tin chöa ñieàu cheá
Click to buy NOW!
P
D
F
-
X
C
h
a
n
g
e
V
i
e
w
e
r
w
w
w
.
d
o
c
u
-
t
r
a
c
k
.
c
o
m
Click to buy NOW!
P
D
F
-
X
C
h
a
n
g
e
V
i
e
w
e
r
w
w
w
.
d
o
c
u
-
t
r
a
c
k
.
c
o
m