Chương 4
Ước lượng tham số
Ước lượng tham số là một trong những bài toán cơ bản của thống kê toán học. Khi
nghiên cứu một dấu hiệu đặc trưng dưới dạng các đặc tính định lượng (chẳng hạn
như chiều cao, cân nặng, độ dài, . . . ) của tổng thể thông qua biến ngẫu nhiên X,
nếu xác định được quy luật phân phối xác suất của Xthì việc đưa ra các đánh giá
cũng như các dự báo về sự biến động của tổng thể liên quan đến đặc tính này sẽ
chính xác và khách quan. Tuy nhiên không phải lúc nào chúng ta cũng xác định
được quy luật phân phối xác suất của X. Trong một số trường hợp, bằng phương
pháp phân tích lý thuyết ta có thể biết được dạng toán học của hàm phân phối
hoặc hàm mật độ của X. Tuy nhiên, các tham số đặc trưng của nó như kỳ vọng,
phương sai, hoặc tỷ lệ . . . (gọi chung là tham số θ) lại chưa biết nên ta cần phải xác
định θ. Việc tính chính xác θlà khó có thể thực hiện được mà ta chỉ có thể tính gần
đúng. Việc tính gần đúng tham số đặc trưng θthông qua mẫu cụ thể đã có gọi là
ước lượng tham số (estimate for parameters).
Chương này sẽ trình bày bài toán ước lượng tham số cho kỳ vọng toán và tỷ lệ.
Mục 4.1 sẽ giới thiệu phương pháp ước lượng điểm làm cơ sở quan trọng cho việc
giải quyết bài toán ước lượng bằng khoảng tin cậy được trình bày trong Mục 4.2.
Nội dung của chương được tham khảo chủ yếu từ các tài liệu [2], [6]-[8], [10] và [12].
4.1. Phương pháp ước lượng điểm
Bài toán. Xét biến ngẫu nhiên Xcủa một tổng thể mà ta đã biết quy luật phân
phối xác suất nhưng chưa biết tham số đặc trưng θcủa X. Hãy ước lượng θvới độ
tin cậy cho trước 1−α.
Phương pháp chung. Từ tổng thể cần nghiên cứu rút ra một mẫu ngẫu nhiên
kích thước nvà dựa vào mẫu đó mà xây dựng một thống kê G dùng để ước lượng θ.
Phương pháp ước lượng điểm (point estimation) chủ trương dùng một giá trị để
thay thế cho tham số θchưa biết về tổng thể, vì bản thân θlà một số xác định.
Thông thường giá trị được chọn là một thống kê Gnào đó của mẫu ngẫu nhiên. Có
nhiều cách chọn thống kê Gkhác nhau tạo nên những phương pháp ước lượng điểm
khác nhau.
97
98 Chương 4: Ước lượng tham số
Giả sử cần ước lượng tham số θcủa biến ngẫu nhiên X. Đối với phương pháp
ước lượng điểm ta có thể tiến hành theo các bước như sau:
•Bước 1. Từ tổng thể lập mẫu ngẫu nhiên kích thước n:W= (X1,X2, . . . ,Xn).
•Bước 2. Lập thống kê G=f(X1,X2, . . . ,Xn)được gọi là hàm ước lượng của
θ. Thông thường chọn thống kê mẫu tương ứng với tham số θcần ước lượng,
chẳng hạn, để ước lượng kì vọng toán E(X)của biến ngẫu nhiên Xthì người
ta thường chọn thống kê là trung bình mẫu X, để ước lượng phương sai V(X),
chọn thống kê là phương sai điều chỉnh mẫu S′2.
•Bước 3. Xác định mẫu cụ thể và tính được giá trị g=f(x1,x2, . . . , xn)của
thống kê Gtrên mẫu cụ thể đó. Từ đó suy ra ước lượng của θlà giá trị gvừa
tính được.
Chất lượng của ước lượng không thể đánh giá qua một giá trị cụ thể của Gvì
như vậy chỉ có cách so sánh trực tiếp gvà θmà θlại chưa biết. Do đó chỉ có thể đánh
giá chất lượng của ước lượng thông qua bản thân thống kê G=f(X1,X2, . . . ,Xn).
Rõ ràng là có vô số cách chọn hàm f, tức là có vô số thống kê Gcó thể dùng làm
ước lượng của θnên cần đưa ra một tiêu chuẩn để đánh giá chất lượng thống kê G,
từ đó lựa chọn được thống kê “xấp xỉ một cách tốt nhất” tham số ước lượng. Có 3
tiêu chuẩn cơ bản để chọn thống kê như sau.
Định nghĩa 4.1.1. Thống kê Gcủa mẫu được gọi là
(i) ước lượng không chệch của tham số θcủa biến ngẫu nhiên Xnếu E(G) = θ.
Ngược lại, nếu E(G)=θthì Gđược gọi là ước lượng chệch của θ.
(ii) ước lượng hiệu quả của tham số θcủa biến ngẫu nhiên Xnếu nó là ước lượng
không chệch và có phương sai nhỏ nhất so với mọi ước lượng không chệch khác
được xây dựng trên cùng một mẫu.
(iii) ước lượng vững của tham số θcủa biến ngẫu nhiên Xnếu Ghội tụ theo xác
suất đến θkhi n→ ∞, tức là với mọi εdương bé tùy ý ta luôn có lim
x→∞P(|G−
θ|< ε) = 1.
Chú ý 4.1.2. (i) Glà ước lượng không chệch của tham số θkhông có nghĩa là mọi
giá trị của Gđều trùng khít với θmà chỉ có nghĩa là trung bình các giá trị của thống
kê Gbằng θ. Từng giá trị của Gcó thể sai lệch rất lớn so với θ.
(ii) Trung bình mẫu Xlà ước lượng không chệch của kỳ vọng của biến ngẫu
nhiên X, nghĩa là E(X) = E(X). Trung bình mẫu Xcũng là ước lượng hiệu quả
(vững) của E(X).
(iii) Tần suất mẫu flà ước lượng không chệch của xác suất Pcủa biến ngẫu
nhiên X, nghĩa là E(f) = P. Tần suất mẫu flà ước lượng hiệu quả (vững) của xác
suất P.
(iv) Phương sai điều chỉnh mẫu S′2là ước lượng không chệch của phương sai
V(X)của biến ngẫu nhiên X, tức là E(S′2) = V(X). Phương sai điều chỉnh mẫu
S′2cũng là ước lượng hiệu quả (vững) của phương sai V(X).
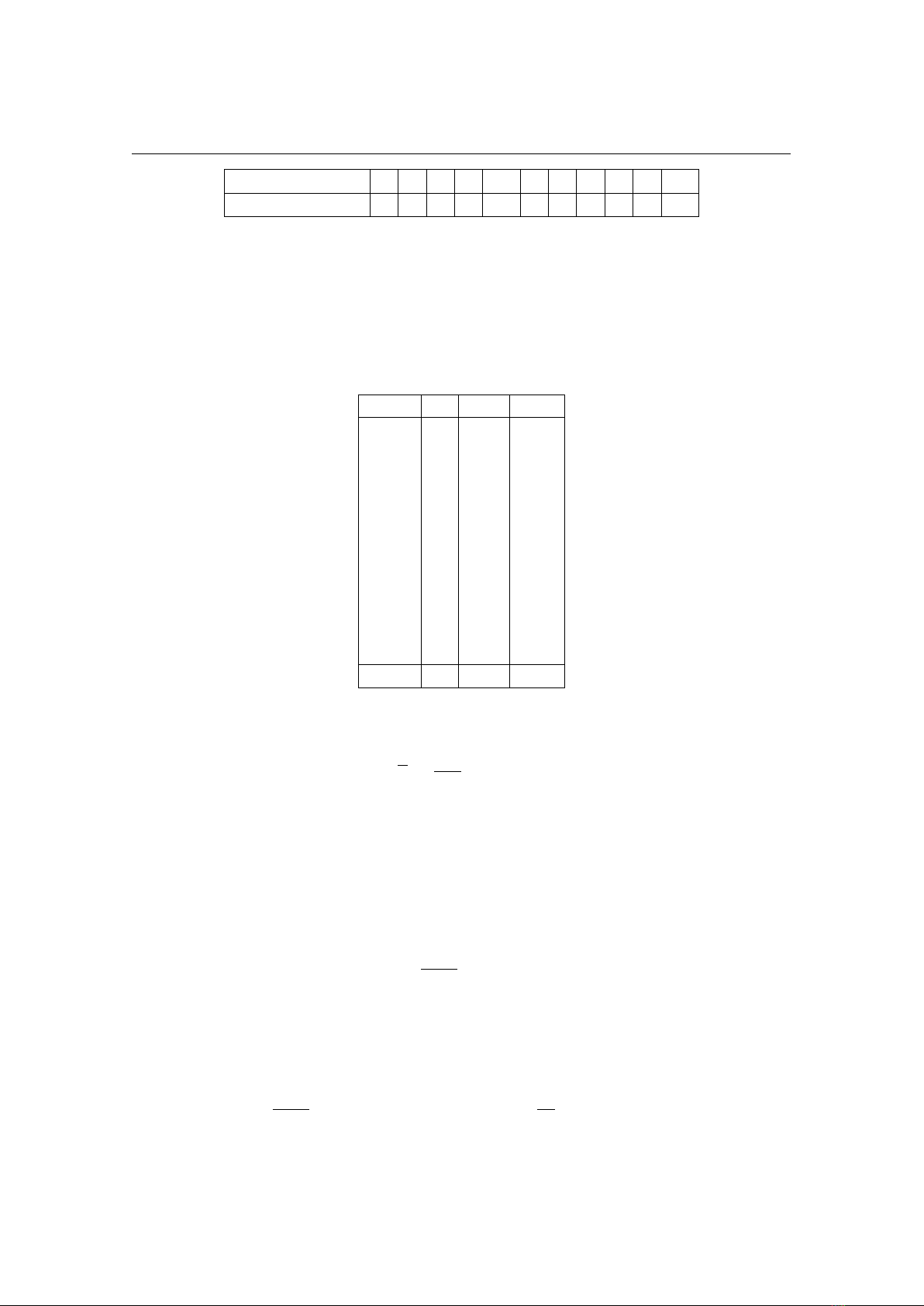
Ví dụ 4.1.3 Giả sử một lô hàng của một nhà máy đã được đóng thùng, mỗi thùng
50 sản phẩm. Kiểm tra ngẫu nhiên số phế phẩm trong 50 thùng hàng ta thu được
kết quả như sau:
4.1 Phương pháp ước lượng điểm 99
Số phế phẩm X0 1 2 3 4 5 6 7 8 9 10
Số thùng (ni) 0 2 3 7 20 6 4 7 2 1 1
(i) Hãy ước lượng cho số phế phẩm trung bình trong mỗi thùng.
(ii) Hãy ước lượng cho tỷ lệ phế phẩm của lô hàng đó.
(iii) Tìm ước lượng không chệch cho phương sai của số phế phẩm ở mỗi thùng.
Giải. (i) Gọi Xlà biến ngẫu nhiên chỉ số phế phẩm ở mỗi thùng. Đây là bài toán
ước lượng điểm cho kỳ vọng của tổng thể. Ta sẽ dùng trung bình mẫu để ước lượng
số phế phẩm trung bình trong mỗi thùng.
nixinixinix2
i
0 0 0 0
2 1 2 2
3 2 6 12
7 3 21 63
20 4 80 320
6 5 30 150
4 6 24 144
7 7 49 343
2 8 16 128
1 9 9 81
1 10 10 100
∑50 247 1343
Nhìn vào bảng trên ta thấy:
x=247
50 = 4,94.
Vậy số phế phẩm trung bình ở mỗi thùng hàng là khoảng 5sản phẩm.
(ii) Đây là bài toán ước lượng tỷ lệ của một tổng thể. Ta dùng tần suất mẫu (tỷ
lệ phế phẩm của 50 thùng hàng) để ước lượng tỷ lệ phế phẩm của cả lô hàng đó.
Tổng số sản phẩm điều tra là n= (50)(50) = 2500.
Số phế phẩm phát hiện là 247. Do đó, tỷ lệ phế phẩm trong mẫu gồm 50 thùng
hàng là
f=247
2500 = 0,0908.
Vậy tỷ lệ phế phẩm của lô hàng là vào khoảng (0,0908)(100%) = 9,88%.
(iii) Ước lượng không chệch cho phương sai của số phế phẩm ở mỗi thùng chính
là phương sai điều chỉnh mẫu S′2. Ta có:
s2=1343
50 −(4,94)2= 2,4564 ⇒s′2=50
49(2,4564) = 2,507.
Vậy phương sai của số phế phẩm giữa các thùng là vào khoảng 2,507.
100 Chương 4: Ước lượng tham số
4.2. Phương pháp ước lượng bằng khoảng tin cậy
4.2.1. Khái niệm
Các phương pháp ước lượng điểm nói trên có một nhược điểm cơ bản là khi kích
thước mẫu nhỏ thì ước lượng điểm tìm được có thể sai lệch rất nhiều so với giá trị
của tham số cần ước lượng, tức là sai số của ước lượng có thể rất lớn. Mặt khác
dùng các phương pháp trên không thể đánh giá được khả năng mắc sai lầm khi
ước lượng bằng bao nhiêu. Do đó khi kích thước mẫu nhỏ người ta thường sử dụng
phương pháp ước lượng bằng khoảng tin cậy.
Định nghĩa 4.2.1. Khoảng (θ1,θ2)của thống kê Gđược gọi là khoảng tin cậy
(interval confidence) của tham số θvới độ tin cậy 1−αnếu P(θ1< θ < θ2) = 1−α.
Tham số 1−α=γđược gọi là độ tin cậy của ước lượng, αđược gọi là mức ý
nghĩa,θ1là cận trái (giá trị tối thiểu), θ2là cận phải (giá trị tối đa), còn I=|θ1−θ2|
là độ dài khoảng tin cậy,I/2là bán kính khoảng.
Để giải một bài toán ước lượng tham số bằng khoảng tin cậy, ta tiến hành các
bước chính như sau:
•Bước 1. Từ tổng thể lập mẫu ngẫu nhiên W= (X1,X2, . . . ,Xn).
•Bước 2. Chọn thống kê G=f(X1,X2, . . . ,Xn,θ)sao cho quy luật phân phối
xác suất của Ghoàn toàn xác định.
•Bước 3. Với độ tin cậy 1−αcho trước có thể tìm được cặp giá trị α1và α2
sao cho α1+α2=αvà tương đương với chúng tìm được cặp phân vị θ1=θα1
và θ2=θα2thỏa mãn điều kiện
P(G < θ1) = α1;P(G > θ2) = α2⇒P(θ1< G < θ2) = 1 −(α1+α2) = 1 −α.
Như vậy, với độ tin cậy (1 −α)ta đã xây dựng được khoảng tin cậy (θ1, θ2)
cho G. Bằng các phép biến đổi tương đương, công thức trên luôn đưa được về dạng
P(G1< θ < G2) = 1−α, với G1=f(X1,X2, . . . ,Xn,θ1)và G2=f(X1,X2, . . . ,Xn,θ2).
Đó chính là khoảng tin cậy cần tìm.
Chú ý 4.2.2. (i) Khi tiến hành một phép thử với mẫu ngẫu nhiên W= (X1,X2,
. . . ,Xn)ta thu được một mẫu cụ thể w= (x1,x2, . . . ,xn), do đó tính được giá trị
của θ1và θ2ứng với mẫu cụ thể. Khi đó có kết luận là qua mẫu cụ thể w, với độ
tin cậy 1−α, tham số θcủa biến ngẫu nhiên gốc Xsẽ nằm trong khoảng (θ1,θ2).
(ii) Với độ tin cậy 1−αcho trước ta có thể tìm được vô số cặp (θ1,θ2)thỏa mãn
điều kiện α1+α2=α. Vì thế có vô số khoảng tin cậy tương ứng với độ tin cậy
đã cho.
4.2.2. Ước lượng kỳ vọng toán
Trong mục này ta sẽ xét bài toán ước lượng kỳ vọng toán của biến ngẫu nhiên Xxét
trong hai trường hợp khi Xcó phân phối chuẩn và khi Xkhông có phân phối chuẩn.
4.2 Phương pháp ước lượng bằng khoảng tin cậy 101
1. Khi biến ngẫu nhiên Xcó phân phối chuẩn N(a,σ2)
Bài toán. Cho biến ngẫu nhiên Xcó phân phối chuẩn N(a,σ2)với kỳ vọng a
chưa biết và phương sai σ2có thể đã biết (chưa biết). Hãy ước lượng tham số kỳ vọng
avới độ tin cậy 1−α.
Giải.
Bước 1. Từ tổng thể lập một mẫu ngẫu nhiên W= (X1,X2, . . . ,Xn)kích thước n.
Các bước tiếp theo của việc giải bài toán trên phụ thuộc vào việc chọn thống kê
Gsao cho phù hợp với các điều kiện của bài toán. Ta xét hai trường hợp tùy thuộc
vào phương sai σ2của biến ngẫu nhiên Xđã biết hoặc chưa biết.
a. Đã biết phương sai σ2của biến ngẫu nhiên X
Bước 2. Chọn thống kê
G=U=(X−a)√n
σ,
trong đó Xlà trung bình mẫu. Khi đó, theo Định lý giới hạn trung tâm, ta có
thống kê Uxấp xỉ phân phối chuẩn hóa N(0,1). Với độ tin cậy 1−αcho trước tìm
được cặp giá trị α1và α2sao cho α1+α2=α. Từ đó tìm được hai phân vị chuẩn
là uα1và u1−α2thỏa mãn điều kiện
P(U < uα1) = α1;P(U > u1−α2) = α2.
Suy ra
P(uα1< U < u1−α2) = 1 −(α1+α2) = 1 −α.
Vì uα1=−u1−α1nên thay thống kê Uvào biểu thức trên, ta thu được
P(−u1−α1<(X−a)√n
σ< u1−α2)= 1 −α, hay
P(X−σ
√nu1−α2< a < X+σ
√nu1−α1)= 1 −α.
Bước 3. Kết luận: với độ tin cậy bằng (1 −α), tham số acủa biến ngẫu nhiên
Xsẽ nằm trong khoảng
(X−σ
√nu1−α2;X+σ
√nu1−α1).(4.1)
Từ công thức (4.1) , để xác định khoảng tin cậy của a, người ta thường xét các
trường hợp đặc biệt của khoảng tin cậy theo cách chọn α1và α2như sau.
Khoảng tin cậy đối xứng: Nếu α1=α2=α
2thì khoảng tin cậy của alà:
(X−σ
√nu1−α
2;X+σ
√nu1−α
2).(4.2)
Trong (4.2), đặt ε=σ
√nu1−α
2thì biểu thức có dạng (X−ε;X+ε),εđược gọi
là độ chính xác của ước lượng, nó phản ánh mức độ sai lệch của trung bình mẫu so
với trung bình tổng thể với độ tin cậy (1 −α)cho trước.