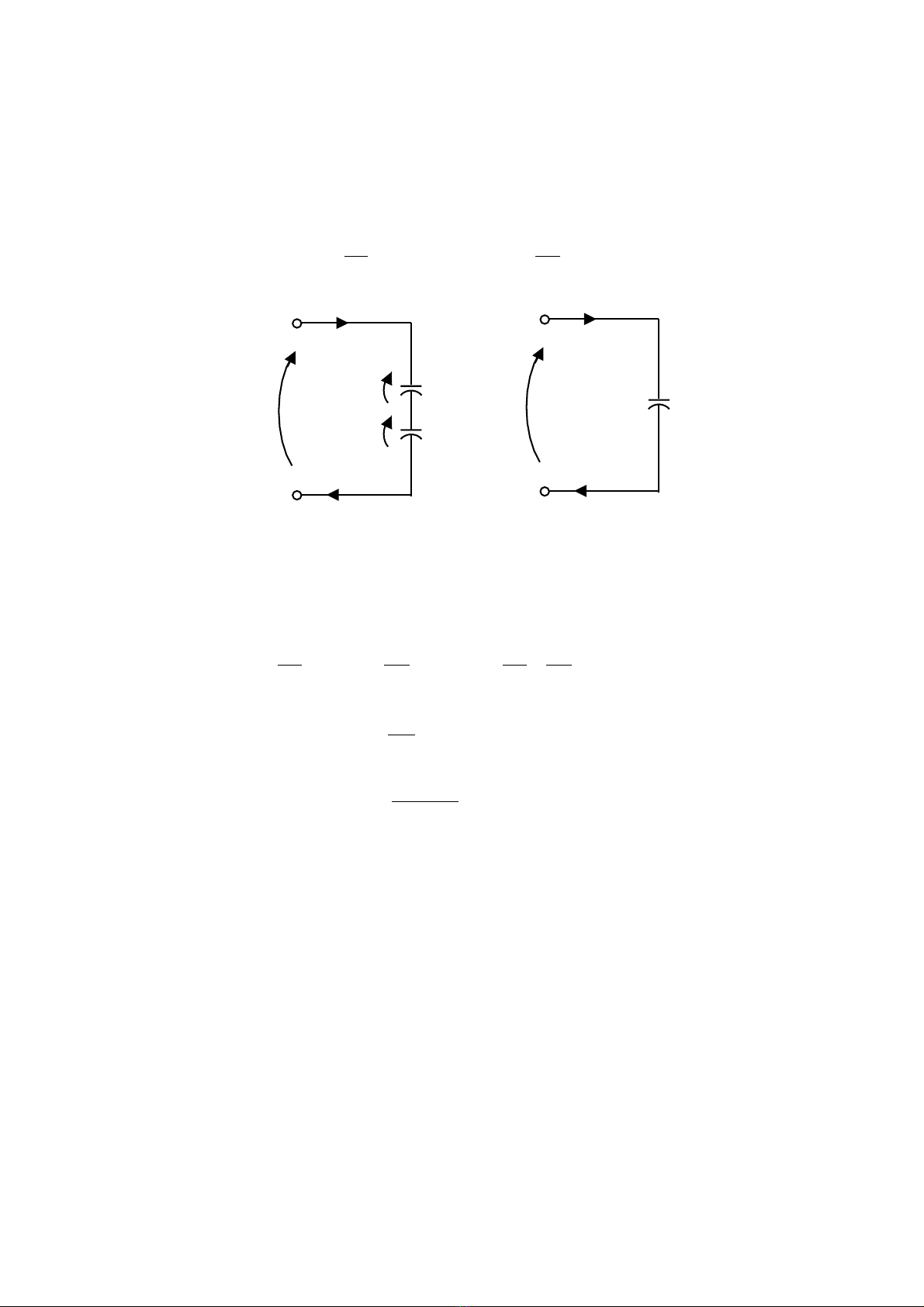
NÕu cã m¹ch thñy lùc nh− ë h×nh 2.2a, trong ®ã ¸p suÊt trªn ®−êng truyÒn cña m¹ch
lµ kh¸c nhau th× hÖ sè tÝch lòy ®µn håi t−¬ng ®−¬ng x¸c ®Þnh nh− d−íi ®©y.
Ph−¬ng tr×nh c©n b»ng ¸p suÊt :
P
A = P1 + P2 (2.5)
Theo (2.2) ta cã : ∫
=
t
0
T
1
1dt.Q.
C
1
P vµ ∫
=
t
0
T
2
2dt.Q.
C
1
P
QV
QT
47
QV
P
2
P
1
QT
C1pA
pACT
C2
b)
a)
H×nh 2.2. S¬ ®å m¹ch thñy lùc cã ¸p suÊt kh«ng b»ng nhau
a- S¬ ®å chi tiÕt; b- S¬ ®å t−¬ng ®−¬ng.
nªn : ∫∫∫ ⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛+=+=
t
0
T
21
t
0
T
2
t
0
T
1
Adt.Q.
C
1
C
1
dt.Q.
C
1
dt.Q.
C
1
P (2.6)
hay : ∫
=
t
0
T
T
Adt.Q.
C
1
P (2.7)
víi :
21
21
TCC
C.C
C+
=
CT ®−îc gäi lµ hÖ sè tÝch lòy ®µn håi t−¬ng ®−¬ng. S¬ ®å m¹ch thñy lùc ë h×nh 2.2a cã
thÓ thay thÕ b»ng s¬ ®å t−¬ng ®−¬ng nh− ë h×nh 2.2b.
2.2. Ph©n tÝch m¹ch thñy lùc khi c¶ hai buång cña xylanh
®Òu cã dÇu ®µn håi
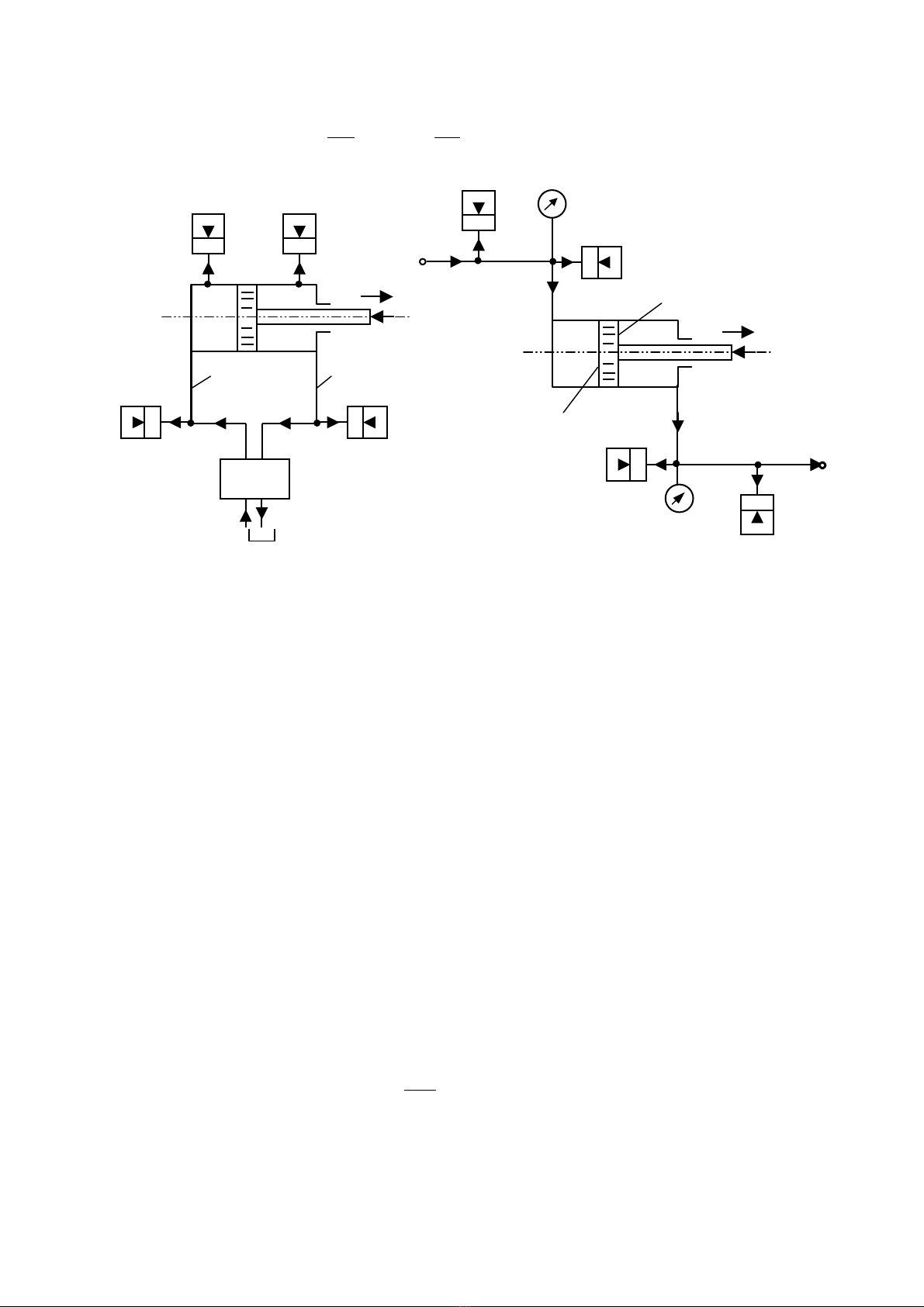
H×nh 2.3a lµ s¬ ®å côm van- xylanh thñy lùc khi c¶ hai buång A vµ B ®Òu cã ¸p suÊt
thay ®æi vµ tÝnh ®Õn ®é ®µn håi cña dÇu.
Ph−¬ng tr×nh c©n b»ng l−u l−îng cã d¹ng :
Q
T = QP + QXA + QVP (2.8)
vµ QR = QVR − QXB − QRB (2.9)
MÆt kh¸c ta thÊy r»ng :
V
A = VPA + VXA vµ VB = VRB + VXB (2.10)
nªn : B
V
CA
A= vµ B
V
CB
B= (2.11)
48
B
VRB
CR
QRB
QR
VPA
A
QT
Qp
CP
a)
van
v
FL
QR
AR
Ap
B
QvR
QxB
QRB
P
R
FL
v
CP
QP QxA
Qvp
QT
P
p
CxA
QxB
CxB
QxA
CxA
CxB
CR
b)
H×nh 2.3. M« h×nh ®iÒu khiÓn xylanh thñy lùc khi c¶ hai buång ®Òu cã dÇu ®µn håi
a- S¬ ®å chung; b - M« h×nh tÝnh to¸n.
CP vµ CR - hÖ sè tÝch lòy ®µn håi cña dÇu trªn ®−êng èng vµo vµ ra;
CXA vµ CXB - hÖ sè tÝch lòy ®µn håi cña dÇu trong c¸c buång A vµ B cña xylanh;
VPA vµ VRB - thÓ tÝch chøa dÇu trªn ®−êng èng vµo vµ ra cña xylanh;
VXA vµ VXB - thÓ tÝch chøa dÇu trong c¸c buång A vµ B cña xylanh;
QP vµ QRB - thµnh phÇn l−u l−îng dÇu bÞ nÐn trªn ®−êng èng vµo vµ ra cña xylanh;
QXA vµ QXB - thµnh phÇn l−u l−îng bÞ nÐn trong c¸c buång A vµ B cña xylanh;
QVP vµ QVR - l−u l−îng ®Èy pitt«ng chuyÓn ®éng víi vËn tèc v vµ l−u l−îng pitt«ng
®Èy dÇu ra khái xylanh;
QT vµ QR - l−u l−îng cung cÊp vµ l−u l−îng vÒ cña van.
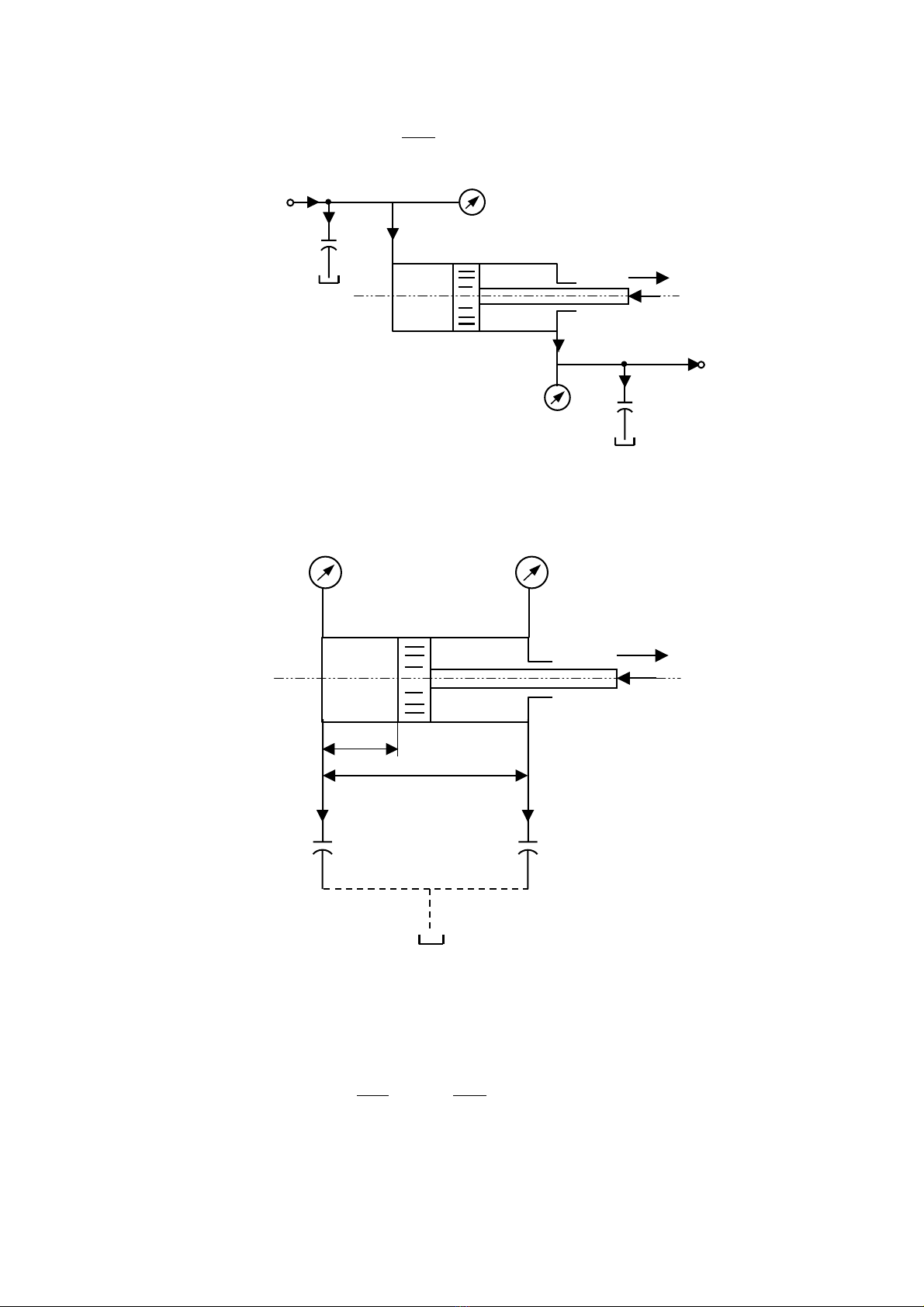
Theo c¸c c«ng thøc (2.8), (2.9), (2.10) vµ (2.11) th× h×nh 2.3 cã thÓ thay thÕ b»ng
h×nh 2.4.
Ph−¬ng tr×nh l−u l−îng lµ :
VP
P
AT Q
dt
dP
.CQ += (2.12)
vµ : VR
R
BR Q
dt
dP
.CQ += (2.13)
49
H×nh 2.4. M« h×nh tÝnh to¸n cña côm van.xylanh
P
P
QA QvP
FL
v
CA
QvR
pR
QB
C
B
QT
2.3. X¸c ®Þnh hÖ sè tÝch lòy ®µn håi cùc ®¹i cña xylanh
FL
V
CA
QA
L
x
QB
CB
P
R
P
P
H×nh 2.5. M« h×nh x¸c ®Þnh hÖ sè tÝch lòy ®µn håi cùc ®¹i cña xylanh
NÕu l−u l−îng dÇu bÞ nÐn ë c¸c buång cña xylanh b»ng nhau QA = - QB, nghÜa lµ :
dt
dP
.C
dt
dP
.C R
B
P
A−= (2.14)
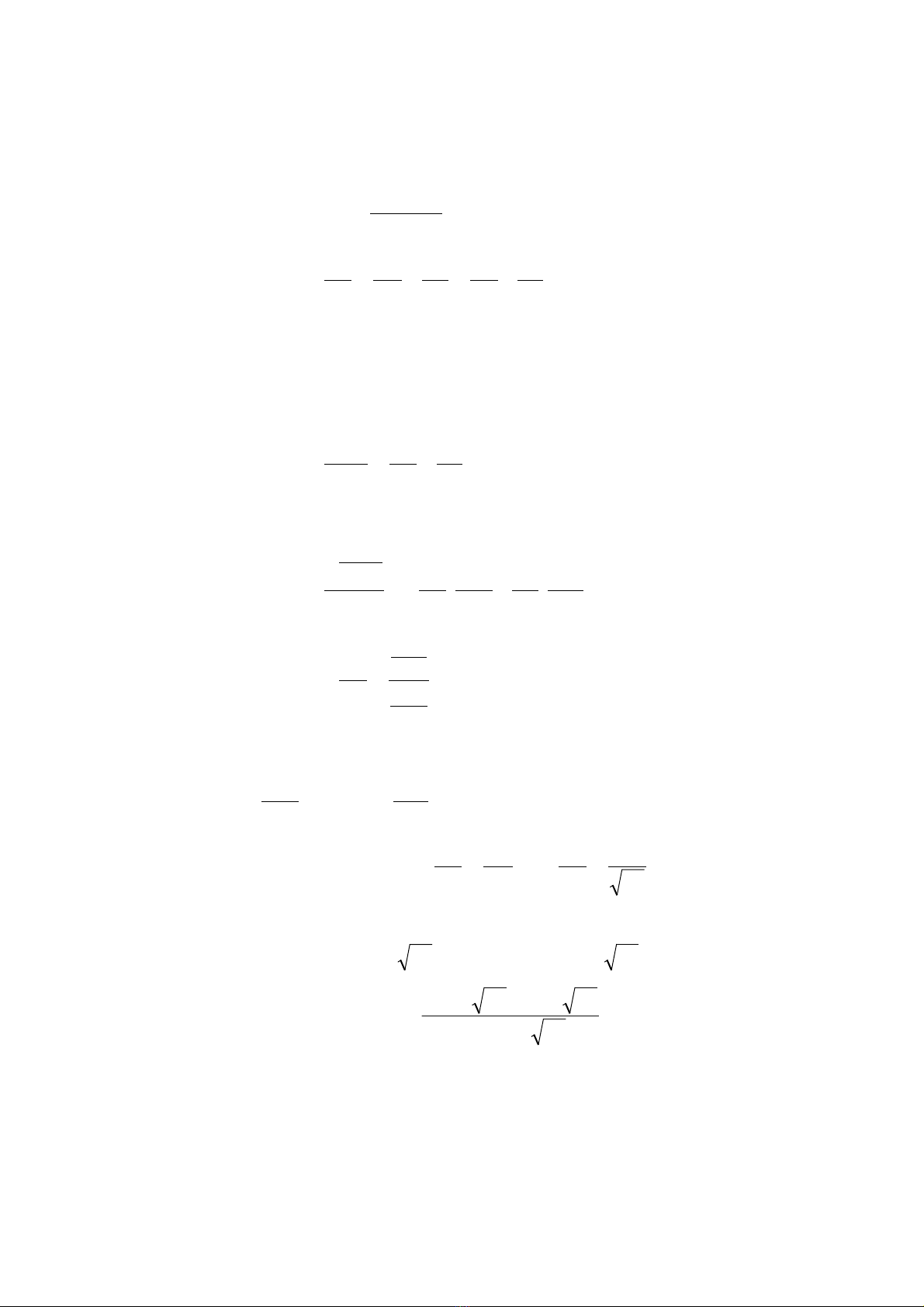
M« h×nh nµy t−¬ng ®−¬ng víi m« h×nh cã l−u l−îng b»ng nhau vµ ¸p suÊt thay ®æi
kh¸c nhau ë h×nh 2.2. Nªn còng cã thÓ tÝnh hÖ sè tÝch lòy ®µn håi t−¬ng ®−¬ng cña
h×nh 2.5 theo c«ng thøc (2.15).
BA
BA
TCC
C.C
C+
= (2.15)
hay :
BABAT V
B
V
B
C
1
C
1
C
1+=+= (2.16)
Khi nghiªn cøu ®Õn vÊn ®Ò nµy ng−êi ta ®· kh¼ng ®Þnh r»ng, nÕu hÖ sè CT cùc ®¹i th×
tÇn sè dao ®éng riªng cña xylanh sÏ cùc tiÓu.
Muèn t×m vÞ trÝ cña pitt«ng ®Ó CT cùc ®¹i ng−êi ta tÝnh to¸n nh− sau :
C«ng thøc (2.16) cã thÓ viÕt l¹i lµ :
BAT V
1
V
1
C.B
1+= (2.17)
LÊy ®¹o hµm hai vÕ cña (2.17) theo x ta cã :
0
dx
dV
.
V
1
dx
dV
.
V
1
dx
C.B
1
d
B
2
B
A
2
A
T=−−= (2.18)
Suy ra :
dx
dV
dx
dV
V
V
A
B
2
A
2
B=− (2.19)
Mµ : VA = AP.x + VPA Vµ VB = AR.(L−x) + VRB
(2.20)
nªn : P
AA
dx
dV = vµ R
BA
dx
dV −= (2.21)
Thay (2.21) vµo (2.19) ta ®−îc :
P
R
2
A
2
B
A
A
V
V= hay
x
A
B1
V
V
ρ
= (2.22)
Do ®ã c«ng thøc (2.20) ®−îc viÕt l¹i nh− sau :
(
)
xRBRxBPAP .V)xL(A.VVx.A ρ+−=ρ=+ (2.23)
Suy ra : PA
xRP
xRBxR V
.AA
.V.L.A
x−
ρ+
ρ+ρ
=
50
V×
R
P
xA
A
=ρ nªn :
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
ρ
+
−ρ
⎥
⎦
⎤
⎢
⎣
⎡+
ρ
=
x
P
PAxRB
x
.P
1
1A
V.V
LA
x (2.24)
Nh− vËy khi x x¸c ®Þnh theo c«ng thøc (2.24) th× CT sÏ ®¹t cùc ®¹i (víi 0 ≤ x ≤ L).
2.4. §é cøng thñy lùc vµ ®é cøng t−¬ng ®−¬ng
X
x1 x2 xgh
FL
P
1
2
p0
FL
V0
CH AP
X(t)
P
b)
a)
H×nh 2.6. M« h×nh nghiªn cøu ®é ®µn håi cña dÇu
a- M« h×nh thÝ nghiÖm; b- §Æc tÝnh p - x.
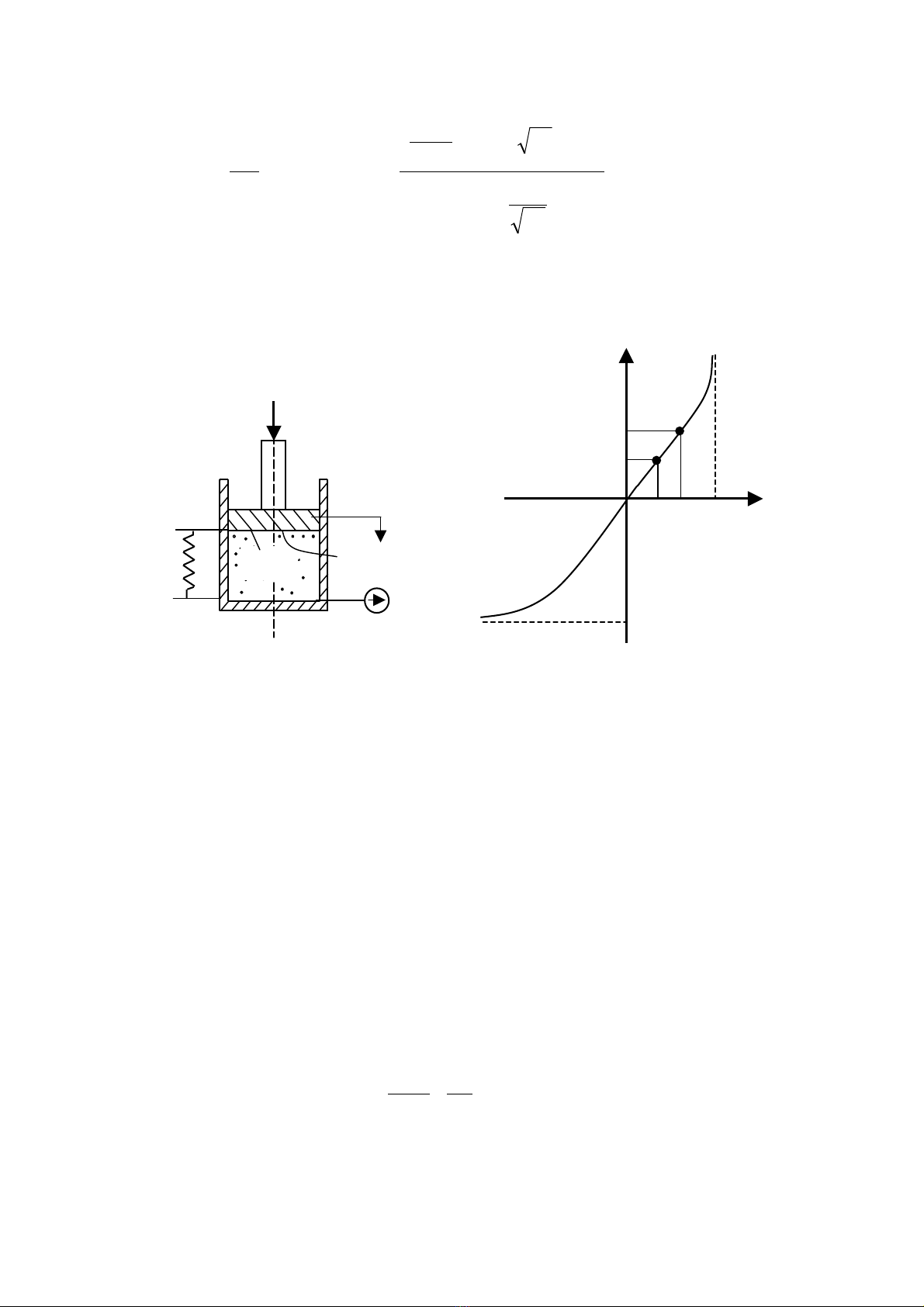
H×nh 2.6a lµ m« h×nh thÝ nghiÖm nghiªn cøu sù ®µn håi cña dÇu. NÕu thµnh xylanh,
cÇn dÉn cña pitt«ng cøng tuyÖt ®èi, kh«ng tÝnh ®Õn ma s¸t vµ sù rß dÇu th× khi t¨ng lùc
Ðp FL, ¸p suÊt P t¨ng (P t¨ng tØ lÖ víi FL) ®ång thêi ®é dÞch chuyÓn cña pitt«ng x còng
t¨ng tØ lÖ thuËn víi P. Qu¸ tr×nh ®ã thÓ hiÖn ë ®Æc tÝnh trªn h×nh 2.6b.
Trong ph¹m vi nhÊt ®Þnh, quan hÖ P - x ®−îc coi lµ tuyÕn tÝnh. §Æc tÝnh nµy gièng
®Æc tÝnh cña mét lß xo hay mét kh©u ®µn håi c¬ khÝ nµo ®ã. NghÜa lµ P t¨ng th× x t¨ng
nh−ng ®Õn mét gi¸ trÞ giíi h¹n xgh th× dï P t¨ng nh−ng x kh«ng t¨ng n÷a.
Nh− vËy trong ph¹m vi quan hÖ P - x tuyÕn tÝnh th× ®é ®µn håi cña dÇu t−¬ng ®−¬ng
®é ®µn håi cña mét lß xo vµ ®é cøng cña kh©u ®µn håi thñy lùc ®−îc gäi lµ ®é cøng
thuû lùc CH.
Theo tÝnh to¸n lý thuyÕt ë môc 3.6, nÕu tÝnh ®Õn c¶ hÖ sè ma s¸t f vµ søc c¶n thñy
lùc RL th× ®é cøng thñy lùc ®−îc x¸c ®Þnh theo c«ng thøc nh− sau :
C
A
R.C
f
C
2
P
L
H+= (2.25)
51