
S GIÁO D C VÀ ĐÀO T O THANH HÓAỞ Ụ Ạ
TR NG ƯỜ THPT BA ĐÌNH
SÁNG KI N KINH NGHI MẾ Ệ
M T S KINH NGHI M H NG D N H C SINH L P 12Ộ Ố Ệ ƯỚ Ẫ Ọ Ớ
CÁCH GI I CÁC D NG TOÁN V TÍNH TÍCH PHÂN C B NẢ Ạ Ề Ơ Ả
B C THPTỞ Ậ
Ng i th c hi n: ườ ự ệ Mai Huy Sáu
Ch c v : Giáo Viênứ ụ
SKKN thu c môn: Toán ộ
1

THANH HÓA NĂM 2016
M C L CỤ Ụ
Trang
1. M đuở ầ
- Lý do ch n đ tài..................................................................................1 ọ ề
- M c đích nghiên c u........................................................................... 2 ụ ứ
- Đi t ng nghiên c u.......................................................................... 2 ố ượ ứ
- Ph ng pháp nghiên c u..................................................................... 2 ươ ứ
2. N i dung sáng ki n.ộ ế
2.1. C s lý lu n c a sáng ki n kinh nghi m ...................................... 2 ơ ở ậ ủ ế ệ
2.2. Th c tr ng v n đ .......................................................................... 3 ự ạ ấ ề
2.3. Các sáng ki n kinh nghi m ho c các gi i pháp đã đc s d ngế ệ ặ ả ượ ử ụ
2.3.1. M t s tích phân c b n c a hàm s phân th c h u t ................ 4ộ ố ơ ả ủ ố ứ ữ ỷ
2.3.2. M t s tích phân c b n c a hàm s vô t .................................. 6ộ ố ơ ả ủ ố ỷ
2.3.3. M t s tích phân c b n c a hàm s l ng giác ......................... 12 ộ ố ơ ả ủ ố ượ
2.3.4. M t s tích phân c b n c a hàm s mũ và lôgarit..................... 15ộ ố ơ ả ủ ố
2

2.4. Hi u qu SKKN ............................................................................ 19 ệ ả
3. K t lu n, ki n ngh ............................................................................. 19ế ậ ế ị
1. M đuở ầ
- Lý do ch n đ tài.ọ ề
+ Tính tích phân là bài toán th ng g p trong các k thi t t nghi p THPT và kườ ặ ỳ ố ệ ỳ
thi tuy n sinh vào đi h c. Rèn luy n cho hể ạ ọ ệ ọc sinh có k năng tính tích phân làỹ
nhi m v đc bi t quan tr ng. Trong quá trình d y h c môn Toán nói chung vàệ ụ ặ ệ ọ ạ ọ
d y bài t p v tính tích phân trong ch ng trình trung h c ph thông h c sinhạ ậ ề ươ ọ ổ ọ
th ng lung túng không bi t h ng suy nghĩ tìm tòi l i gi i, h c sinh không bi tườ ế ướ ờ ả ọ ế
bài này thì đi bi n hay dùng ph ng pháp tích phân t ng ph n. ổ ế ươ ừ ầ
+ Đi v i nh ng bài toán nh v y, giáo viên c n h ng d n h c sinh tìm tòiố ớ ữ ư ậ ầ ướ ẫ ọ
đ phát hi n ra l i gi i, nh m trang b cho h c sinh tri th c suy lu n, t duy sángể ệ ờ ả ằ ị ọ ứ ậ ư
t o trong gi i toán. Chúng ta có th thông qua nh ng h ng d n gi i bài toánạ ả ể ữ ướ ẫ ả
“bài toán g c” có trong sách giáo khoa d n truy n th cho h c sinh suy nghĩ phátố ầ ề ụ ọ
hi n l i gi i. Xu t phát t bài toán “bài toán g c” đnh h ng cho h c sinh “suyệ ờ ả ấ ừ ố ị ướ ọ
lu n” t đó “quy bài toán l ” v “bài toán quen” c ng c lòng tin cho h c sinhậ ừ ạ ề ủ ố ọ
h c toán, say mê v i toán và gi i toán có hi u qu . D y và h ng d n h c sinhọ ớ ả ệ ả ạ ướ ẫ ọ
gi i toán tích phân c p THPT, tôi đt câu h i: “Làm th nào đ giúp h c sinhả ở ấ ặ ỏ ế ể ọ
ch đng gi i toán tích phân, h c sinh tin t ng là gi i đc bài toán tích phânủ ộ ả ọ ưở ả ượ
có trong sách giáo khoa, các bài toán tích phân trong k thi THPT Qu c gia?”.ỳ ố
+ Trong kho ng th i gian gi ng d y và nghiên c u v tích phân, tôi nh n th yả ờ ả ạ ứ ề ậ ấ
hi n ch a có các tài li u nghiên c u nào bàn sâu và chi ti t v cách gi i bài t pệ ư ệ ứ ế ề ả ậ
tích phân c b n th ng g p.ơ ả ườ ặ
+ Qua gi ng d y, tôi đúc rút kinh nghi m và mong mu n trao đi v i đngả ạ ệ ố ổ ớ ồ
nghi p m t s h ng suy nghĩ đ gi i quy t m t s bài t p tích phân c b n -ệ ộ ố ướ ể ả ế ộ ố ậ ơ ả
d ng quen thu c (không có ý tìm ra hay đa ra cách gi i t ng quát cho m t d ngạ ộ ư ả ổ ộ ạ
toán tích phân c th , hay nêu bài toán t ng quát và l i gi i t ng quát cho tíchụ ể ổ ờ ả ổ
phân y, mà tôi ch nêu các h ng giúp h c sinh “bi t đnh h ng cách gi i”ấ ỉ ướ ọ ế ị ướ ả , suy
lu n đc khi gi i toán tích phân).ậ ượ ả
- M c đích nghiên c u: ụ ứ
+ Nghiên c u đ tài nh m t ng h p các b c h ng d n h c sinh gi i bài t pứ ề ằ ổ ợ ướ ướ ẫ ọ ả ậ
tích phân c b n m t cách h p lý và đt hi u qu nhanh nh t.ơ ả ộ ợ ạ ệ ả ấ
+ Trên c s nh ng kinh nghi m c a b n thân, cùng v i nh ng trao đi v iơ ở ữ ệ ủ ả ớ ữ ổ ớ
đng nghi p đ tìm ra các gi i pháp h u hi u v n d ng trong quá trình h ngồ ệ ể ả ữ ệ ậ ụ ướ
3
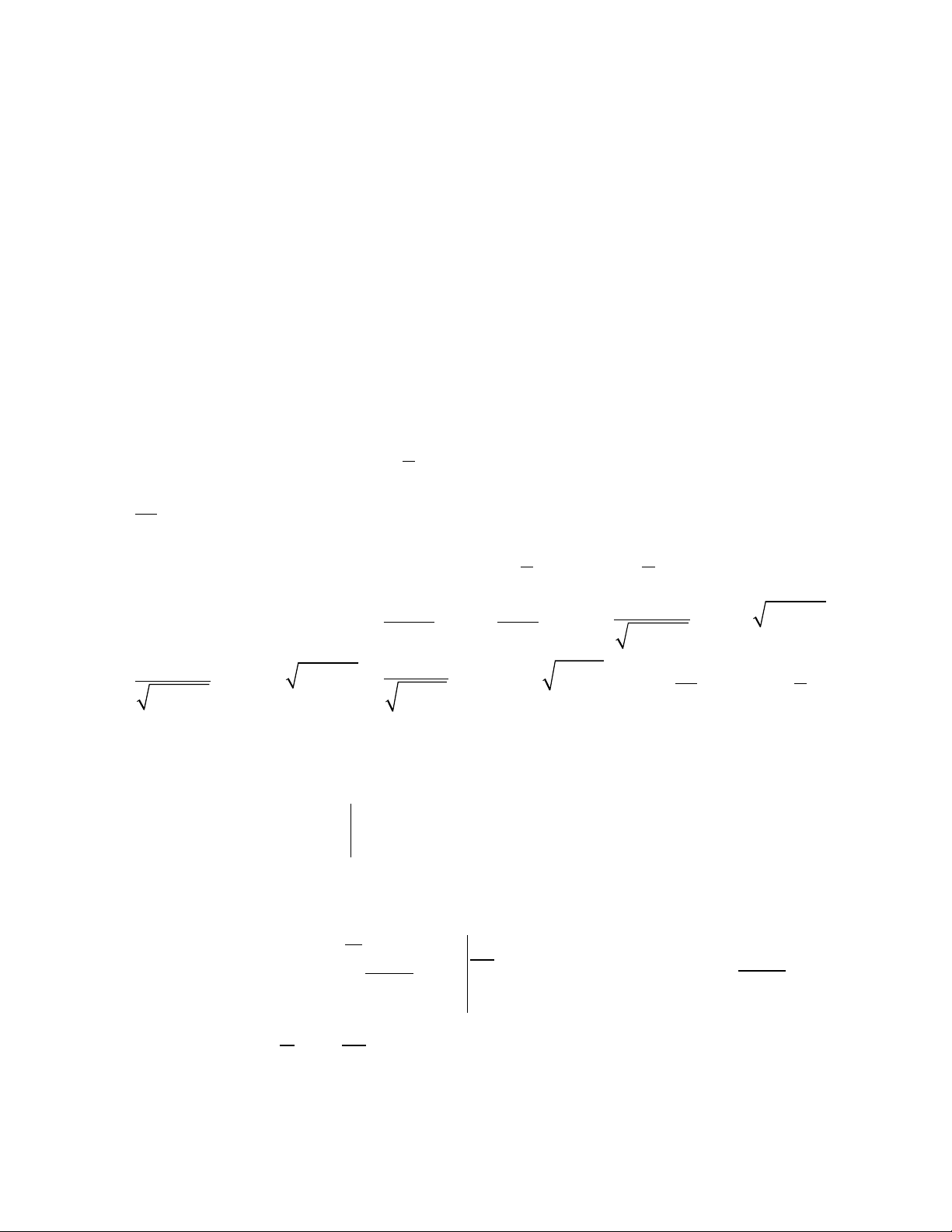
d n h c sinh gi i bài t p tích phân c b n. Góp ph n nâng cao ch t l ng d yẫ ọ ả ậ ơ ả ầ ấ ượ ạ
h c môn Toán l p 12.ọ ở ớ
- Đi t ng nghiên c u: Các bài toán tích phân c b n th ng g p trong ch ngố ượ ứ ơ ả ườ ặ ươ
trình gi i tích l p 12.ả ớ
- Ph ng pháp nghiên c u: ươ ứ
+ Xây d ng c s lí thuy t.ự ơ ở ế
+ Kh o sát th c t .ả ự ế
+ Ph ng pháp phân tích, suy lu n, t ng h p, so sánh…ươ ậ ổ ợ
2. N i dung sáng ki n kinh nghi mộ ế ệ
2.1. C s lý lu n c a sáng ki n kinh nghi mơ ở ậ ủ ế ệ
1) B ng các nguyên hàm c b n, các tính ch t c a nguyên hàm, các tính ch t c aả ơ ả ấ ủ ấ ủ
tích phân (SGK gi i tích l p 12)ả ớ
2) Đ gi i toán tích phân h c sinh ph i n m đc các vi phân “c b n” th ng ể ả ọ ả ắ ượ ơ ả ườ
g p, Ch ng h n:ặ ẳ ạ
1
( ) ( )dx d x b d ax b
a
= + = +
v i ớ
0a
;
( ) ( )
x x x
d e d e c e dx= + =
;
(ln )
dx d x
x=
;
sin (cos ) (cos )xdx d x d x b=− =− +
;
1 1
sin (cos ) (cos )kxdx d kx d kx b
k k
=− =− +
, v i ớ
0k
Các vi phân ph c t p h n: ứ ạ ơ
2
sin 1
( )
cos
cos
xdx d x
x
=
;
2 2
2 2
( )
xdx d x a
x a
= +
+
2 2
2 2
( )
xdx d a x
a x
= − −
−
;
2
2
ln( )
dx d x x k
x k
� �
= + +
� �
� �
+
;
2
1 1
(1 ) ( )dx d x x
x
− = +
...
3) Ngoài ra h c sinh ph i n m đc các v n đ c t y u sau đây: ọ ả ắ ượ ấ ề ố ế
a) S d ng thành th o đnh lý Niu t n – Leibnitz(SGK GT 12): ử ụ ạ ị ơ
N u hàm s ế ố
( )y f x=
liên t c trên ụ
[ ]
;a b
và
( )
F x
là m t nguyên hàm c a hàm sộ ủ ố
( )
f x
thì
( ) ( ) ( )
( )
b
a
b
f x dx F x F b F a
a
= = −
Chú ý: Gi thi t ả ế
( )
f x
liên t c trên ụ
[ ]
;a b
là đi u ki n b t bu c ph i có đ đcề ệ ắ ộ ả ể ượ
s d ng đnh lý. M t s h c sinh c t ng có đc ử ụ ị ộ ố ọ ứ ưở ượ
( )
F x
là tính đc tích phân, ượ
ch ng h n n u vi t ẳ ạ ế ế
( )
3
4
2
0
3
1 ?
4
0
dx
I tanx
cos x
ππ
= = =
Ta đã bi t ế
( )
2
1
os
f x c x
=
không
xác đnh t i x = ị ạ
3
0;
2 4
π π
� �
� �
� �
nên
I
không t n t i. ồ ạ
b) Ph ng pháp đi bi n s . ươ ổ ế ố
4
C s c a nó là đnh lý sau: N u t =ơ ở ủ ị ế
( )x
ϕ
đn đi u trên đo n ơ ệ ạ
[ ]
;a b
thì
( )
,
( )
( ( )) ( ) ( )
b
b
a a
f x x dx f t dt
ϕ
ϕ
ϕ ϕ
=
� �
. (SGK gi i tích l p 12)ả ớ
c) Ph ng pháp tích phân t ng ph n.ươ ừ ầ
Ta có:
b b
a a
b
udv uv vdu
a
= −
� �
. (SGK gi i tích l p 12)ả ớ
2.2 Th c tr ng v n đ tr c khi áp d ng sáng ki n kinh nghi m:ự ạ ấ ề ướ ụ ế ệ
Qua gi ng d y bài toán tính tích phân, h c sinh th ng lúng túng g p nhi uả ạ ọ ườ ặ ề
khó khăn. Không bi t bài này dùng ph ng pháp tính nào đi bi n hay tích phânế ươ ổ ế
t ng ph n), n u đi bi n s thì đi nh th nào(đt ừ ầ ế ổ ế ố ổ ư ế ặ
x=
t
hay
( )
t u x=
), còn
n u dùng ph ng pháp tích phân t ng ph n thì không bi t ch n ế ươ ừ ầ ế ọ
u
và
dv
sao cho
thích h p…K t qu kh o sát khi tôi d y ph n tích phân cho h c sinh l p 12 nămợ ế ả ả ạ ầ ọ ớ
h c 2013- 2014 khi ch a áp d ng sáng ki n này:ọ ư ụ ế
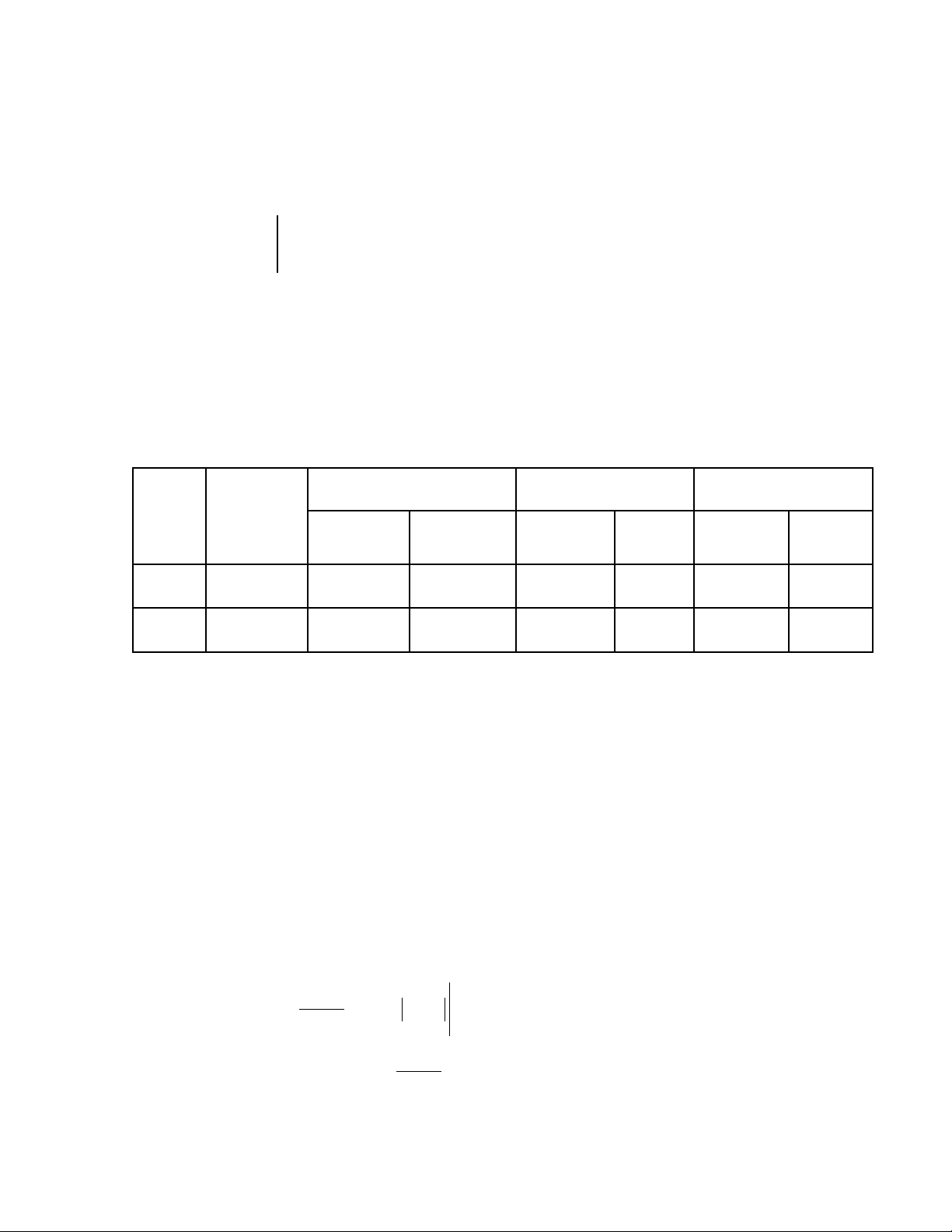
L pớSĩ sốĐi m < 5ểĐi m 5ể
< 8 Đi m ể
8
s l ngố ượ %số
l ngượ %số
l ngượ %
12D 38 13 34,21 23 60,52 2 5,27
12P 47 17 36,17 24 51,06 6 12,77
T k t qu trên tôi nh n th y t l h c sinh có s đi m d i trung bình là quáừ ế ả ậ ấ ỉ ệ ọ ố ể ướ
cao, trong khi đó h c sinh đt đi m gi i l i quá th p. Đi u này khi n b n thânọ ạ ể ỏ ạ ấ ề ế ả
tôi ph i trăn tr tìm ra ph ng pháp h ng d n h c sinh bi t cách gi i các d ngả ở ươ ướ ẫ ọ ế ả ạ
toán tích phân c b n m t cách d dàng và hi u qu nh t. ơ ả ộ ễ ệ ả ấ
2.3 Các gi i pháp đc s d ng trong vi c h ng d n h c sinh gi i cácả ượ ử ụ ệ ướ ẫ ọ ả
tích phân c b n.ơ ả
Thông qua m t s d ng tích phân c b n tôi h ng d n cho h c sinh các cáchộ ố ạ ơ ả ướ ẫ ọ
ti p c n khác nhau, áp d ng vào gi i các tích phân đn gi n khác:ế ậ ụ ả ơ ả
Các tích phân “c b n” và các cách tính ph bi nơ ả ổ ế (v i gi thi t hàm s d i ớ ả ế ố ướ
d u tích phân liên t c trong đo n đang xét): ấ ụ ạ
2.3.1. M t s tích phân c b n c a hàm s phân th c h u t :ộ ố ơ ả ủ ố ứ ữ ỷ
a) Tích phân
'
1
( ) ln ( )
( )
f x
I dx f x
f x
β
α
β
α
= =
Ví d 1:ụ Tinh tích phân
I=
3
1
2
01
xdx
x+
5


























