143
Hμm nμy cã nghiÖm d−¬ng duy nhÊt z = 22
βα
+ mμ nã cho phÐp t×m a1 trong
hμm träng l−îng.
§Ó x¸c ®Þnh c¸c hÖ sè A1 vμ A ta sö dông hÖ (5.6.22) d−íi d¹ng
=+
+−+
=+
−−+
+−
−−
Ti
Ti
eA
i
A
eA
i
A
)(
22
1
)(
22
1
)(
,
)(
βα
βα
βαβα
βαβα
(5.6.38)
Gi¶i hÖ nμy ta ®−îc
(
)
TeA T
β
β
βααβα
α
sin
22222
1
−
+−+
= (5.6.39)
−+
+= −TTeA T
β
β
αβα
β
α
sincos
22
(5.6.40)
Cuèi cïng hμm träng l−îng cã d¹ng
g(t) =
()
+
−−+ +− T
Te 22
sin
22222
βα
β
β
βαβαα
+ T
etTT
α
δβ
β
αβα
β
−
−+
+)(sincos
22
(5.6.41)
KÕt qu¶ nhËn ®−îc nμy chÝnh lμ kÕt qu¶ trong vÝ dô 2 môc 5.5.
Ch−¬ng 6: X¸c ®Þnh c¸c ®Æc tr−ng cña hμm ngÉu nhiªn theo sè
liÖu thùc nghiÖm
6.1. C¸c ®Æc tr−ng thèng kª cña hμm ngÉu nhiªn
ë ch−¬ng 2 chóng ta ®· thÊy r»ng, trong lý thuyÕt t−¬ng quan, ng−êi ta lÊy kú väng
to¸n häc vμ hμm t−¬ng quan lμm ®Æc tr−ng cña hμm ngÉu nhiªn. Ta xÐt ph−¬ng ph¸p
x¸c ®Þnh c¸c ®Æc tr−ng nμy theo sè liÖu thùc nghiÖm. Trong ®ã cÇn nhí r»ng, khi sö dông
c¸c sè liÖu thùc nghiÖm ta kh«ng bao giê gi¶ thiÕt cã tËp hîp tÊt c¶ c¸c thÓ hiÖn cã thÓ
cña hμm ngÉu nhiªn, mμ chØ cã mét sè h÷u h¹n c¸c thÓ hiÖn, lμ mét phÇn nμo ®ã trong
tËp tæng thÓ.
V× vËy, c¸c ®Æc tr−ng cña hμm ngÉu nhiªn ®−îc x¸c ®Þnh theo tËp mÉu nμy mang
tÝnh chÊt ngÉu nhiªn vμ cã thÓ kh¸c víi nh÷ng ®Æc tr−ng thùc x¸c ®Þnh theo toμn bé tËp
tæng thÓ c¸c thÓ hiÖn. Nh÷ng ®Æc tr−ng nhËn ®−îc theo sè liÖu thùc nghiÖm gäi lμ nh÷ng
®Æc tr−ng thèng kª hay −íc l−îng thèng kª. Kh¸c víi gi¸ trÞ thùc cña kú väng to¸n häc
144
)(tm vμ hμm t−¬ng quan ),( 21 ttR , ta sÏ ký hiÖu c¸c ®Æc tr−ng thèng kª t−¬ng øng d−íi
d¹ng ),(
~
),(
~
21 ttRtm .
Cã thÓ xÐt hμm ngÉu nhiªn nh− tËp hîp tÊt c¶ c¸c l¸t c¾t cña nã. XuÊt ph¸t tõ ®ã,
cã thÓ ®−a viÖc x¸c ®Þnh c¸c ®Æc tr−ng thèng kª cña hμm ngÉu nhiªn vÒ viÖc x¸c ®Þnh c¸c
®Æc tr−ng t−¬ng øng cña hÖ c¸c ®¹i l−îng ngÉu nhiªn.
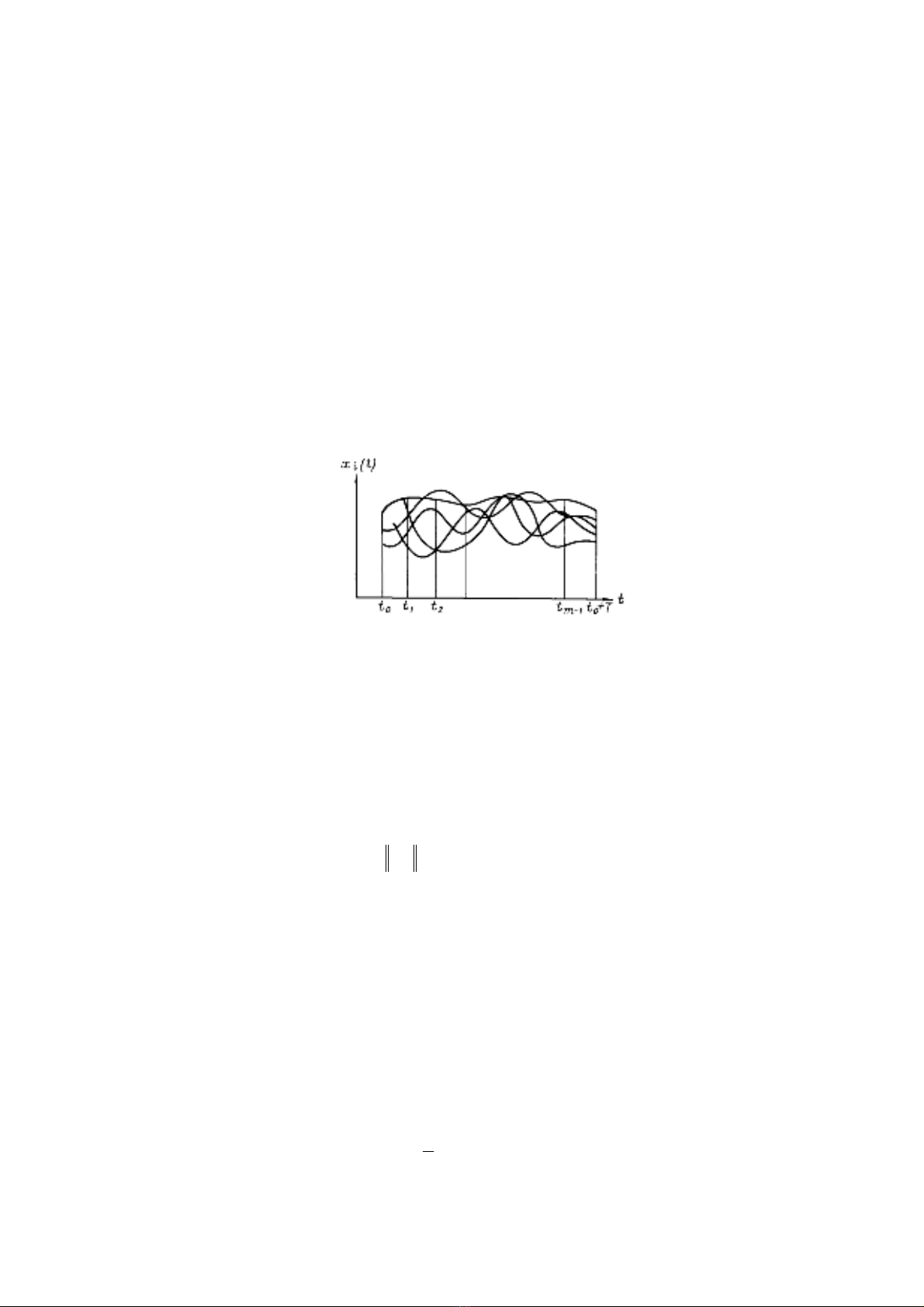
Gi¶ sö do kÕt qu¶ thùc nghiÖm ta nhËn ®−îc n thÓ hiÖn ),,()( nitX i ..., 2 1 = cña qu¸
tr×nh ngÉu nhiªn )(tX trªn kho¶ng Tttt +≤≤ 00 (h×nh 6.1).
Ta sÏ chia kho¶ng nμy thμnh m phÇn b»ng nhau bëi c¸c ®iÓm Ttttt m+
−0110 ..., ,,, . §èi
víi mçi gi¸ trÞ cña ®èi sè j
t ),,( mj ..., 2 1= ta nhËn ®−îc mét l¸t c¾t cña qu¸ tr×nh ngÉu
nhiªn )( jj tXX = lμ mét ®¹i l−îng ngÉu nhiªn, tøc lμ ta nhËn ®−îc hÖ m ®¹i l−îng ngÉu
nhiªn. Vμ thay cho c¸c ®Æc tr−ng thèng kª cña qu¸ tr×nh ngÉu nhiªn ta sÏ xÐt nh÷ng ®Æc
tr−ng t−¬ng øng cña hÖ c¸c ®¹i l−îng ngÉu nhiªn nμy.
H×nh 6.1
Theo môc 1.8, nh÷ng ®Æc tr−ng ®ã lμ: kú väng to¸n häc cña c¸c ®¹i l−îng ngÉu
nhiªn
[
]
)(
~
~
jxj tmXm = (6.1.1)
lμ nh÷ng gi¸ trÞ thèng kª cña kú väng to¸n häc cña qu¸ tr×nh ngÉu nhiªn t¹i c¸c gi¸ trÞ
rêi r¹c cña ®èi sè tj, vμ ma trËn t−¬ng quan
=
mm
m
m
lj
R
RR
RRR
R
~
......
~
...
~
~
...
~~
~
,
222
11211
. (6.1.2)
C¸c phÇn tö cña ma trËn t−¬ng quan (6.1.2) lμ m«men t−¬ng quan thèng kª gi÷a c¸c
l¸t c¾t cña qu¸ tr×nh ngÉu nhiªn, øng víi c¸c gi¸ trÞ cña ®èi sè j
t vμ l
t, tøc lμ c¸c gi¸ trÞ
thèng kª cña hμm t−¬ng quan cña qu¸ tr×nh ngÉu nhiªn t¹i nh÷ng gi¸ trÞ rêi r¹c cña ®èi sè
j
t vμ l
t
),(
~
~
,ljxlj ttRR =.
Theo luËn ®iÓm cña thèng kª to¸n häc (ch¼ng h¹n, xem [8]), ng−êi ta xem trung
b×nh sè häc cña n gi¸ trÞ hiÖn cã cña ®¹i l−îng ngÉu nhiªn lμ gi¸ trÞ thèng kª cña kú väng
to¸n häc
mjtx
n
tm j
n
i
ijx ..., 2 1
1
1
,,),()(
~==
=
. (6.1.3)
145
T−¬ng tù, c¸c gi¸ trÞ thèng kª cña m«men t−¬ng quan ®−îc x¸c ®Þnh theo c«ng thøc
[]
[]
)(
~
)()(
~
)(),(
~
lxli
n
i
jxjiljx tmtxtmtx
n
ttR −−
−
=
=
1
1
1
(6.1.4)
§Æc biÖt, khi lj = m«men t−¬ng quan lμ gi¸ trÞ thèng kª cña ph−¬ng sai t¹i l¸t c¾t
t−¬ng øng
[]
=
−
−
==
n
i
jxjijjxjx tmtx
n
ttRtD
1
2
1
1)(
~
)(),(
~
)(
~. (6.1.5)
C¸c gi¸ trÞ thèng kª cña hÖ sè t−¬ng quan ),(
~
~
,ljxlj ttrr = lμ nh÷ng gi¸ trÞ thèng kª
cña hμm t−¬ng quan chuÈn ho¸ ),(
~
ljx ttr t¹i nh÷ng gi¸ trÞ ®èi sè j
t, l
t, ®−îc x¸c ®Þnh theo
c«ng thøc
)(
~
)(
~
),(
~
),(
~
lxjx
ljx
ljx tt
ttR
ttr σσ
=
, (6.1.6)
trong ®ã )(
~
)(
~tDt xx =σ .
Ph−¬ng ph¸p võa xÐt trªn ®©y, lÊy trÞ sè trung b×nh sè häc theo tÊt c¶ c¸c thÓ hiÖn
cã ®−îc lμm gi¸ trÞ thèng kª cña kú väng to¸n häc cña ®¹i l−îng ngÉu nhiªn, dùa trªn c¬
së sö dông quy luËt sè lín. Quy luËt nμy ph¸t biÓu r»ng, khi sè l−îng c¸c thÝ nghiÖm lμ
lín, víi x¸c suÊt gÇn b»ng ®¬n vÞ, cã thÓ cho r»ng ®é lÖch cña gi¸ trÞ trung b×nh so víi kú
väng to¸n häc lμ nhá. ë ®©y gi¶ thiÕt r»ng, c¸c thÝ nghiÖm lμ ®éc lËp vμ ®−îc tiÕn hμnh
trong nh÷ng ®iÒu kiÖn nh− nhau. C¸c thÝ nghiÖm ®−îc coi lμ tiÕn hμnh trong nh÷ng ®iÒu
kiÖn nh− nhau nÕu khi thùc hiÖn chóng, tËp hîp tÊt c¶ nh÷ng t¸c ®éng ®−îc tÝnh tíi,
®iÒu kiÖn ban ®Çu vμ nh÷ng mèi liªn hÖ ®−îc gi÷ nguyªn kh«ng ®æi. C¸c thÝ nghiÖm ®−îc
coi lμ ®éc lËp nÕu kÕt qu¶ cña mçi thÝ nghiÖm kh«ng phô thuéc vμo kÕt qu¶ cña nh÷ng
lÇn thÝ nghiÖm kh¸c. D−íi gãc ®é to¸n häc, tÝnh ®éc lËp cña c¸c lÇn thÝ nghiÖm kh¸c nhau
t−¬ng ®−¬ng víi sù ®éc lËp cña luËt ph©n bè cña hμm ngÉu nhiªn trong c¸c thÝ nghiÖm
®ã, cßn sù tån t¹i nh÷ng ®iÒu kiÖn bªn ngoμi gièng nhau khi tiÕn hμnh thÝ nghiÖm t−¬ng
®−¬ng víi viÖc c¸c quy luËt ph©n bè cña hμm ngÉu nhiªn nh− nhau trong tÊt c¶ c¸c lÇn
thÝ nghiÖm.
HÖ ph−¬ng ph¸p võa xÐt còng ®−îc øng dông ®Ó x¸c ®Þnh c¸c ®Æc tr−ng thèng kª
cña tr−êng ngÉu nhiªn.
Gi¶ sö cã n thÓ hiÖn ) ..., 2, ,1( )( niui=
ρ
cña tr−êng ngÉu nhiªn )(
ρ
U trong miÒn
kh«ng gian D nμo ®ã. Ta chia miÒn D thμnh m phÇn bëi mét tËp hîp c¸c mÆt ph¼ng
song song víi c¸c mÆt ph¼ng to¹ ®é vμ ph©n bè c¸ch ®Òu nhau. Ký hiÖu j
ρ
lμ b¸n kÝnh
vect¬ cña ®iÓm j
N, ®Ønh cña c¸c khèi lËp ph−¬ng mμ miÒn D ®· ®−îc chia thμnh. Khi ®ã
øng víi mçi gi¸ trÞ cña ®èi sè j
ρ
lμ mét ®¹i l−îng ngÉu nhiªn )( j
U
ρ
− l¸t c¾t cña tr−êng
ngÉu nhiªn t¹i ®iÓm j
N. TÊt c¶ c¸c c«ng thøc ®Ó x¸c ®Þnh c¸c ®Æc tr−ng thèng kª cña
tr−êng ngÉu nhiªn )(
ρ
U ®−îc nhËn tõ c¸c c«ng thøc t−¬ng øng cña qu¸ tr×nh ngÉu nhiªn
)(tX (6.1.3)−(6.1.6) b»ng c¸ch thay thÕ chØ sè
x
thμnh chØ sè u, cßn ®èi sè v« h−íng t ®−îc
thay b»ng ®èi sè vect¬
ρ
. Ph−¬ng ph¸p xö lý theo tËp hîp c¸c thÓ hiÖn cña hμm ngÉu
nhiªn võa xÐt ®ßi hái sè l−îng lín c¸c thÓ hiÖn, v×, nh− ®· biÕt tõ thèng kª to¸n häc, ®é
chÝnh x¸c cña c¸c ®Æc tr−ng thèng kª nhËn ®−îc gi¶m nhanh khi gi¶m sè l−îng thÓ hiÖn.
Víi sè l−îng thÓ hiÖn lín, viÖc tÝnh to¸n theo c«ng thøc (6.1.3) vμ ®Æc biÖt theo c«ng
146
thøc (6.1.4) rÊt khã kh¨n. C«ng viÖc nμy cã thÓ ®−îc thùc hiÖn mét c¸ch hiÖu qu¶ nhê
m¸y tÝnh ®iÖn tö. Ngμy nay ng−êi ta ®· lËp c¸c ch−¬ng tr×nh x¸c ®Þnh kú väng to¸n häc
vμ ma trËn t−¬ng quan cho nhiÒu lo¹i m¸y tÝnh kh¸c nhau, nhê ®ã viÖc xö lý c¸c th«ng
tin khÝ t−îng thñy v¨n ®−îc thùc hiÖn.
Th«ng th−êng trong thùc tÕ viÖc ®o ®¹c c¸c yÕu tè khÝ t−îng thñy v¨n ®−îc tiÕn
hμnh kh«ng liªn tôc ®èi víi tÊt c¶ c¸c gi¸ trÞ cña ®èi sè, mμ chØ t¹i nh÷ng gi¸ trÞ rêi r¹c
cña nã. Nh− vËy, khi x¸c ®Þnh c¸c ®Æc tr−ng cña hμm ngÉu nhiªn theo sè liÖu thùc
nghiÖm quan tr¾c khÝ t−îng thñy v¨n, chóng ta cã mét hÖ c¸c l¸t c¾t ®èi víi nh÷ng gi¸ trÞ
cô thÓ ®· cho cña ®èi sè, vμ chóng ta chØ cã thÓ thao t¸c víi hÖ ®ã.
Trong tr−êng hîp qu¸ tr×nh ngÉu nhiªn dõng hay tr−êng ®ång nhÊt ®¼ng h−íng, kú
väng to¸n häc kh«ng phô thuéc vμo ®èi sè cña hμm ngÉu nhiªn, cßn hμm t−¬ng quan lμ
hμm chØ cña mét ®èi sè v« h−íng − modul cña hiÖu c¸c ®èi sè. Khi ®ã viÖc tÝnh to¸n ®¬n
gi¶n h¬n nhiÒu, thay v× ma trËn t−¬ng quan (6.1.2) chØ cÇn tÝnh nh÷ng phÇn tö ë hμng
®Çu tiªn cña nã, ®ã chÝnh lμ c¸c m«men t−¬ng quan gi÷a c¸c l¸t c¾t n»m c¸ch nhau
nh÷ng kho¶ng kh¸c nhau cña hμm ngÉu nhiªn.
6.2. C¸c ®Æc tr−ng thèng kª cña c¸c hμm ngÉu nhiªn cã tÝnh Ego®ic
§èi víi qu¸ tr×nh ngÉu nhiªn dõng hay tr−êng ®ång nhÊt ®¼ng h−íng cã tÝnh ego®ic
viÖc lÊy trung b×nh theo tËp c¸c thÓ hiÖn (xem ch−¬ng 2) cã thÓ thay b»ng lÊy trung b×nh
theo mét thÓ hiÖn cho trªn kho¶ng biÕn thiªn ®ñ lín cña ®èi sè.
Ta xÐt c¸c ph−¬ng ph¸p x¸c ®Þnh c¸c ®Æc tr−ng thèng kª cña hμm ngÉu nhiªn trong
tr−êng hîp nμy.
Gi¶ sö cã thÓ hiÖn )(tx cña qu¸ tr×nh ngÉu nhiªn dõng ego®ic )(tX cho trªn kho¶ng
],[ T 0 .
Nh− ®· tr×nh bμy trong môc 2.6, c¸c gi¸ trÞ cña kú väng to¸n häc vμ hμm t−¬ng
quan cña qu¸ tr×nh ngÉu nhiªn ®−îc x¸c ®Þnh theo c¸c c«ng thøc (2.6.1) vμ (2.6.2).
Trong c«ng thøc (2.6.2) cã mÆt gi¸ trÞ thùc cña kú väng to¸n häc x
m cña qu¸ tr×nh
ngÉu nhiªn. Song trong ®a sè tr−êng hîp gi¸ trÞ nμy ch−a ®−îc biÕt, vμ do ®ã thay cho gi¸
trÞ thùc buéc ph¶i sö dông gi¸ trÞ thèng kª cña kú väng to¸n häc x
m
~
.
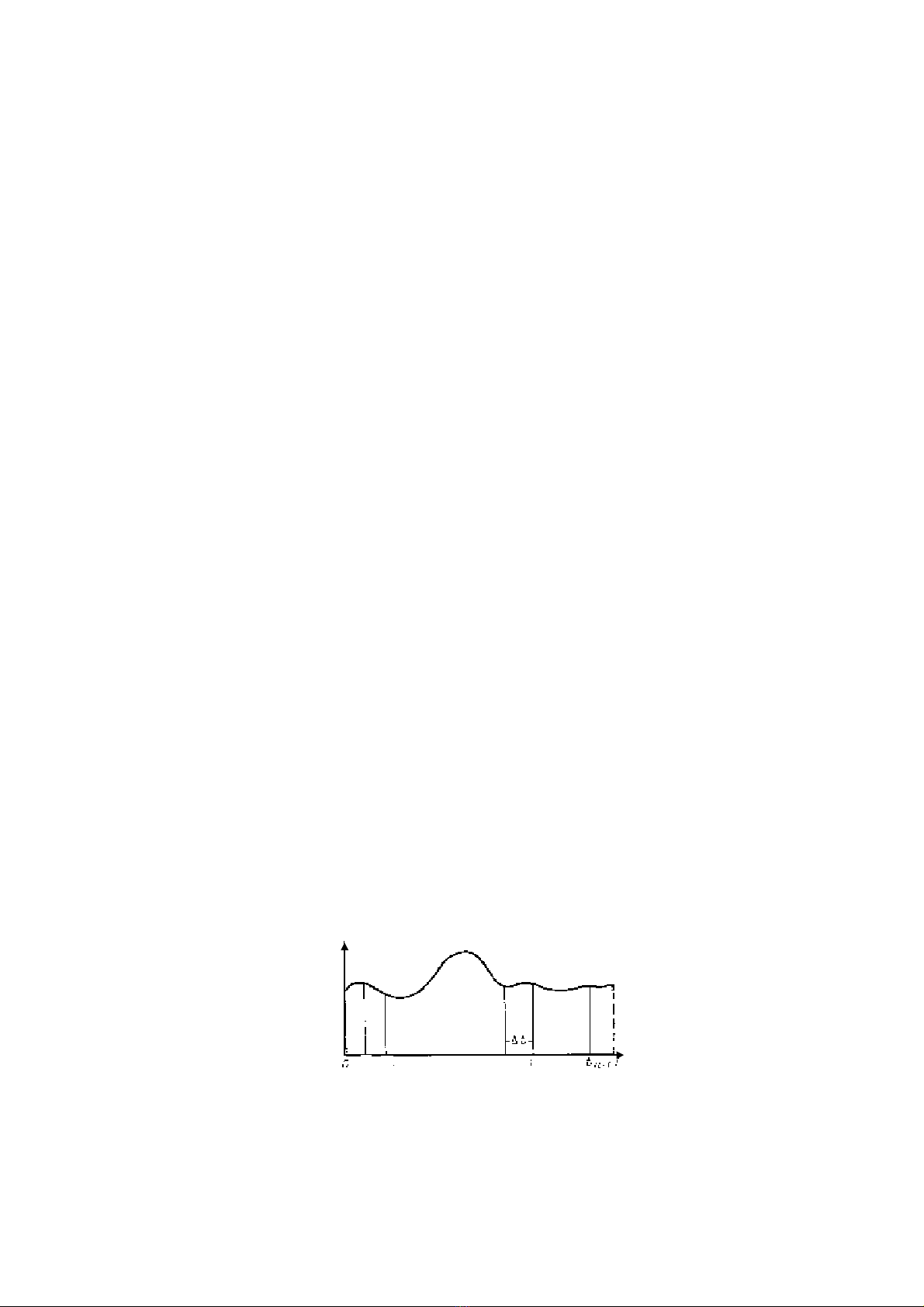
Trªn thùc tÕ chóng ta th−êng kh«ng cã biÓu thøc gi¶i tÝch cña thÓ hiÖn )(tx , mμ chØ
lμ biÓu diÔn ®å thÞ cña nã, nhËn ®−îc b»ng c¸c dông cô tù ghi, hoÆc th«ng th−êng nhÊt lμ
b¶ng c¸c gi¸ trÞ cña nã t¹i nh÷ng trÞ sè rêi r¹c cña ®èi sè t.
v
t
1
t
2
t
j-1
t
j
H×nh 6.2
Khi ®ã, trong c¸c c«ng thøc (2.6.1) vμ (2.6.2) c¸c tÝch ph©n ®−îc thay thÕ gÇn ®óng
b»ng c¸c tæng tÝch ph©n.
147
Gi¶ sö cã b¨ng ghi liªn tôc cña thÓ hiÖn )(tx (h×nh 6.2), ta chia kho¶ng ],[ T 0 thμnh
n phÇn b»ng nhau ®é dμi tΔ vμ ký hiÖu ®iÓm cuèi cña tõng ®o¹n lμ ),,( njtjt j ..., 2 1 =Δ= .
V× tnT Δ= , nªn c¸c c«ng thøc (2.6.1) vμ (2.6.2) cã thÓ viÕt d−íi d¹ng
=
Δ=
n
j
xtjx
n
m
1
1)(
~, (6.2.1)
[][ ]
x
kn
j
xkx mtkjxmtjx
kn
R~
])[(
~
)()(
~−Δ+−Δ
−
=τ
−
=
1
1
, (6.2.2)
trong ®ã ),,( mktk
k ..., 2 1 =Δ=τ .
NÕu b¨ng ghi thÓ hiÖn kh«ng liªn tôc mμ lμ rêi r¹c, th× j
t lÊy b»ng nh÷ng gi¸ trÞ
cña ®èi sè t¹i ®ã ghi gi¸ trÞ cña thÓ hiÖn )(tx .
ViÖc x¸c ®Þnh gi¸ trÞ thèng kª cña kú väng to¸n häc u
m
~
vμ hμm t−¬ng quan )(
~lRu
cña tr−êng ®ång nhÊt ®¼ng h−íng )(
ρ
U theo mét thÓ hiÖn cho trong miÒn kh«ng gian
D
còng ®−îc tiÕn hμnh b»ng c¸ch t−¬ng tù.
HÖ ph−¬ng ph¸p võa xÐt còng hoμn toμn ®−îc ¸p dông ®Ó x¸c ®Þnh hμm cÊu tróc
cña qu¸ tr×nh dõng ego®ic hay tr−êng ngÉu nhiªn ®ång nhÊt ®¼ng h−íng. C«ng thøc ®Ó
x¸c ®Þnh gi¸ trÞ thèng kª cña hμm cÊu tróc theo mét thÓ hiÖn cña hμm ngÉu nhiªn )(tX
cho trªn ®o¹n ],[ T 0 cã d¹ng
[]
τ−
−τ+
τ−
=τ
T
xdttxtx
T
B
0
2
1)()()( . (6.2.3)
Khi thay thÕ tÝch ph©n trong (6.2.3) b»ng tæng tÝch ph©n, gièng nh− ®èi víi hμm
t−¬ng quan, ta cã c«ng thøc
[]
−
=
−τ+
−
=τ
kn
j
jkjkx txtx
kn
B
1
2
1)()()(
~. (6.2.4)
NÕu kh«ng chØ cã mét thÓ hiÖn, mμ lμ mét sè c¸c thÓ hiÖn cña nã nhËn ®−îc trong
nh÷ng ®iÒu kiÖn nh− nhau, th× viÖc xö lý ®−îc tiÕn hμnh theo ph−¬ng ph¸p trªn ®èi víi
tõng thÓ hiÖn, sau ®ã lÊy trung b×nh c¸c ®Æc tr−ng tÝnh ®−îc. Trong tr−êng hîp nμy cÇn
nhí r»ng gi¸ trÞ trung b×nh cña hμm cÊu tróc nhËn ®−îc b»ng c¸ch lÊy trung b×nh theo
mét bé n thÓ hiÖn ®é dμi h÷u h¹n
T
, sÏ tiÕn tíi gi¸ trÞ thùc khi lÊy giíi h¹n ∞→n.
Cßn ®èi víi hμm t−¬ng quan, do khi tÝnh nã kh«ng sö dông gi¸ trÞ thùc mμ dïng
gi¸ trÞ thèng kª cña kú väng to¸n häc cña hμm ngÉu nhiªn, nªn gi¸ trÞ trung b×nh cña
nã, thËm chÝ c¶ khi ∞→n, vÉn bÞ sai lÖch.
Thùc vËy, ®èi víi hμm cÊu tróc ta cã
[]
[]
=
−τ+
τ−
=τ τ−
dttXtX
T
MBM
T
x
0
2
1)()()(
~
[]
{}
dttXtXM
T
Tτ−
−τ+
τ−
=
0
2
1)()( )()( τ=τ
τ−
=τ−
x
T
xBdtB
T0
1, (6.2.5)
tøc lμ kú väng to¸n häc cña hμm cÊu tróc thèng kª b»ng gi¸ trÞ thùc cña nã.
NÕu c¸c gi¸ trÞ thèng kª cña hμm t−¬ng quan ®−îc x¸c ®Þnh theo tõng thÓ hiÖn ®é
dμi
T
cã sö dông gi¸ trÞ thèng kª cña kú väng to¸n häc cña hμm ngÉu nhiªn, th×