206
H×nh 10.2
Theo c«ng thøc (10.2.9), ë ®©y cã thÓ biÓu diÔn d−íi d¹ng
ττ=
t
uu dRtD
0
)()( . (10.2.16)
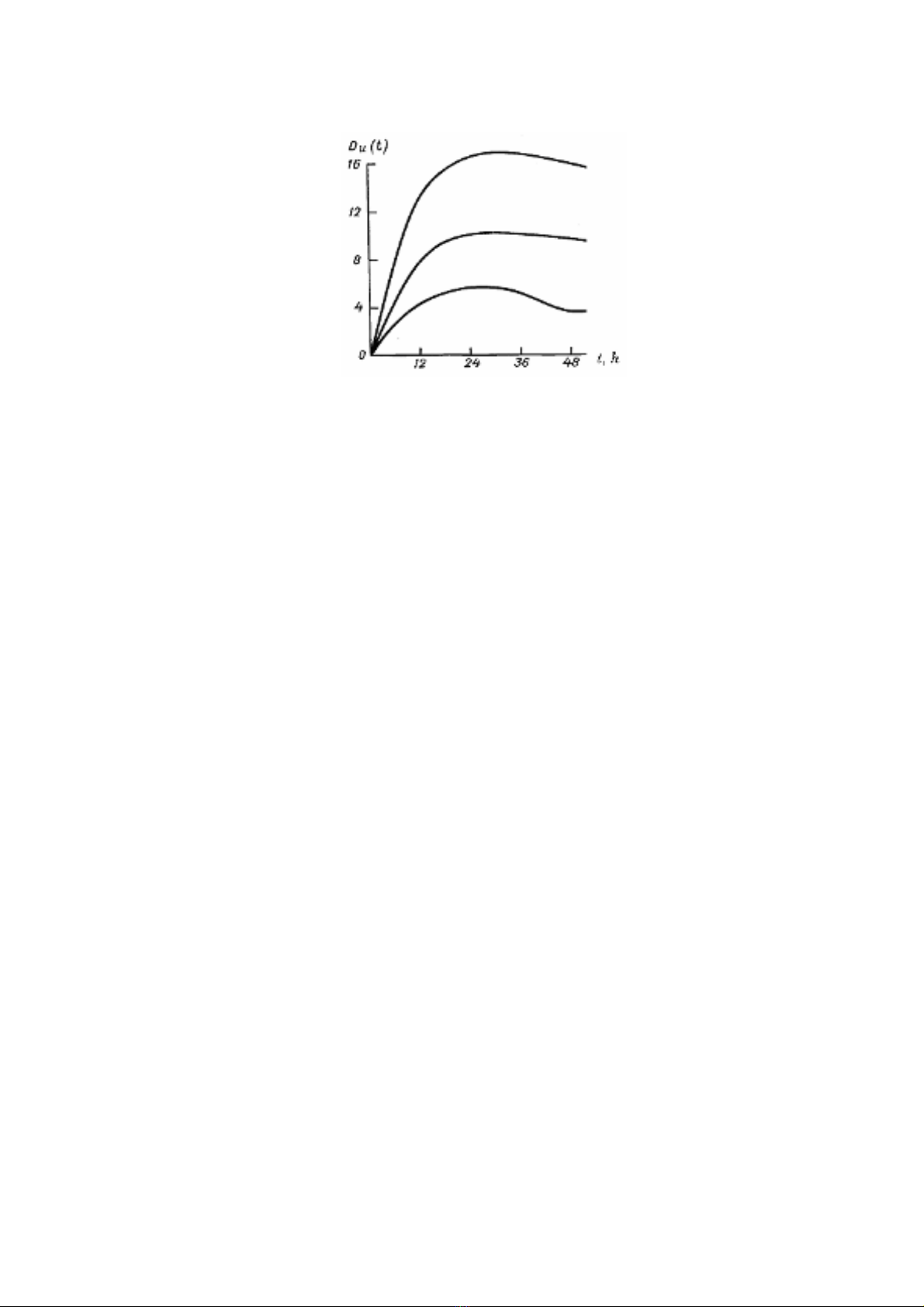
C¸c gi¸ trÞ cña hÖ sè khuÕch t¸n rèi cña thμnh phÇn vÜ h−íng ®· ®−îc tÝnh vμ dÉn
ra trªn h×nh 10.2.
Ph©n tÝch h×nh nμy cho thÊy r»ng, theo thêi gian hÖ sè khuÕch t¸n rèi t¨ng lªn, ®¹t
®Õn cùc ®¹i sau 30 giê, sau ®ã dÇn tiÕn ®Õn gi¸ trÞ giíi h¹n
∞
ττ=∞
0
dRD u)()( ,
mμ trªn thùc tÕ nã ®¹t ®−îc chØ ë kho¶ng 6054 ÷=τ giê.
Ch−¬ng 11: VÒ viÖc tÝnh mËt ®é phæ qu¸ tr×nh ngÉu nhiªn dõng.
Phæ sãng biÓn
11.1. X¸c ®Þnh mËt ®é phæ theo sè liÖu thùc nghiÖm
Trong ch−¬ng 3 chóng ta ®· thÊy mËt ®é phæ )(
ω
S cña qu¸ tr×nh ngÉu nhiªn dõng
lμ biÕn ®æi Fourier hμm t−¬ng quan )(τR cña nã vμ cã thÓ ®−îc x¸c ®Þnh theo c«ng thøc
(3.2.12). Khi ®ã cÇn biÕt hμm t−¬ng quan thùc trªn toμn kho¶ng v« h¹n cña sù biÕn ®æi
cña ®èi sè.
Khi x¸c ®Þnh nh÷ng ®Æc tr−ng thèng kª cña qu¸ tr×nh ngÉu nhiªn )(tX theo sè liÖu
thùc nghiÖm chóng ta sö dông c¸c thÓ hiÖn cña qu¸ tr×nh ngÉu nhiªn ®−îc ghi trªn mét
kho¶ng h÷u h¹n
T
nμo ®ã cña sù biÕn thiªn cña ®èi sè t. Khi ®ã ta cã thÓ x¸c ®Þnh gi¸ trÞ
thèng kª cña hμm t−¬ng quan )(
~τR trªn kho¶ng
[]
TT ,−∈τε. §Æc biÖt, khi x¸c ®Þnh hμm
t−¬ng quan cña qu¸ tr×nh ngÉu nhiªn dõng cã tÝnh egodic theo mét thÓ hiÖn )(tx ®é dμi
T
, gi¸ trÞ thèng kª cña nã ®−îc x¸c ®Þnh theo c«ng thøc (2.6.2).
Nh− ®· thÊy trong ch−¬ng 6, do nhiÒu nguyªn nh©n, gi¸ trÞ thèng kª cña hμm t−¬ng
207
quan lμ mét hμm ngÉu nhiªn nμo ®ã, vμ gi¸ trÞ tÝnh ®−îc cña nã )(
~
τR cã thÓ kh¸c nhiÒu so
víi gi¸ trÞ thùc cña hμm t−¬ng quan )(τR vμ ph−¬ng sai sai sè t¨ng ®¸ng kÓ khi ®èi sè τ
t¨ng.
V× vËy viÖc sö dông trùc tiÕp c«ng thøc (3.2.12) vμ thay hμm t−¬ng quan thùc trong
®ã b»ng gi¸ trÞ thèng kª cña nã, thay kho¶ng tÝch ph©n v« h¹n b»ng kho¶ng h÷u h¹n, tøc
c«ng thøc
−
ωτ−ττ
π
=ω
T
T
idReS )(
~
)(
~
2
1,
lμ kh«ng hîp lý, v× viÖc kh«ng tÝnh ®Õn nh÷ng trÞ sè cña hμm t−¬ng quan khi T>τ
vμ nh÷ng kh¸c biÖt ®¸ng kÓ cña hμm )(
~τR so víi gi¸ trÞ thùc cña hμm t−¬ng quan, ®Æc
biÖt t¹i nh÷ng gi¸ trÞ τ gÇn c¸c cËn cña kho¶ng tÝch ph©n, cã thÓ dÉn ®Õn gi¸ trÞ )(
~ωS
t×m ®−îc sÏ rÊt kh¸c víi gi¸ trÞ thùc cña mËt ®é phæ.
Mét vÊn ®Ò n¶y sinh lμ, lμm thÕ nμo ®Ó x¸c ®Þnh gi¸ trÞ phï hîp nhÊt cña mËt ®é phæ
cña qu¸ tr×nh ngÉu nhiªn ®ang xÐt trong khi kh«ng cã hμm t−¬ng quan thùc, mμ chØ sö
dông gi¸ trÞ thèng kª cña nã.
Ta xÐt hμm )(
~τR, b»ng gi¸ trÞ thùc cña hμm t−¬ng quan )(τR khi m
τ≤τ vμ b»ng 0
khi m
τ>τ . Hμm nμy cã thÓ xem nh− tÝch cña hμm )(τR víi hμm )(τλ
)()()(
~ττλ=τ RR , (11.1.1)
trong ®ã
τ>τ
τ≤τ
=τλ .
,
)(
m
m
khi 0
khi 1 (11.1.2)
Hμm )(
~τR ®−îc cho trªn kh¾p trôc sè thùc. Ta sÏ t×m biÕn ®æi Fourier cña nã vμ
xem ®ã lμ gi¸ trÞ gÇn ®óng )(
~ωS cña mËt ®é phæ )(
ω
S, tøc lμ tÝnh )(
~ωS theo c«ng thøc
∞
∞−
ωτ−
∞
∞−
ωτ−τττλ
π
=ττ
π
=ω dRedReS ii )()()(
~
)(
~
2
1
2
1. (11.1.3)
Ta ký hiÖu )(
ω
S lμ mËt ®é phæ thùc cña qu¸ tr×nh ngÉu nhiªn, tøc biÕn ®æi Fourier
cña hμm t−¬ng quan thùc )(τR, ký hiÖu )(
ω
Q lμ biÕn ®æi Fourier, tøc phæ, cña hμm )(τλ
ττλ
π
=ω
∞
∞−
ωτ−deQ i)()( 2
1. (11.1.4)
Theo (11.1.3) tÝch )()( ττλ R lμ biÕn ®æi Fourier cña hμm )(
~ωS
ωω=ττλ
∞
∞−
ωτ dSeR i)(
~
)()( . (11.1.5)
MÆt kh¸c, ta cã
=ωωωω=ττλ ∞
∞−
τω
∞
∞−
τω
2211 21 dQedSeR ii )()()()(
1221 22 ω
ωωω= 
∞
∞−
∞
∞−
τω+ω ddQeS i)()( )( .
Khi thay thÕ ω=ω+ω 21 ë tÝch ph©n bªn trong vμ ®æi thø tù lÊy tÝch ph©n, ta ®−îc
208

∞
∞−
∞
∞−
ωτ ω
ωω−ωω=ττλ ddQSeR i 111 )()()()( . (11.1.6)
So s¸nh (11.1.5) vμ (11.1.6) ta nhËn ®−îc mèi liªn hÖ gi÷a mËt ®é phæ thùc )(
ω
S vμ
gi¸ trÞ gÇn ®óng cña nã (11.1.3)
∞
∞−
ωω−ωω=ω 111 dQSS )()()(
~. (11.1.7)
Tõ ®ã thÊy r»ng, )(
~ωS chÝnh lμ gi¸ trÞ cña mËt ®é phæ thùc )(
ω
S ®−îc lÊy trung
b×nh theo toμn kho¶ng tÇn víi hμm träng l−îng )( 1
ω−ωQ.
§èi víi hμm )(τλ d¹ng (11.1.2) phæ )(
ω
Q cña nã ®−îc x¸c ®Þnh d−íi d¹ng
τ
τ−
ωτ−
πω
ωτ
=τ
π
=ω
m
m
m
ideQ sin
)( 2
1. (11.1.8)
Nh− vËy, b»ng c¸ch sö dông tÝch (11.1.1) lμm gi¸ trÞ thèng kª cña hμm t−¬ng quan
trong khi x¸c ®Þnh mËt ®é phæ, chóng ta nhËn ®−îc kh«ng ph¶i mËt ®é phæ thùc )(
ω
S,
mμ gi¸ trÞ cña nã ®−îc lμm tr¬n nhê hμm träng l−îng lμ phæ cña hμm )(τλ . Khi ®ã
ph−¬ng ph¸p lμm tr¬n ®−îc x¸c ®Þnh b»ng c¸ch chän hμm )(τλ . Tõ ®ã n¶y sinh ý t−ëng
lùa chän hμm )(τλ sao cho phÐp lμm tr¬n (11.1.7) lμ tèt nhÊt, tøc nã cho gi¸ trÞ )(
~ωS gÇn
nhÊt víi gi¸ trÞ thùc )(
ω
S.
Nh− vËy bμi to¸n x¸c ®Þnh mËt ®é phæ cã thÓ ph¸t biÓu d−íi d¹ng sau: Gi¶ sö cã gi¸
trÞ thèng kª cña hμm t−¬ng quan )(
~τR t¹i T≤τ , ta sÏ t×m gi¸ trÞ thèng kª cña mËt ®é
phæ )(
~ωS theo c«ng thøc
τ
τ−
ωτ−τττλ
π
=ω
m
m
dReS i)(
~
)()(
~
2
1 (11.1.9)
víi ®iÒu kiÖn ph¶i chän hμm )(τλ vμ gi¸ trÞ m
τ sao cho tho¶ m·n mét chØ tiªu tèi −u nμo
®ã. Hμm )(τλ ®−îc gäi lμ hμm träng l−îng lμm tr¬n, cßn gi¸ trÞ m
τ gäi lμ ®iÓm c¾t cña
hμm t−¬ng quan.
ý nghÜa cña hμm )(τλ ë chç, nhê nã ng−êi ta lμm tr¬n gi¸ trÞ thèng kª cña hμm
t−¬ng quan ®Ó tõ ®ã x¸c ®Þnh mËt ®é phæ. Nh− ta ®· thÊy, viÖc chän hμm lμm tr¬n )(τλ
t−¬ng øng víi sù lμm tr¬n phæ thùc cña qu¸ tr×nh ngÉu nhiªn d¹ng (11.1.7) víi hμm
träng l−îng lμ phæ cña hμm )(τλ .
§Ó lμm tiªu chuÈn ®¸nh gi¸ ®¹i l−îng )(
~ωS vμ chän hμm lμm tr¬n tèi −u )(τλ cã thÓ
lÊy sai sè b×nh ph−¬ng trung b×nh )](
~
[ωη S, x¸c ®Þnh theo c«ng thøc
[] [ ]
{
}
[][]
)(
~
)(
~
)()(
~
)(
~
ω+ωσ=ω−ω=ωη SbSSSMS 22
2
2 . (11.1.10)
Trong c«ng thøc nμy ®¹i l−îng
[] [][]
{
}
[][]
)(
~
)(
~
)(
~
)(
~
)(
~ω−ωσ=ω−ω=ωσ SbSSMSMS 22
2
2 (11.1.11)
lμ ph−¬ng sai cña c¸c gi¸ trÞ )(
~ωS vμ ®Æc tr−ng cho sù t¶n m¹n cña c¸c gi¸ trÞ thèng kª cña
mËt ®é phæ xung quanh kú väng to¸n häc cña nã.
§¹i l−îng
)()(
~
)(
~ω−ω=ω SSMSb2 (11.1.12)
209
®−îc gäi lμ ®é chÖch vμ ®Æc tr−ng cho sù lÖch cña kú väng to¸n häc cña c¸c trÞ sè thèng kª
)(
~ωSkhái gi¸ trÞ thùc )(
ω
S. §é chÖch ®Æc tr−ng cho sù hiÖn diÖn cña sai sè hÖ thèng, v×
nã mμ c¸c gi¸ trÞ )(
~ωS sÏ tËp trung kh«ng ph¶i gÇn gi¸ trÞ thùc )(
ω
S, mμ gÇn mét gi¸ trÞ
)](
~
[ωSM nμo ®ã.
Tiªu chuÈn kh¸c, nhê ®ã cã thÓ ®¸nh gi¸ ®é chÝnh x¸c cña viÖc x¸c ®Þnh ®¹i l−îng
)(
~ωS vμ chän hμm lμm tr¬n tèi −u )(τλ , lμ sai sè b×nh ph−¬ng trung b×nh tÝch ph©n
[]
ωω−ω=ω
∞
∞−
dSSMSJ
2
)()(
~
)(
~. (11.1.13)
Bμi to¸n chän hμm lμm tr¬n tèi −u lμ lμm sao víi gi¸ trÞ ®é dμi kho¶ng
T
®· cho,
ph¶i chän mét hμm )(τλ lμm cho ®é lín cña tiªu chuÈn ®¸nh gi¸ ®· chän trë thμnh cùc
tiÓu. NghiÖm cña bμi to¸n nμy phô thuéc nhiÒu vμo d¹ng cña hμm t−¬ng quan thùc )(τR.
Trong c«ng tr×nh cña E. Parzen [70] ®· nhËn ®−îc nghiÖm bμi to¸n nμy øng víi tiªu
chuÈn (11.1.13) cho hai d¹ng hμm t−¬ng quan )(τR.
D¹ng thø nhÊt gåm líp c¸c hμm t−¬ng quan gi¶m theo quy luËt hμm mò víi hÖ sè
,0>
ρ
tøc nh÷ng hμm tho¶ m·n bÊt ®¼ng thøc τρ−
≤τ eRR 0
)( , trong ®ã 0
R lμ mét h»ng sè
nμo ®ã.
Ng−êi ta ®· chøng minh ®−îc r»ng ®èi víi nh÷ng hμm t−¬ng quan nh− vËy c¸c hμm
lμm tr¬n sau lμ tèi −u:
,
sin
)(,)(,)( u
u
u
uu
u=τλ
>
≤−
=τλ
+
=τλ
1 khi0
1 khi1
1
1
τ
τ
=
m
u,
vμ mét sè hμm kh¸c n÷a.
D¹ng thø hai c¸c hμm t−¬ng quan mμ Parzen xÐt lμ líp c¸c hμm gi¶m theo kiÓu ®¹i
sè, tøc nh÷ng hμm cã d¹ng
r−
τtrong ®ã 1<
r
víi nh÷ng gi¸ trÞ τ lín. §èi víi c¸c hμm
d¹ng nμy nh÷ng hμm träng l−îng tèi −u lμm cho sai sè b×nh ph−¬ng trung b×nh tÝch ph©n
cùc tiÓu cã thÓ lμ nh÷ng hμm d¹ng
r
Bu2
1
1
+
=τλ )( ,
trong ®ã h»ng sè B ®−îc biÓu diÔn qua hμm t−¬ng quan thùc )(τR.
Lomnhisky vμ Zaremba [96] ®· chøng minh r»ng hμm träng l−îng tèi −u )(τλ lμm
cho sai sè b×nh ph−¬ng trung b×nh tÝch ph©n (11.1.13) cùc tiÓu, cã d¹ng
[]
)(
~
)(
)(
)( τ+τ
τ
=τλ RDR
R
2
2. (11.1.14)
§iÒu nμy cho thÊy r»ng hμm lμm tr¬n tèi −u )(τλ phô thuéc vμo hμm t−¬ng quan
thùc cña qu¸ tr×nh ngÉu nhiªn ®−îc kh¶o s¸t vμ do ®ã, kh«ng tån t¹i mét hμm lμm tr¬n
duy nhÊt ¸p dông cho tÊt c¶ c¸c qu¸ tr×nh ngÉu nhiªn.
Ngoμi ra, v× khi x¸c ®Þnh thùc nghiÖm c¸c ®Æc tr−ng thèng kª cña qu¸ tr×nh ngÉu
nhiªn ta ch−a biÕt hμm t−¬ng quan thùc, cßn gi¸ trÞ thèng kª cña nã chØ lμ −íc l−îng gÇn
®óng, nªn ta kh«ng thÓ sö dông trùc tiÕp c¸c c«ng thøc ®· dÉn ®Ó x¸c ®Þnh hμm )(τλ .
Nh÷ng c«ng thøc nμy chØ cã thÓ sö dông nh− lμ c«ng thøc ®Þnh h−íng khi chän d¹ng cô
thÓ cña hμm lμm tr¬n trong c«ng thøc (11.1.9).
210
HiÖn nay c¸c t¸c gi¶ kh¸c nhau ®Ò x−íng nhiÒu d¹ng hμm lμm riªng biÖt cã nh÷ng
tÝnh chÊt kh¸c nhau, m« t¶ chi tiÕt vÒ c¸c hμm nμy tr×nh bμy trong c¸c c«ng tr×nh [2, 25,
70, 91−97].
Phæ dông nhÊt trong sè ®ã lμ nh÷ng hμm sau:
1. Hμm Bartlette
τ>τ
τ≤τ
=τλ .
,
)(
m
m
khi0
khi1 (11.1.15)
2. Hμm Bartlette biÕn d¹ng
τ>τ
τ≤τ
τ
τ
−
=τλ
.
,
)(
m
m
m khi0
khi1 (11.1.16)
3. Hμm Tiukey
τ>τ
τ≤τ
τ
πτ
+−
=τλ
.
,cos
)(
m
m
m
aa
khi0
khi221 (11.1.17)
Tiukey ®Ò nghÞ lÊy hÖ sè 230,=a mμ kh«ng chØ râ lý do chän trÞ sè ®ã. Parzen cho
biÕt r»ng trÞ sè 250,=a lμ tèi −u d−íi gãc ®é tiªu chuÈn (11.1.13).
4. Hμm Hanning
τ>τ
τ≤τ
τ
πτ
−
=τλ
.
,cos,
)(
m
m
m
khi0
khi150 (11.1.18)
5. Hμm Parzen
τ>τ
τ≤τ
τ
τ
−
=τλ
.
,
)(
m
m
q
m
khi0
khi1 (11.1.19)
víi 1,>q®Æc biÖt Parzen ®· xÐt hμm nμy víi .2=q
6. Parzen còng ®· nghiªn cøu hμm d¹ng
τ>τ
τ≤τ
τ
τ
+
=τλ
,
,
)(
m
m
q
m
khi0
khi
1
1
(11.1.20)
®èi víi nh÷ng trÞ sè 1=q vμ .2=q
7. Hμm Hemming
τ>τ
τ≤τ
τ
πτ
+
=τλ
.
,cos,,
)(
m
m
m khi0
khi460540 (11.1.21)
TÊt c¶ nh÷ng hμm ®· tr×nh bμy lμ tèt nhÊt theo quan ®iÓm tèi −u ho¸ mét tÝnh chÊt
nμo ®ã trong sè c¸c tÝnh chÊt cña gi¸ trÞ thèng kª cña mËt ®é phæ.
Khi x¸c ®Þnh gi¸ trÞ thèng kª cña mËt ®é phæ theo c«ng thøc (11.1.9) víi hμm lμm