104
Ch−¬ng 4: BiÕn ®æi tuyÕn tÝnh qu¸ tr×nh ngÉu nhiªn dõng
4.1. BiÕn ®æi hμm ngÉu nhiªn b»ng to¸n tö tuyÕn tÝnh
Gi¶ sö hμm ϕ(t) nhËn ®−îc tõ hμm f(t) b»ng c¸ch thùc hiÖn mét sè phÐp to¸n nμo ®ã
vμ L lμ ký hiÖu qui −íc c¸c phÐp to¸n nμy, tøc L lμ qui t¾c, theo ®ã hμm f(t) biÕn ®æi
thμnh ϕ(t). Trong to¸n häc, ng−êi ta gäi qui t¾c, theo nã mét tËp hμm ®−îc ¸nh x¹ sang
mét tËp hîp hμm kh¸c lμ to¸n tö. Ta sÏ nãi r»ng, hμm ϕ(t) lμ kÕt qu¶ t¸c dông to¸n tö L
lªn hμm f(t), tøc lμ
() (){}
tfLt =
ϕ
. (4.1.1)
Trong kü thuËt v« tuyÕn vμ c¸c øng dông kü thuËt kh¸c ng−êi ta th−êng gäi hμm
f(t) lμ t¸c dông lèi vμo, hμm ϕ(t) lμ tÝn hiÖu ra, cßn L to¸n tö cña hÖ lμm biÕn ®æi t¸c dông
lèi vμo. To¸n tö L ®−îc gäi lμ tuyÕn tÝnh, nÕu nã tho¶ m·n hai ®iÒu kiÖn sau:
1.
(){} (){}
xfcLxcfL = (4.1.2)
tøc lμ kÕt qu¶ t¸c dông to¸n tö lªn tÝch cña hμm f(t) vμ mét thõa sè kh«ng ®æi c b»ng tÝch
cña thõa sè ®ã víi kÕt qu¶ t¸c dông to¸n tö ®ã lªn f(t).
2.
() (){}(){} (){}
tfLtfLtftfL 2121 +=+ (4.1.3)
tøc lμ kÕt qu¶ t¸c dông to¸n tö lªn tæng hai hμm b»ng tæng kÕt qu¶ t¸c dông to¸n tö lªn
mçi hμm riªng biÖt.
To¸n tö kh«ng tho¶ m·n c¸c ®iÒu kiÖn trªn gäi lμ to¸n tö phi tuyÕn.
VÝ dô, to¸n tö vi ph©n lμ to¸n tö tuyÕn tÝnh, v× nã tho¶ m·n c¸c ®¼ng thøc
(){} (){}
tf
dt
d
ctcf
dt
d
11 =
vμ
() (){}(){} (){}
tf
dt
d
tf
dt
d
tftf
dt
d
2121 +=+ .
To¸n tö lÊy tÝch ph©n lμ to¸n tö tuyÕn tÝnh. To¸n tö nhËn ®−îc khi t¸c dông liªn
tiÕp mét vμi to¸n tö tuyÕn tÝnh còng lμ to¸n tö tuyÕn tÝnh. To¸n tö lÊy kú väng to¸n häc
cña hμm ngÉu nhiªn lμ to¸n tö tuyÕn tÝnh.
VÝ dô vÒ to¸n tö phi tuyÕn lμ phÐp to¸n n©ng lªn luü thõa, to¸n tö lÊy ph−¬ng sai
hμm ngÉu nhiªn.
NÕu hμm ngÉu nhiªn Y(t) lμ kÕt qu¶ t¸c dông cña mét to¸n tö tuyÕn tÝnh L bÊt kú
lªn hμm ngÉu nhiªn X(t) cã kú väng to¸n häc mx(t) vμ hμm t−¬ng quan Rx(t1,t2), tøc lμ
() (){}
tXLtY = (4.1.4)
th×
() (){}
tmLtm xy = (4.1.5)
()
()( )
(){}
2121 ,, 21 ttRLLttR x
tt
y= (4.1.6)
nghÜa lμ my(t) nhËn ®−îc b»ng c¸ch t¸c dông to¸n tö L lªn mx(t), Ry(t1,t2) nhËn ®−îc b»ng
c¸ch t¸c dông hai lÇn to¸n tö L lªn hμm Rx(t1,t2), ®Çu tiªn theo ®èi sè thø nhÊt t1, sau ®ã
theo ®èi sè thø hai t2.
105
Thùc vËy,
() (){}
[]
tXLMtmy= (4.1.7)
To¸n tö L t¸c dông lªn biÕn t, to¸n tö t×m kú väng to¸n häc tiÕn hμnh lÊy trung
b×nh tung ®é cña hμm ngÉu nhiªn (khi cè ®Þnh t) theo tËp hîp tÊt c¶ c¸c gi¸ trÞ cã thÓ cña
®¹i l−îng ngÉu nhiªn X(t), còng lμ to¸n tö tuyÕn tÝnh. V× vËy, cã thÓ ®æi chç trËt tù t¸c
dông cña c¸c to¸n tö M vμ L cho nhau, tøc lμ my(t)= L{M[X(t)]}=L{mx(t)}, vμ ®iÒu ®ã ®·
chøng minh cho ®¼ng thøc (4.1.5).
TiÕp theo
( ) () ()
[
]
() ()
[
]
{
}
221121,tmtYtmtYMttR yyy −−= =
()
(){}
()
(){}
(
)
()
(){}
()
(){}
(
)
[
]
2211
21211 tmLtXLtmLtXLM x
tt
x
tt −−= =
() ( )
() ()
[]
() ()
[]
{}
[
2211
21 tmtXtmtXLLM xx
tt −−= =
() ( )
() ()
[]
() ()
[][]
{}
2211
21 tmtXtmtXMLL xx
tt −−=
()( )
(){}
21,
21 ttRLL x
tt
=.
C¸c c«ng thøc ®· tr×nh bμy trong ch−¬ng 2 ®èi víi kú väng to¸n häc vμ hμm t−¬ng
quan cña ®¹o hμm vμ tÝch ph©n cña hμm ngÉu nhiªn lμ c¸c tr−êng hîp riªng cña (4.1.5)
vμ (4.1.6).
ViÖc biÕt Dx(t) lμ ch−a ®ñ ®Ó nhËn ®−îc ph−¬ng sai Dy(t) cña qu¸ tr×nh ngÉu nhiªn
Y(t). Tr−íc hÕt cÇn ph¶i t×m hμm t−¬ng quan Ry(t1,t2) theo c«ng thøc (4.1.6), sau ®ã thÕ
vμo nã t1=t2=t.
§Ó t×m c¸c ®Æc tr−ng cña hμm ngÉu nhiªn, lμ kÕt qu¶ t¸c dông to¸n tö phi tuyÕn
lªn hμm ngÉu nhiªn X(t), th× biÕt mx(t) vμ Rx(t1,t2) còng ch−a ®ñ, v× trong tr−êng hîp nμy
qui luËt ph©n bè cña hμm X(t) ®ãng mét vai trß quan träng. §èi víi c¸c to¸n tö phi tuyÕn
cã thÓ nhËn ®−îc nh÷ng kÕt qu¶ t−¬ng ®èi ®¬n gi¶n chØ ë trong mét sè tr−êng hîp riªng.
Trong tr−êng hîp t¸c dông to¸n tö tuyÕn tÝnh lªn hμm X(t) cã qui luËt ph©n bè
chuÈn, hμm ngÉu nhiªn Y(t) = L{X(t)} còng tu©n theo qui luËt ph©n bè chuÈn, bëi v× do
tÝnh chÊt tuyÕn tÝnh cña to¸n tö L, hμm Y(t) cã thÓ chØ nhËn ®−îc nhê tæ hîp tuyÕn tÝnh
cña mét sè h÷u h¹n hoÆc v« h¹n c¸c tung ®é cña hμm X(t). Nh−ng tõ lý thuyÕt x¸c suÊt
ta biÕt r»ng, tæ hîp tuyÕn tÝnh c¸c ®¹i l−îng ngÉu nhiªn ph©n bè chuÈn phô thuéc hoÆc
®éc lËp ®Òu tu©n theo qui luËt ph©n bè chuÈn.
Do vËy, trong tr−êng hîp X(t) lμ hμm ngÉu nhiªn tu©n theo qui luËt ph©n bè chuÈn,
th× Y(t) còng tu©n theo qui luËt ph©n bè chuÈn vμ c¸c ®Æc tr−ng my(t), Ry(t1,t2) t×m ®−îc
hoμn toμn x¸c ®Þnh nã.
NÕu X(t) kh«ng ph¶i lμ hμm ngÉu nhiªn ph©n bè chuÈn, th× Y(t) còng sÏ kh«ng cã
cïng qui luËt ph©n bè víi X(t). Qui luËt ph©n bè chuÈn còng sÏ kh«ng ®−îc b¶o toμn nÕu
to¸n tö L kh«ng tuyÕn tÝnh.
4.2. BiÕn ®æi tuyÕn tÝnh d−íi d¹ng phæ
Ta h·y biÓu diÔn phÐp biÕn ®æi tuyÕn tÝnh d−íi d¹ng phæ. Muèn vËy, ta sö dông
kh¸i niÖm hμm delta Dirac, mét hμm ®−îc sö dông réng r·i trong to¸n häc.
Hμm delta δ(t) lμ hμm cã c¸c tÝnh chÊt sau:
106
1)
()
=∞
≠
=0
00
t
t
t
δ
(4.2.1)
tøc lμ δ(t) b»ng kh«ng víi mäi gi¸ trÞ t kh¸c kh«ng, cßn t¹i ®iÓm t = 0 th× t¨ng lªn v« h¹n.
2) TÝch ph©n hμm delta trªn toμn miÒn v« h¹n b»ng ®¬n vÞ
()
1=
∞
∞−
dtt
δ
(4.2.2)
Hμm delta kh«ng ph¶i lμ hμm theo
nghÜa th«ng th−êng, mμ lμ mét hμm
t−îng tr−ng nμo ®ã. Theo nghÜa chÝnh
x¸c, hμm cã c¸c tÝnh chÊt (4.2.1) vμ
(4.2.2) kh«ng tån t¹i. Tuy nhiªn cã thÓ
xÐt hμm δ(t) theo mét nghÜa nμo ®ã
gièng nh− giíi h¹n cña hμm th«ng
th−êng.
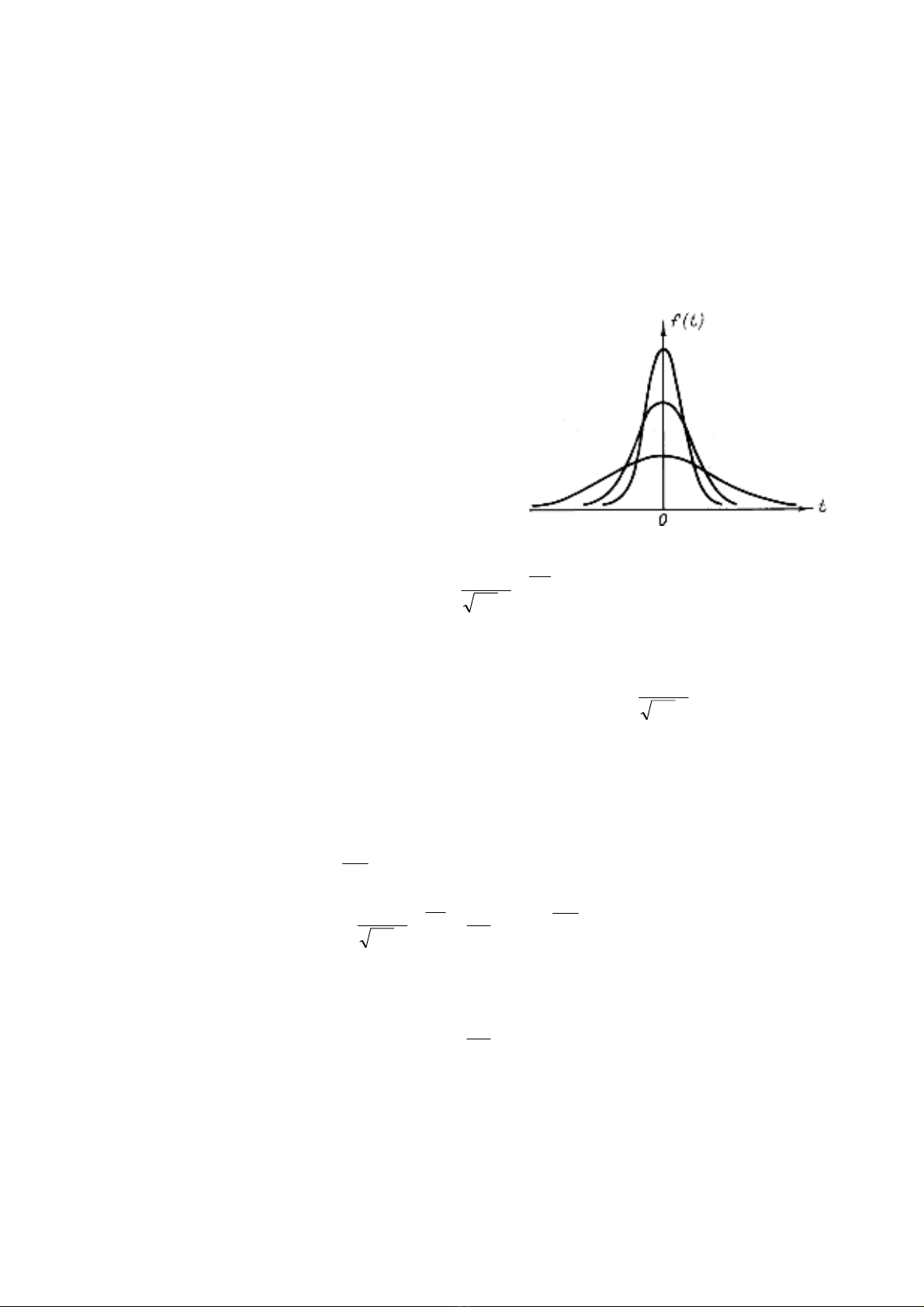
Ta lÊy hμm Gauss lμm vÝ dô
H×nh 4.1
()
2
2
2
2
1
σ
σπ
t
etf
−
=,
®èi víi hμm nμy hÖ thøc (4.2.2) ®−îc tho¶ m·n.
Ta sÏ gim ®¹i l−îng σ xuèng, khi ®ã ®å thÞ cña hμm sÏ nhän h¬n (trong nguyªn
b¶n viÕt lμ ®å thÞ gi·n ra −ND) (h×nh 4.1), gi¸ trÞ cùc ®¹i
()
σπ
2
1
0=f sÏ t¨ng, cßn miÒn
gi¸ trÞ kh¸c kh«ng cña hμm thu hÑp l¹i. LÊy giíi h¹n khi σ→0 ta nhËn ®−îc hμm cã tÝnh
chÊt cña hμm delta.
Sö dông kh¸i niÖm giíi h¹n nμy, cã thÓ biÓu diÔn hμm delta d−íi d¹ng tÝch ph©n.
T−¬ng øng víi môc 1.12, mËt ®é ph©n bè cña ®¹i l−îng ngÉu nhiªn ph©n bè chuÈn cã thÓ
®−îc biÓu diÔn nh− lμ phÐp biÕn ®æi ng−îc Fourier hμm ®Æc tr−ng cña nã, theo (1.12.25)
hμm nμy cã d¹ng
()
2
22
σω
ω
−
=eg . Do tÝnh ch½n cña hμm nμy nªn ta cã ®¼ng thøc
∞
∞−
−
−
−=
ω
π
σπ
σω
ω
σ
deee ti
t
2
2
22
2
2
2
1
2
1 (4.2.3)
LÊy giíi h¹n hai vÕ ®¼ng thøc (4.2.3) khi σ→0 ta nhËn ®−îc biÓu diÔn tÝch ph©n
hμm delta
∞
∞−
−
=
ω
π
δ
ω
det ti
2
1
)( (4.2.4)
NÕu xÐt hμm delta cña ®èi sè t−τ, víi τ lμ mét sè x¸c ®Þnh, th×
()
=∞
≠
=−
τ
τ
τδ
t
t
t0 (4.2.5)
107
()
1=−
∞
∞−
dtt
τδ
(4.2.6)
§èi víi mäi hμm f(t) bÊt kú, liªn tôc t¹i t=τ, ta cã ®¼ng thøc
()( ) ()
tfdtf =−
∞
∞−
ττδτ
(4.2.7)
§iÒu nμy ®−îc suy ra mét c¸ch ®¬n gi¶n nh− sau, mÆc dï kh«ng thËt chÆt chÏ. V×
δ(t−τ) kh¸c 0 chØ khi t=τ, nªn tÝch ph©n (4.2.7) kh¸c 0 chØ trong kho¶ng [t−ε, t+ε], víi ε>0
bÐ tuú ý. Tõ ®ã
()( ) ()( )
+
−
∞
∞−
−=−
ε
ε
ττδτττδτ
t
t
dtfdtf
() ( ) () ( ) ()
tfdttfdttf
t
t
=ττ−δ=ττ−δ= ∞
∞−
ε+
ε−
Ký hiÖu g(t,τ) lμ kÕt qu¶ t¸c dông to¸n tö tuyÕn tÝnh L nμo ®ã lªn hμm delta δ(t−τ)
t¹i ®iÓm τ cè ®Þnh
() ( ){}
τ
δ
τ
−= tLtg ,. (4.2.8)
Nhê hμm g(t,τ) nμy, ta sÏ biÓu thÞ kÕt qu¶ t¸c dông to¸n tö L ®· cho lªn hμm f(t)
bÊt kú cho trªn ®o¹n [a,b].
T¸c dông to¸n tö tuyÕn tÝnh L lªn hai vÕ ®¼ng thøc (4.2.7), ta ®−îc
(){} ()()
=
b
a
dftgtfL
τττ
, (4.2.9)
Nh− vËy, hμm ϕ(t)=L{f(t)}, kÕt qu¶ t¸c dông to¸n tö tuyÕn tÝnh L lªn hμm f(t), cã
thÓ ®−îc biÓu diÔn d−íi d¹ng
() ( ) ( )
=
b
a
dftgt
τττϕ
, (4.2.10)
Hμm g(t,τ), kÕt qu¶ t¸c dông to¸n tö L lªn hμm delta δ(t−τ), ®−îc gäi lμ hμm träng
l−îng. (Trong kü thuËt v« tuyÕn ng−êi ta gäi nã lμ hμm chuyÓn xung).
NÕu hμm f(t) ®−îc cho trong kho¶ng v« h¹n (−∞, +∞) th× cã thÓ viÕt
() ( ) ( )
∞
∞−
=
τττϕ
dftgt , (4.2.11)
Trong tr−êng hîp riªng, nÕu to¸n tö L lμ dõng th× hμm träng l−îng chØ phô thuéc
vμo hiÖu t−τ. Khi ®ã cã thÓ viÕt
() ( ) ( )
∞
∞−
−=
τττϕ
dftgt (4.2.12)
TÝch ph©n (4.2.12) ®−îc gäi lμ tÝch ph©n chËp cña hμm f(t) vμ g(t).
Ký hiÖu Sf(ω) vμ Sϕ(ω) lμ biÕn ®æi Fourier (mËt ®é phæ) t−¬ng øng cña c¸c hμm f(t)
vμ ϕ(t). Khi ®ã ta cã:
() ( )
∞
∞−
=
ωω
ω
deStf ti
f (4.2.13)
108
() ( )
∞
∞−
=
ωωϕ
ω
ϕ
deSt ti (4.2.14)
§Æt c¸c biÓu thøc trªn vμo (4.2.12), ta nhËn ®−îc
() ( ) ()
∞
∞−
∞
∞−
∞
∞−
−=
τωωτωω
ωτω
ϕ
ddeStgdeS i
f
ti (4.2.15)
Thay ®æi thø tù lÊy tÝch ph©n trong tÝch ph©n hai líp vμ lμm phÐp ®æi biÕn t−τ=τ1,
ta ®−îc
() () ()
∞
∞−
∞
∞−
−
∞
∞−
=
ωττωωω
ωτ
ωω
ϕ
ddegeSdeS i
ti
f
ti
11
1 (4.2.16)
Ký hiÖu G(ω) lμ biÕn ®æi Fourier (mËt ®é phæ ) cña hμm träng l−îng g(t)
() ()
∞
∞−
−
=dtetgG ti
ω
π
ω
2
1 (4.2.17)
TÝch ph©n trong mãc vu«ng (4.2.16) b»ng 2πG(ω), tõ ®ã cã thÓ viÕt
() () ()
[]
∞
∞−
=− 02.
ωωπωω
ω
ϕ
deGSS ti
f (4.2.18)
§iÒu nμy chøng tá r»ng, biÕn ®æi ng−îc Fourier hμm
() () ()
π
ϕ
GSS f2− b»ng
0, vμ do ®ã ®¼ng thøc sau cÇn ®−îc tho¶ m·n
() () ()
ω
π
ω
ω
ϕ
GSS f2.=. (4.2.19)
Hμm:
() () ()
∞
∞−
−
== dtetgGL ti
ω
ωπω
2 (4.2.20)
®−îc gäi lμ hμm truyÒn cña to¸n tö tuyÕn tÝnh L. Tõ ®ã cã thÓ viÕt (4.2.19) d−íi d¹ng
() ()()
ω
ω
ω
ϕ
LSS f
= (4.2.21)
Nh− vËy, mËt ®é phæ Sϕ(ω), kÕt qu¶ cña viÖc t¸c dông to¸n tö tuyÕn tÝnh L lªn hμm
f(t), b»ng tÝch mËt ®é phæ Sf(ω) cña hμm f(t) vμ hμm truyÒn L(ω) cña to¸n tö.
4.3 MËt ®é phæ cña phÐp biÕn ®æi tuyÕn tÝnh qu¸ tr×nh
ngÉu nhiªn dõng
B©y giê ta xÐt qu¸ tr×nh ngÉu nhiªn dõng X(t) cã kú väng to¸n häc b»ng 0 vμ hμm
t−¬ng quan Rx(τ) cho tr−íc. Vμ gi¶ sö mét qu¸ tr×nh ngÉu nhiªn kh¸c Y(t) lμ kÕt qu¶ t¸c
dông to¸n tö tuyÕn tÝnh dõng L lªn qu¸ tr×nh ngÉu nhiªn X(t)
() (){}
tXLtY =. (4.3.1)
Khi ®ã ta cã thÓ biÓu diÔn qu¸ tr×nh ngÉu nhiªn Y(t) d−íi d¹ng
() ( ) ( )
∞
∞−
−=
τττ
dXtgtY (4.3.2)
víi g(t−τ) lμ hμm träng l−îng.