Lý thuyết mẫu – bài toán ước lượng điểm
Thống kê toán học là khoa học thu thập, tổ chức sắp xếp, tổng hợp, phân tích và
rút ra các kết luận từ các dữ liệu thực nghiệm. Đối tượng của thống kê toán được
chia làm hai lĩnh vực:
+ Thống kê mô tả: nội dung của nó gồm việc thu thập số liệu, tổ chức sắp xếp,
tổng hợp, phân tích và biểu diễn các số liệu thực nghiệm.
+ Các kết luận thống kê bao gồm: thiết kế các kết luận thống kê, kiểm định giả
thiết, xác định các quan hệ và lập các dự báo.
Một trong những bài toán đầu tiên của thống kê toán học là bài toán ước lượng
tham số của phân phối. Trước khi đề cập tới vấn đề đó, ta cần các khái niệm về
mẫu ngẫu nhiên, hàm phân phối mẫu và các số đặc trưng mẫu.
1. Mẫu ngẫu nhiên, hàm phân phối mẫu và các số đặc trưng mẫu
Mẫu ngẫu nhiên
Giả sử là một đại lượng chưa biết nào đó biến thiên trong tập U. Để xác định
được giá trị gần đúng của ta phải tiến hành thực nghiệm, chẳng hạn ta tiến hành
n thí nghiệm. Kết quả của các thí nghiệm này được đặc trưng bởi dãy n biến ngẫu
nhiên X1,…, Xn mà phân phối của chúng là F(x, ) phụ thuộc vào (thậm chí nó
còn phụ thuộc vào các tham số chưa biết khác).
Ta gọi (X1, X2,…, Xn) là một mẫu ngẫu nhiên từ phân phối F(x, ). Số n được gọi
là kích thước mẫu (hay cỡ mẫu). Giá trị của mẫu thường kí hiệu bằng chữ (x1,
x2,…, xn). Không gian Rn mà phần tử của nó là các điểm (X1, X2,…, Xn) được gọi
là không gian mẫu.
Chú ý: Thông thường ta hay xét (X1,X2,…,Xn) là dãy các biến ngẫu nhiên độc lập
có cùng phân phối.
Hàm phân phối mẫu
Giả sử (X1,X2,…,Xn) là mẫu ngẫu nhiên từ phân phối F(x, ).
Định nghĩa 1.1. Hàm phân phối mẫu được định nghĩa bởi
, x R
trong đó n là kích thước mẫu, m là số các giá trị mẫu Xi < x.
Ví dụ 1.2. Kiểm tra ngẫu nhiên 10 học sinh. Kết quả điểm là (3, 3, 4, 5, 5, 6, 6, 7,
7, 9). Viết hàm phân phối mẫu.
Giải. Hàm phân phối mẫu là
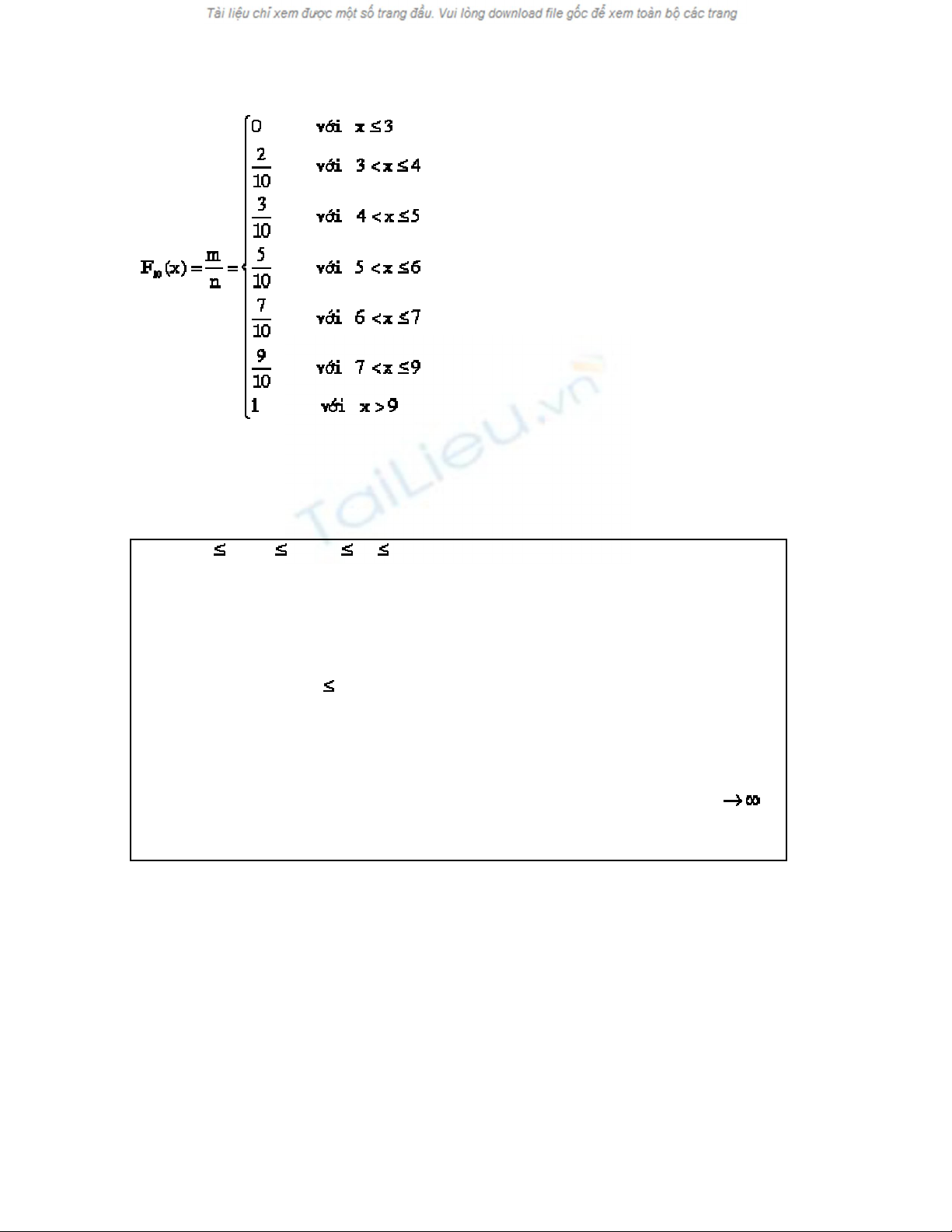
Tính chất 1.3. (Tính chất của hàm phân phối mẫu)
0 Fn(x) 1 vì 0 m n.
Fn(x) là hàm đơn điệu tăng.
Fn(x) = 0 với x min (X1,…, Xn) và Fn(x) = 1 với x > max (X1, X2,…,
Xn)
Fn(x) hội tụ hầu chắc chắn về hàm phân phối lí thuyết F(x) khi n
Các số đặc trưng mẫu
Ø Trung bình mẫu
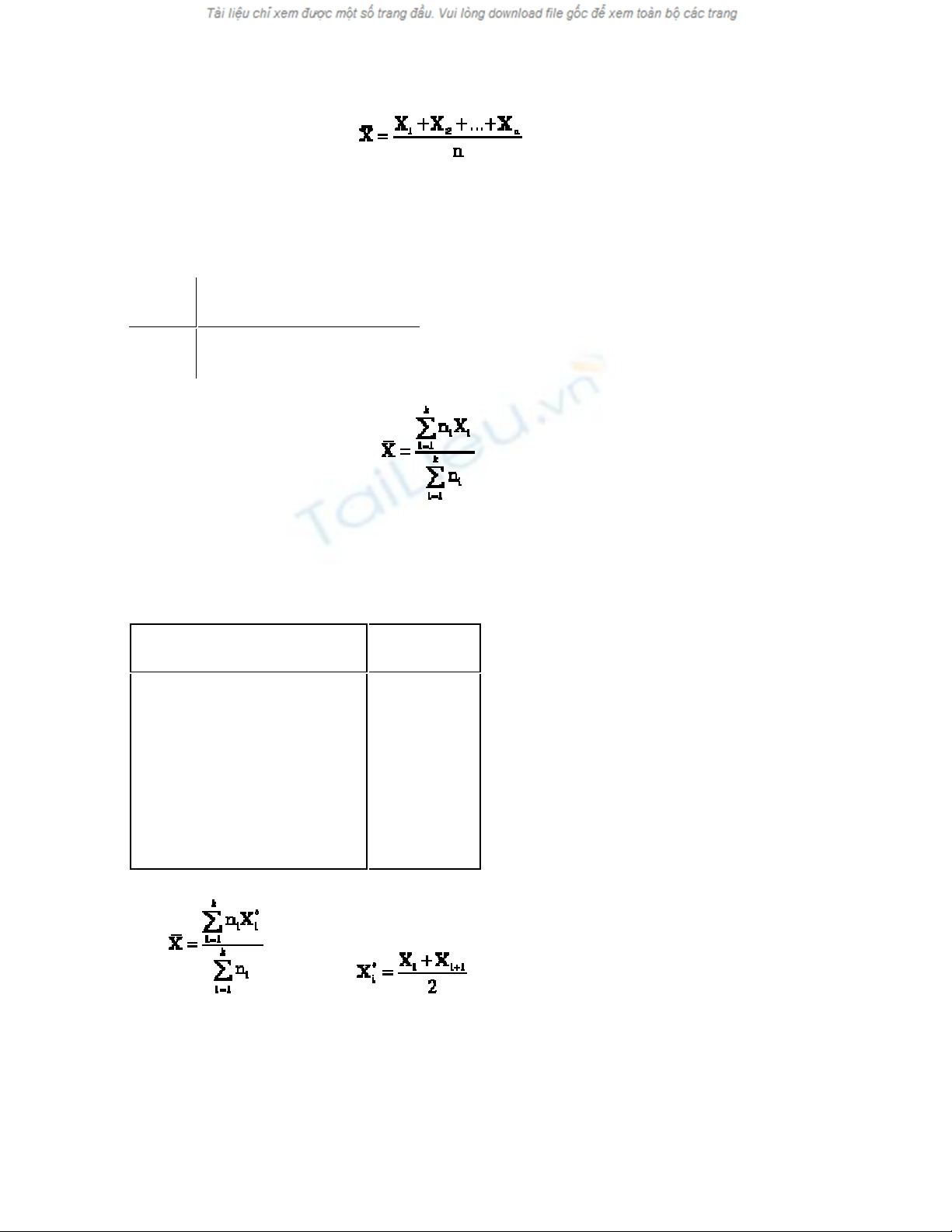
Định nghĩa 1.4. Ta gọi số là trung bình mẫu.
- Nếu mẫu cho dưới dạng
X X1 X2 .… Xk
ni n1 n2 …. nk
với n = n1 + n2 + … + nk thì
- Nếu mẫu cho dưới dạng khoảng
Khoảng Tần số ni
x1 – x2 n1
x2 – x3 n2
………. ………
xk – xk + 1 nk
thì trong đó .
Ø Phương sai mẫu
Định nghĩa 1.5. Phương sai mẫu là một số, ký hiệu được xác định bởi
Số được gọi là phương sai mẫu điều chỉnh.
Ví dụ 1.6. Cho mẫu quan sát đối với đại lượng ngẫu nhiên X là
Xi 1 2 3 4
ni 20 15 10 5
Tìm
Giải. Ta có
Từ đó,