1
1
CHƯƠNG VIII
TỰ TƯƠNG QUAN
–CHỌN MÔ HÌNH –
THẨM ĐỊNH VIỆC CHỌN MÔ HÌNH
2
8.1.1. Bảnchất và nguyên nhân củatựtương quan
Trong mô hình hồiquytuyến tính cổđiển chúng ta giả
định không có tương quan giữacácphầndưhay
Cov(uiuj) = 0 vớimọii, j.
⇒Cov(ui,uj) ≠0: tựtương quan
8.1. Tựtương quan (tương quan chuỗi)
t
ui
t
ui
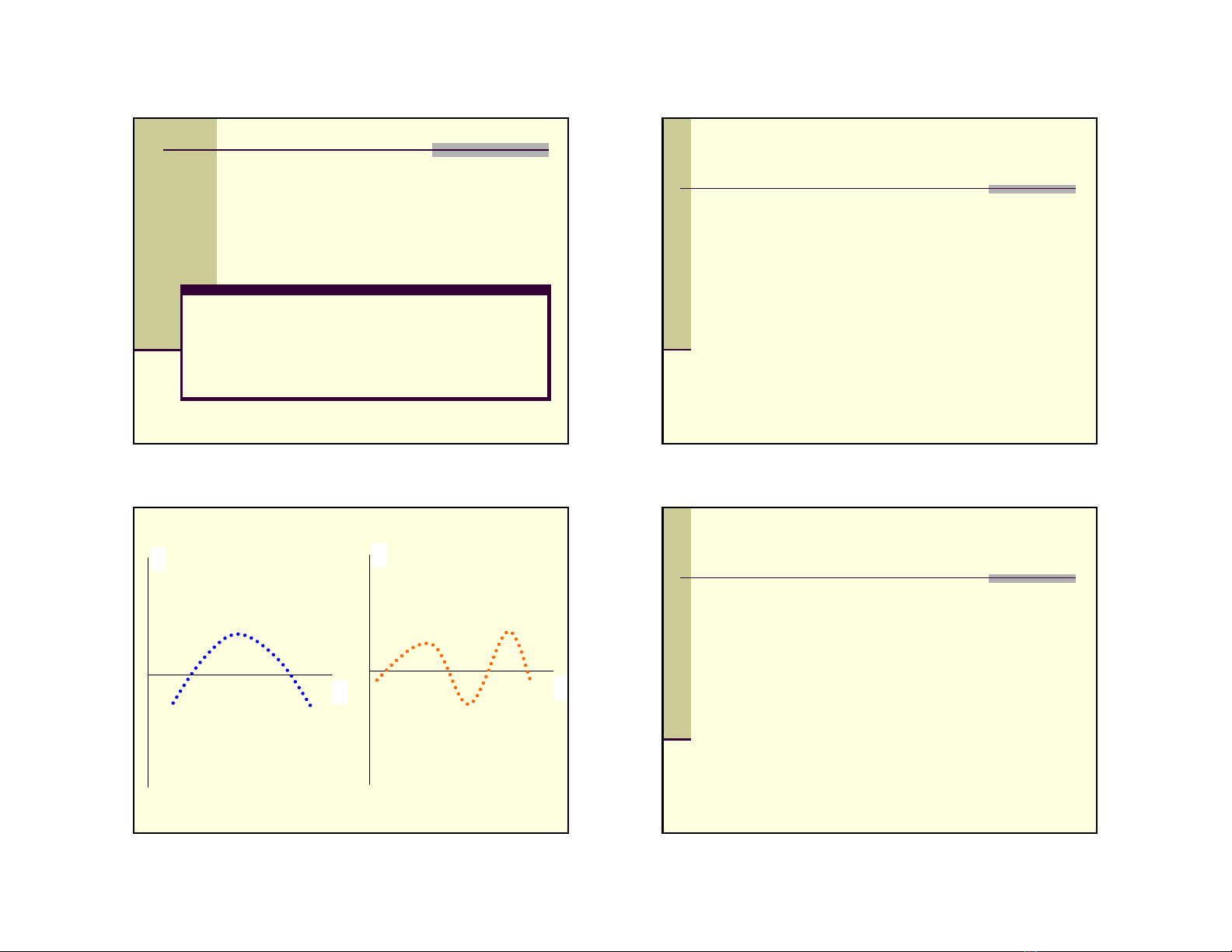
Cho thấycómộtxuhướng tuyến tính xãy ra ở2 mô hình trên
a) b)
4
•Chuỗi có tính chất quán tính theo chu kỳ
•Hiệntượng mạng nhện: dãy sốcung vềcafé nămnay
phụthuộcvàogiánămtrước=> u
ikhông còn ngẫu
nhiên nữa.
•Dãy sốcó tính chấttrễ: tiêu dùng ởthờikỳnày
chẳng những phụthuộcvàothunhậpkỳnày mà còn
phụthuộc vào tiêu dùng củakỳtrướcnữa.
* Nguyên nhân khách quan:
2
5
* Nguyên nhân chủquan
•Chọndạng mô hình sai (thường xảyraởmô hình
với chi phí biên)
•Đưathiếubiếngiải thích vào mô hình
•Việcxửlý sốliệu.(sốliệu tháng = sốliệu quý/3)
6
•Nếuvẫnápdụng OLS khi mô hình có hiệntượng tự
tương quan thì sẽcó các hậuquảsau:
•-Cácướclượng không chệch nhưng đó là không phải
là các hiệuquảvì đó không phảilàcácướclượng có
phương sai nhỏnhất.
•Phương sai củacácướclượng là các ướclượng chệch
vì vậycáckiểmđịnh t và F không còn hiệuquả.
•là ướclượng chệch củaδ2
•R2củamẫulàướclượng chệch (dưới) củaR
2tổng thể
•Các dựbáo vềY không chính xác
2
ˆ
δ
8.1.2. Hậuquảcủatựtương quan
7
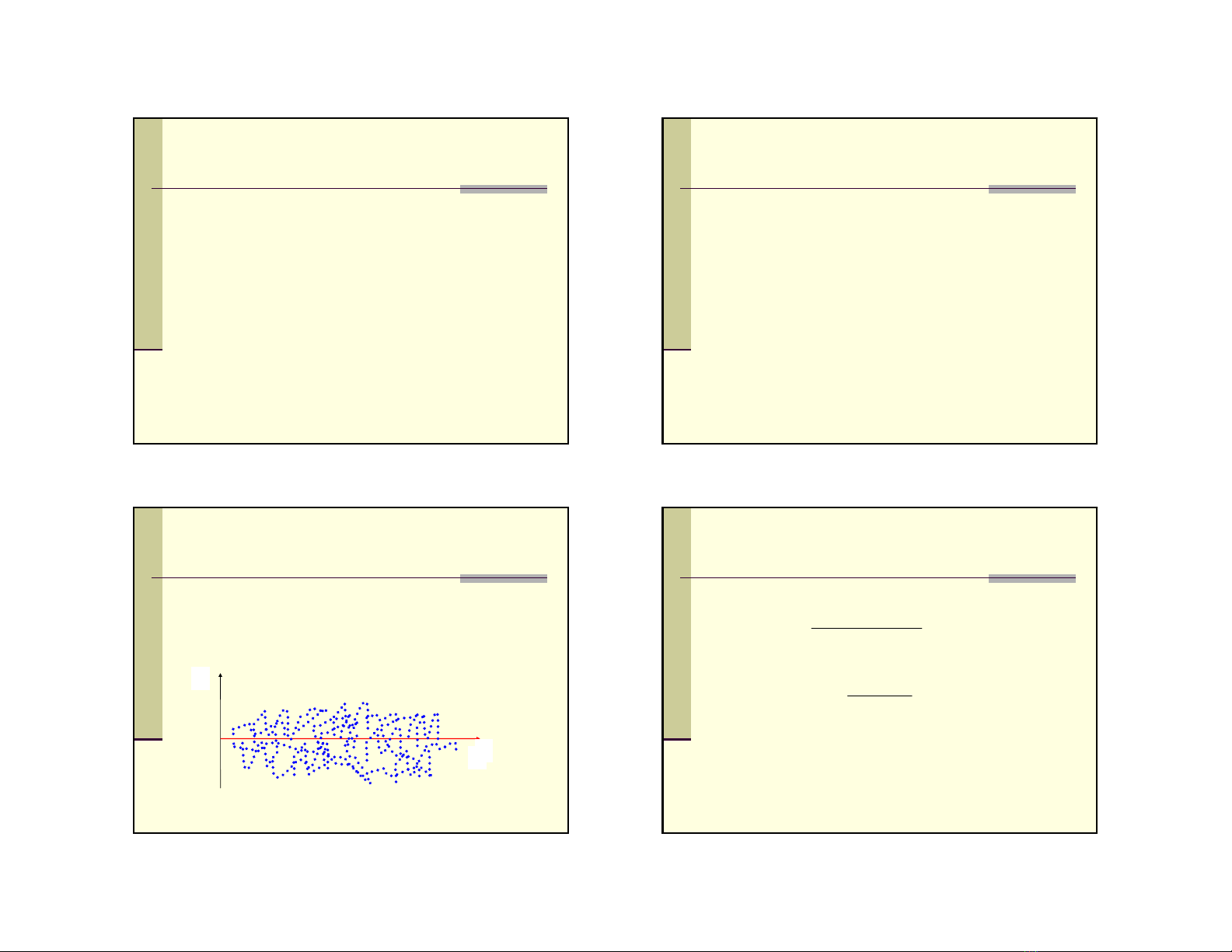
a. Đồ thị
Chúng ta có thểphát hiệnhiệntượng tựtương quan bằng
cách quan sát đồ thịphầndưcủamôhìnhtrêndữliệu
chuỗithờigian.
et
t
Phầndưphân bốmột cách ngẫu nhiên xung quanh giá trị
trung bình củanó.
8.1.3. Cách phát hiệntựtương quan
8
Thống kê d của Durbin – Watson đượcđịnh nghĩanhư
sau:
Khi n đủ lớnthì d ≈2(1-ρ)
trong đó:
do -1 ≤ρ≤1, nên khi:
ρ= -1 => d = 4: tựtương quan hoàn hảoâm
ρ= 0 => d = 2: không có tựtương quan
ρ= 1 => d = 0: tựtương quan hoàn hảodương
∑
∑
−
−
=2
2
1)(
i
ii
e
ee
d
∑
∑
−
=2
1
i
ii
e
ee
ρ
b. Dùng kiểmđịnh d của Durbin – Watson
3
9
dU< d < 4-dL
Không bác bỏKhông có tựtương quan âm
hoặcdương
4-dU ≤d ≤4-dL
Không quyết
định
Không có tựtương quan âm
4-dL< d < 4Bác bỏKhông có tựtương quan âm
dL≤d ≤dU
Không quyết
định
Không có tựtương quan
dương
0 < d < dL
Bác bỏKhông có tựtương quan
dương
NếuQuyếtđịnhGiảthiếtH
0
Trong đód
Uvà dLlà các giá trịtra bảng giá trịd.
b. Dùng kiểmđịnh d của Durbin – Watson (tt)
10
•Trong thựctếkhi tiếnhànhkiểmđịnh Durbin –
Watson, ngườitathường áp dụng quy tắckiểm
định đơngiảnsau:
•Nếu1 < d < 3 thì kếtluận mô hình không có tự
tương quan.
•Nếu0 < d < 1 thì kếtluậnmôhìnhcótựtương
quan dương.
•Nếu3 < d < 4 thì kếtluậnmôhìnhcótựtương
quan âm.
* Chú ý:
Nếud thuộc vùng chưa quyếtđịnh, chúng ta sẽ
sửdụng quy tắckiểmđịnh cảibiênnhưsau:
i) H0: ρ= 0; H1: ρ> 0. Nếud < dUthì bác bỏH0
và chấpnhậnH
1(vớimức ý nghĩaα), nghĩalà
có tựtương quan dương.
ii) H0: ρ= 0; H1: ρ< 0. Nếud > 4 - dUthì bác bỏ
H0và chấpnhậnH
1(vớimức ý nghĩaα), nghĩa
là có tựtương quan âm.
iii) H0: ρ= 0; H1: ρ≠0. Nếud <dUhoặcd > 4 -
dUthì bác bỏH0và chấpnhậnH
1(vớimứcý
nghĩa2α), nghĩalàcótựtương quan (âm hoặc
dương).
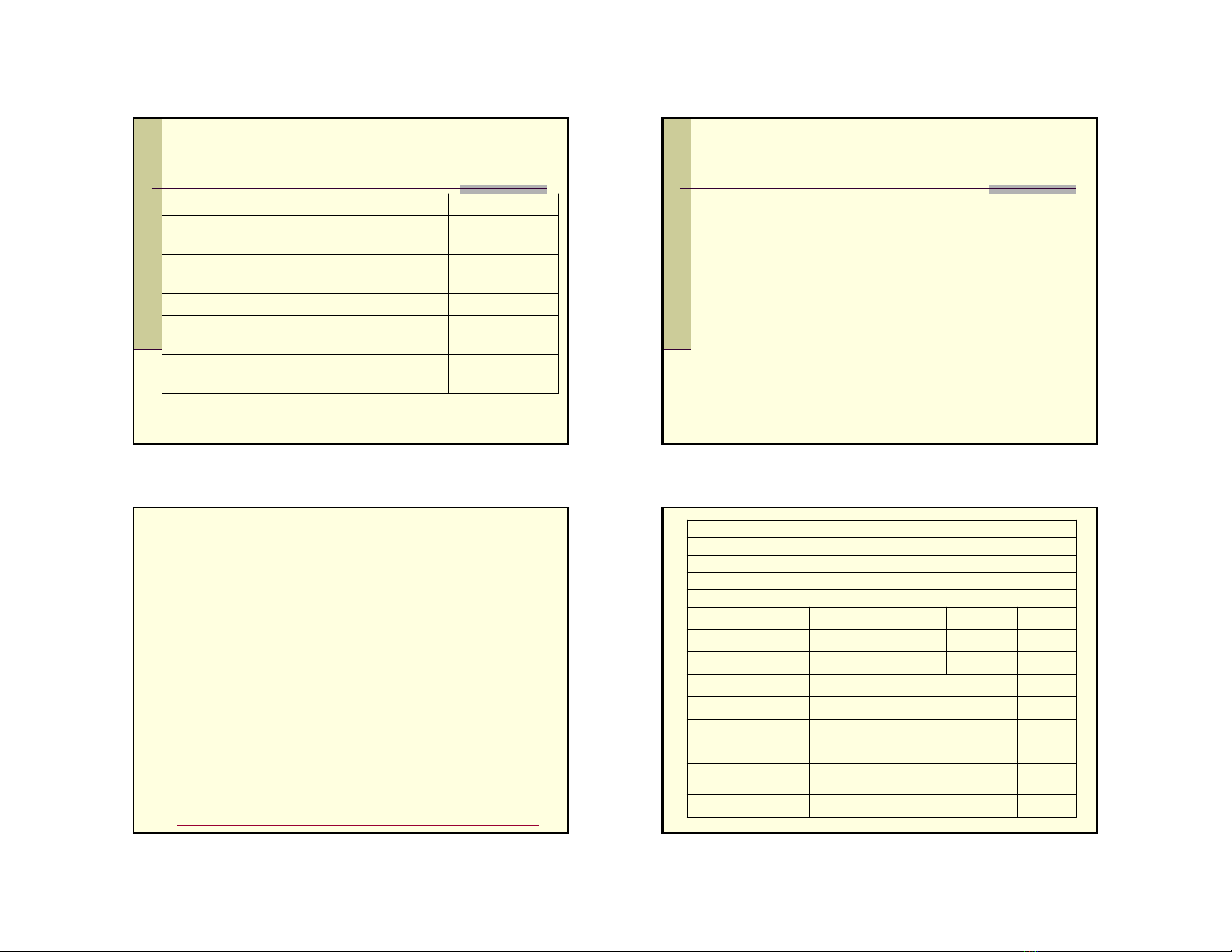
Bài tậpướclượng bằng phương pháp Durbin Watson
0.000000Prob(F-statistic)0.213684Durbin-Watson stat
1674.298F-statistic-97.12439Log likelihood
4.586754Schwarz criterion212.9500Sum squared resid
4.505654Akaike info criterion2.251719S.E. of regression
14.22579S.D. dependent var0.974946Adjusted R-squared
87.70000Mean dependent var
0.975529R-squared
0.000020.249681.46051529.57497C
0.000040.918180.017122
0.700589PRODUCT
Prob. t-StatisticStd. ErrorCoefficientVariable
Included observations: 44
Sample: 1959 2002
Date: 05/23/11 Time: 21:27
Method: Least Squares
Dependent Variable: RWAGES
4
13
Phân tích kếtquả
Kếtquảhồihồi qui cho thấycáchệsốhồiqui
củabiếntiềnlương thựctế(RWAGES) và
biếnnăng suấtlaođộng (PRODUCT) có ý
nghĩathống kê
R2= 0.975529 rấtlớn, nênmôhìnhrất phù
hợp
Nhưng do dựliệutrênlàdữliệuchuỗi, nên có
khảnăng xảyrahiệntượng tựtương quan.
Ta cầnkiểmđịnh hiệntượng này
-5
-4
-3
-2
-1
0
1
2
3
4
1940 1960 1980 2000 2020
NAM
RESID
Nhìn vào đồ thịchúng ta nhậnthấyphầndưphân bốcó vẻ
không ngẫu nhiên. Các phầndưnhậngiátrịâm sau đó
tăng dầnrồigiảmvànhậngiátrịâm trởlại
Nhìn vào đồ thị, ta nhậnthấycókhảnăng xảyra
tương quan dương giữae
ivà ei-1 khá rõ
-5
-4
-3
-2
-1
0
1
2
3
4
-5 -4 -3 -2 -1 0 1 2 3 4
ETTRE
ET
16
Từkếtquảhồi qui RWAGES theo PRODUCT
ta có giá trịthống kê Durbin-Watson d =
0.213684
Với n = 45, α= 5%, k’ = 1( do có 1 biếnđộc
lập). Tra bảng ta có đượcd
L= 1.475, du=
1.566
Do d = 0.213684 <d
L= 1.475 →bác bỏH0,
chấpnhậnH1. Tứclàcótương quan bậc
nhất trong các phầndư.
5
17
Xét mô hình:
Yt= β1+ β2Xt+ ut(8.1)
ut= ρ1ut-1 + ρ2ut-2 + … + ρput-p + vt
ta cầnkiểmđịnh giảthiếtH
0: ρ1= ρ2= … = ρρ= 0, có
nghĩa là không tồntạitựtương quan ởbấtkỳbậcnào
trong sốtừbậc1 đếnbậcp.
Bước1: Ướclượng (8.1) bằng OLS, tìm phầndưet
Bước2: Dùng OLS để ướclượng mô hình
et= β1+ β2Xt+ ρ1et-1 + ρ2et-2 + ..+ ρpet-p + εt
từđây ta thu đượcR
2.
c. Dùng kiểmđịnh Breusch – Godfrey (BG)
18
Bước3: vớin đủ lớn, (n-p)R2có phân phốixấpxỉ
χ2(p).
-Nếu (n-p)R2> χ2α(p): Bác bỏH0, nghĩalàcótự
tương quan ít nhấtởmộtbậcnàođó.
-Nếu (n-p)R2≤χ
2α(p): ChấpnhậnH
0, nghĩalà
không có tựtương quan.
-Lệnh : [equation] view/redual test/resdual
correlation LM test
c. Dùng kiểmđịnh Breusch – Godfrey (BG) (tt)
Bài tậpchương 8 : kiểmđịnh BG
0.000000Prob(F-statistic)0.683880Durbin-Watson stat
5978.979F-statistic-150.0818Log likelihood
9.904243Schwarz criterion29109.09Sum squared resid
9.811728Akaike info criterion31.68220S.E. of regression
448.3518S.D. dependent var0.995007Adjusted R-squared
1512.061Mean dependent var0.995173R-squared
0.0000-7.21704922.37920-161.5118C
0.000077.323860.0088480.684186THUNHAP
Prob. t-StatisticStd. ErrorCoefficientVariable
Included observations: 31
Sample: 1958 1988
Date: 05/27/11 Time: 14:32
Method: Least Squares
Dependent Variable: TIEUDUNG
0.001134Prob(F-statistic)1.895118Durbin-Watson stat
7.114283F-statistic-141.0533Log likelihood
9.543309Schwarz criterion16257.74Sum squared resid
9.358279Akaike info criterion24.53851S.E. of regression
31.14969S.D. dependent var0.379433Adjusted R-squared
-3.30E-13Mean dependent var0.441489R-squared
0.3437-0.9638960.193062-0.186092RESID(-2)
0.00044.0653900.1924230.782273RESID(-1)
0.9673-0.04141617.33445-0.717916C
0.94070.0750950.0068550.000515THUNHAP
Prob. t-StatisticStd. ErrorCoefficientVariable
Presample missing value lagged residuals set to zero.
Date: 05/27/11 Time: 14:35
Method: Least Squares
Dependent Variable: RESID
Test Equation:
0.001067Probability
13.68617Obs*R-squared
0.000385Probability10.67142F-statistic
Breusch-Godfrey Serial Correlation LM Test:
