337
MỘT SỐ PHƯƠNG PHÁP PHÂN TÍCH
TÍNH ỔN ĐỊNH CỦA PHƯƠNG TRÌNH VI PHÂN
Mai Quang Vinh1
1. Khoa Sư phạm, Trường Đại học Thủ Dầu Một
TÓM TẮT
Phương trình vi phân là một công cụ hiệu quả được sử dụng rộng rãi để mô hình các vấn đề
thực trong nghiên cứu khoa học kỹ thuật và đời sống. Một mô hình (gồm các phương trình vi phân)
thường bao gồm các tham số liên quan và điều kiện ban đầu của các đại lượng đang khảo sát. Một
câu hỏi rất tự nhiên là đầu ra của mô hình phụ thuộc như thế nào với đầu vào của mô hình? Vấn đề
này đã thu hút được nhiều sự quan tâm cho đến ngày nay. Trong khảo cứu này, chúng tôi sẽ giới
thiệu một số thành tựu đạt được trong nỗ lực trả lời câu hỏi trên. Cùng với đó là một số chủ đề nghiên
cứu liên quan có thể được triển khai trong thời gian tới.
Từ khóa: hàm Lyapunov, lý thuyết mạng phản ứng hóa học, Phương trình vi phân, tính ổn định.
1. TỔNG QUAN
Phương trình vi phân là một phương trình toán học phụ thuộc vào một biến độc lập duy nhất.
Nó biểu diễn mối quan hệ giữa một hàm (hoặc nhiều hàm) chưa được biết và đạo hàm của chúng. Lý
thuyết về phương trình vi phân đã được phát triển từ rất sớm và thu hút được nhiều sự quan tâm
nghiên cứu (Isaac Newton, 1744). Nhiều kết quả về phương trình vi phân đã được khám phá. Phương
trình vi phân đã được sử dụng rộng rãi để mô hình các hiện tượng trong nghiên cứu khoa học, kỹ
thuật, kinh tế và các lĩnh vực khác (George Simmons, 2016; Vladimir Kolmanovskii và nnk, 2013;
Edelstein-Keshet, 2005; Lee Segel và nnk, 2013). Sẽ rất khó để trình bày những ứng dụng phong phú
của phương trình vi phân. Do đó. ở đây chúng tôi chỉ tóm tắt một số ứng dụng phổ biến và cơ bản.
Trong nghiên cứu vật lý, phương trình vi phân thường được sử dụng để mô hình vấn đề đang
quan tâm. Chẳng hạn, mô hình sự chuyển động cả vật thể, sự chuyển động của dao động cưỡng bức.
Phương trình vi phân còn được xem là một công cụ hỗ trợ để tìm lời giải cho các mô hình gồm các
phương trình đạo hàm riêng (Farkhad Aliev và nnk, 2023; Venkataraman Balakrishnan, 2020).
Trong kinh tế, phương trình vi phân được sử dụng để mô hình sự tăng trưởng kinh tế, chu kỳ giao
dịch thương mại (Anastasios Tsoularis, 2021). Phương trình vi phân được sử dụng để phân tích các vấn
đề tối ưu hóa trong kinh tế, chẳng hạn như tìm kiếm chiến lược đầu tư hoặc tiêu dùng tối ưu. Những mô
hình này thường liên quan đến việc tối đa hóa các hàm lợi ích có ràng buộc (K. S. Bhamra, 2015).
Phương trình vi phân cũng được sử dụng rộng rãi để mô hình các vấn đề thực tế trong sinh học.
Chẳng hạn, mô hình sự tương tác giữa các loài trong một cộng đồng, mô hình sự phát triển của tế
bào, mô hình dịch bệnh. Bên cạnh đó, phương trình vi phân cũng được sử dụng rộng rãi trong nghiên
cứu cơ chế động học của enzyme (Edelstein-Keshet, 2005; Vinh Quang Mai và nnk, 2018; Vinh
Quang Mai và nnk, 2021). Ngoài ra, phương trình vi phân cũng được sử dụng rộng rãi trong nghiên
cứu hóa học. Có những lý thuyết toán học riêng biệt dành cho nghiên cứu các hệ phản ứng sinh hóa
phức tạp (Feinberg, 2019; Hirokazu Komatsu và nnk, 2018).
Có thể thấy ứng dụng phong phú của phương trình vi phân trong nghiên cứu các lĩnh vực khoa
học, kỹ thuật và đời sống. Khi sử dụng phương trình vi phân để mô hình, việc tìm nghiệm của nó là
cần thiết. Một khía cạnh thu hút được nhiều sự quan tâm trong khi sử dụng các mô hình phương trình
vi phân là tính ổn định của mô hình. Nói cách khác, nghiệm của mô hình sẽ phụ thuộc vào điều kiện
ban đầu của mô hình như thế nào? Nhiều nỗ lực đã được thực hiện để trả lời câu hỏi này (Seyed
338
Nikravesh, 2018; Marc Roussel, 2019). Trong báo cáo này, một số kết quả về phân tích tính ổn định
của phương trình vi phân sẽ được thảo luận.
Báo cáo sẽ được tổ chức như sau. Mục 2 sẽ trình bày sơ lược về phương pháp nghiên cứu được
sử dụng trong khảo cứu này. Các kết quả của khảo cứu này sẽ được trình bày trong mục 3. Cuối cùng,
một số nhận xét cũng như một vài hướng nghiên cứu liên quan sẽ được tóm tắt trong mục 4.
2. PHƯƠNG PHÁP NGHIÊN CỨU
Trong báo cáo này, chúng tôi sử dụng phương pháp nghiên cứu điển hình cho các nghiên cứu
toán học lý thuyết. Cụ thể, phương pháp tra cứu, phân tích, tổng hợp tài liệu đã được sử dụng ở đây.
Dưới đây là tóm lược về cơ sở toán học cần thiết cho nghiên cứu tiếp theo. Chi tiết hơn có thể được
tìm thấy trong (Isaac Newton, 1744). Xét (hệ) phương trình vi phân
𝑥󰇗=𝑓(𝑥),
(1)
trong đó x là một hàm số chưa biết của t và 𝑥󰇗 là đạo hàm cấp một của nó.
Định nghĩa 2.1. Trạng thái dừng của (hệ) phương trình vi phân (1) là nghiệm của (hệ)
phương trình f(x) = 0.
Định nghĩa 2.2. Trạng thái dừng 𝑥∗ của (1) là ổn định nếu với mọi ϵ > 0, tồn tại δ > 0
mà ||x(0) - x*|| < δ, thì
||𝑥(𝑡)−𝑥∗||<𝜖 với mọi 𝑡≥0.
Ngược lại, nó là không ổn định.
Trạng thái dừng của (1) được gọi là ổn định tiệm cận nếu nó ổn định và
𝑙𝑖𝑚 𝑡→∞𝑥(𝑡)=𝑥∗.
Định nghĩa 2.3. Miền hấp dẫn của (1) là tập tất cả các trạng thái của sao cho nghiệm
của (1) xuất phát từ đó sẽ hội tụ về trạng thái dừng 𝑥∗ khi t → ∞. Nếu miền hấp dẫn là toàn bộ không
gian trạng thái, thì 𝑥∗ được gọi là ổn định tiệm cận toàn cục.
3. KẾT QUẢ VÀ THẢO LUẬN
Hai phương pháp phân tích tính ổn định của phương trình vi phân được trình bày trong
mục này. Đầu tiên là tiêu chuẩn Routh-Hurwitz cho phân tích tính ổn định địa phương của
phương trình vi phân. Tiếp theo là phương pháp Lyapunov thứ hai được khảo sát. Cần chú ý
rằng đây chỉ là một vài trong các cách tiếp cận bài toán phân tích tính ổn định của phương
trình vi phân đã được thiết lập.
3.1. Tiêu chuẩn Routh-Hurwitz
Trong mục này, chúng tôi sẽ khảo cứu tiêu chuẩn Routh-Hurwitz cho phân tích tính ổn
định địa phương của phương trình vi phân. Các ý chính được trình bày ở đây, các chi tiết sẽ được
lược bỏ. Mặc dù đã được thiết lập hơn một thế kỷ, giá trị của nó vẫn còn nguyên vẹn. Người đọc
quan tâm có thể xem thêm ở các tài liệu (Edelstein-Keshet, 2005; Edward John Routh, 1877; Adolf
Hurwitz, 1895).
Sự thay đổi về số lượng của quần thể bao gồm k loài với các quần thể N1, N2, ..., Nk được
cho bởi sẽ được cho bởi k phương trình:
𝑑𝑁1
𝑑𝑡 =𝑓1(𝑁1,𝑁2,…,𝑁𝑘),
𝑑𝑁2
𝑑𝑡 =𝑓2(𝑁1,𝑁2,…,𝑁𝑘),
339
….
𝑑𝑁𝑘
𝑑𝑡 =𝑓𝑘(𝑁1,𝑁2,…,𝑁𝑘),
hay được viết dưới dạng vectơ như sau
𝑑𝑁
𝑑𝑡 =𝐹(𝑁),
(2)
với N = (N1, N2, ..., Nk), F = (f1, f2, ..., fk) trong đó mỗi hàm f1, f2, ..., fk có thể phụ thuộc vào tất cả hoặc
một số hàm N1, N2, ..., Nk.
Giả sử phương trình vi phân (2) có trạng thái dừng là𝑁∗=(𝑁1∗,𝑁2∗,…,𝑁𝑘∗), tức là
F(N∗) = 0. Để xác định trạng thái dừng có ổn định (địa phương) hay không thì sử dụng ma
trận Jacobi J của F(N) được xác định bởi
𝐽=𝜕𝐹
𝜕𝑁(𝑁∗)=
(
𝜕𝑓1
𝜕𝑁1⋯𝜕𝑓1
𝜕𝑁𝑘
⋮ ⋱ ⋮
𝜕𝑓𝑘
𝜕𝑁1⋯𝜕𝑓𝑘
𝜕𝑁𝑘
)
(𝑁∗).
Đây là một ma trận hằng số.
Giả sử λ1, λ2, ..., λk là tất cả các giá trị riêng của phương trình đặc trưng det(J -λIk) = 0
hay
𝜆𝑘+𝑎1𝜆𝑘−1+𝑎2𝜆𝑘−2+⋯+𝑎𝑘=0.
(3)
Nếu tất cả các giá trị riêng có phần thực âm thì trạng thái dừng đang xét 𝑁∗ là ổn định
(địa phương). Do đó, tính ổn định của một điểm dừng có thể được xác định bằng cách tìm
tất cả các giá trị riêng λi, i = 1, 2, ..., k, của (3). Nói chung, đây là một việc không dễ dàng và
không phải lúc nào cũng có thể thực hiện được. May mắn thay, một tiêu chuẩn đơn giản hơn đã
được thiết lập bởi Edward John Routh và Adolf Hurwitz; xem trang 233 ở (Edelstein-Keshet,
2005). Dưới đây là nội dung của tiêu chuẩn.
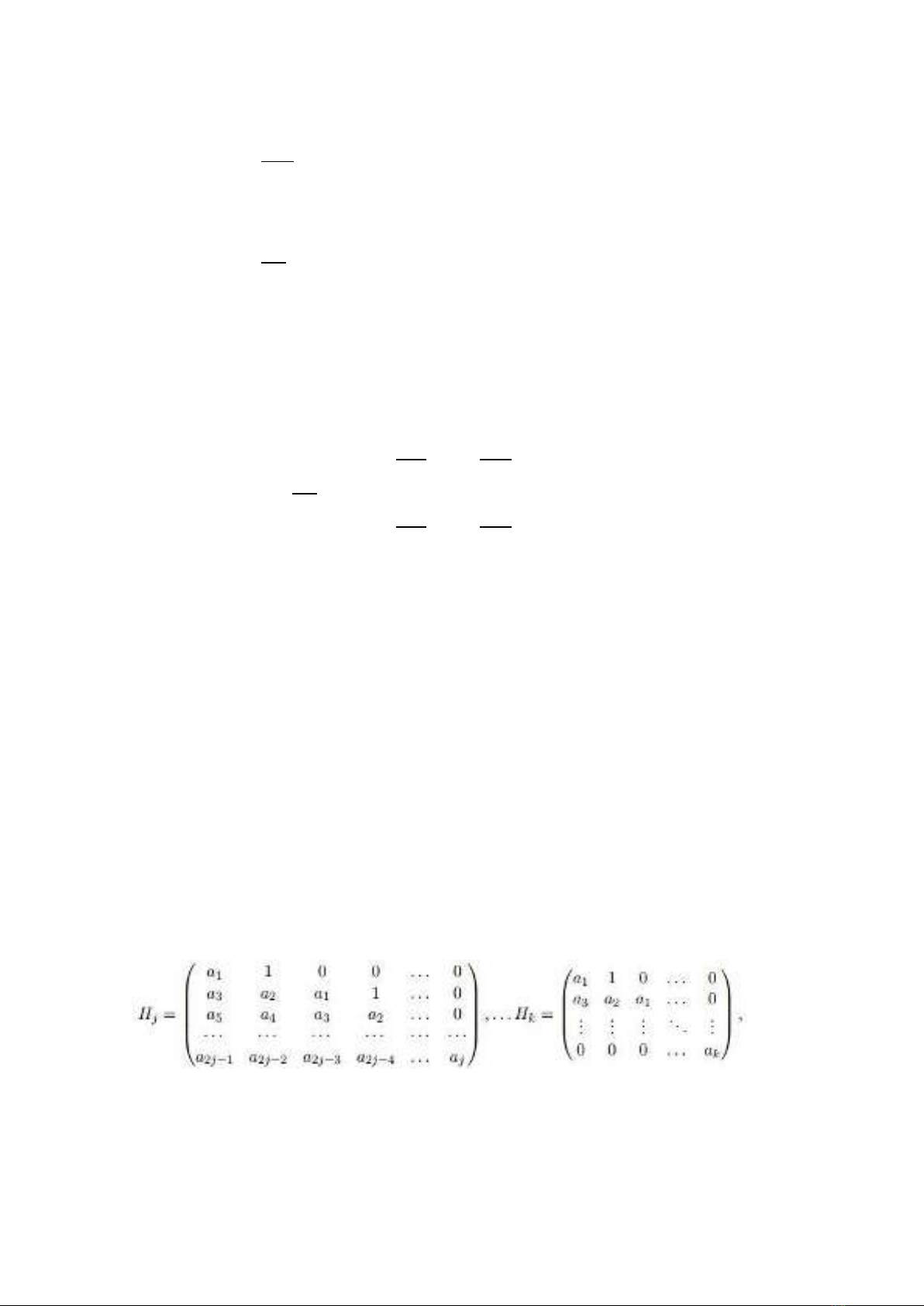
Định lý 3.1. Với phương trình đặc trưng (3), xét các ma trận được xác định như sau:
𝐻1=(𝑎1),𝐻2=[𝑎11
𝑎3𝑎2],𝐻3=[𝑎11 0
𝑎3𝑎2𝑎1
𝑎5𝑎4𝑎3],…
trong đó phần tử (l, m) trong ma trận Hj được cho bởi
𝑎𝑙𝑚 ={𝑎2𝑙−𝑚, 𝑘ℎ𝑖 0<2𝑙−𝑚<𝑘,
1, 𝑘ℎ𝑖 2𝑙=𝑚,
0, 𝑘ℎ𝑖 2𝑙<𝑚 ℎ𝑎𝑦 2𝑙>𝑘+𝑚.
340
Khi đó, tất cả các giá trị riêng có phần thực âm (hay 𝑁∗ là ổn định) nếu và chỉ nếu định
thức của tất cả các ma trận Hurwitz Hj đều dương, tức là
det𝐻𝑗>0, 𝑗=1,2,…,𝑘.
Dưới đây là tiêu chuẩn Routh-Hurwitz được triển khai cho các trường hợp k = 2, 3, 4 (Robert
May và nnk, 2007)
𝑘=2:
𝑎1>0,
𝑎2>0,
𝑘=3:
𝑎1>0,
𝑎3>0,
𝑎1𝑎2>𝑎3,
𝑘=4:
𝑎1>0,
𝑎3>0,
𝑎4>0,
𝑎1𝑎2𝑎3>𝑎3
2+𝑎1
2𝑎4.
Ví dụ 3.2. Giả sử x là động vật ăn thịt, y và z là con mồi của nó. Biết z tăng trưởng một cách
logistic khi không có kẻ săn mồi, x chết khi không có con mồi và y phát triển theo hàm mũ khi không
có kẻ săn mồi. Chúng ta sẽ sử dụng kỹ thuật Routh-Hurwitz để khám phá xem liệu những loài này có
thể cùng tồn tại ở trạng thái cân bằng ổn định hay không. Với các giả thiết, một mô hình toán học mô
tả sự phát triển của quần thể gồm ba loài như sau:
𝑑𝑥
𝑑𝑡=𝛼𝑥𝑧+𝛽𝑥𝑦−𝛾𝑥,
𝑑𝑦
𝑑𝑡=𝛿𝑦−𝜖𝑥𝑦,
𝑑𝑧
𝑑𝑡=𝜇𝑧(𝜁−𝑧)−𝜅𝑥𝑧 ,
trong đó α, β, γ, δ, ϵ, µ, ζ, κ là các hằng số dương. Giải hệ phương trình
dx/dt =dy/dt = dz/dt =0
thu được một trạng thái dừng không tầm thường của mô hình là
𝑥∗=𝛿
𝜖, 𝑦∗=𝛾−𝛼𝑧∗
𝛽, 𝑧∗=𝜁−𝜅
𝜇𝑥∗.
Trạng thái dừng này có ý nghĩa về mặt sinh học khi γ > αz∗ và ζ > κx∗/µ. Tiếp theo, ta tính được ma
trận Jacobi của mô hình được cho bởi
𝐽=[𝛼𝑧∗+𝛽𝑦∗−𝛾 𝛽𝑥∗𝛼𝑥∗
−𝜖𝑦∗𝛿−𝜖𝑥∗0
−𝜅𝑧∗0𝜇𝜁−2𝜇𝑧∗−𝜅𝑥∗]
hay
𝐽=[ 0 𝛽𝑥∗𝛼𝑥∗
−𝜖𝑦∗0 0
−𝜅𝑧∗0 −𝜇𝑧∗].
Khi đó, phương trình đặc trưng của ma trận Jacobi J là
λ3 + a1λ2 + a2λ + a3 = 0,
trong đó
𝑎1=𝜇𝑧∗,
𝑎2=𝜖𝛽𝑥∗𝑦∗+𝜅𝛼𝑥∗𝑧∗,
341
𝑎3=𝜇𝜖𝛽𝑥∗𝑦∗𝑧∗.
Kiểm tra trực tiếp, ta nhận thấy
𝑎1>0,
𝑎2>0,
𝑎1𝑎2>𝑎3.
Suy ra trạng thái dừng của hệ thỏa mãn tiêu chuẩn Routh-Hurwitz trong trường hợp k = 3.
Ta kết luận rằng trạng thái dừng này là ổn định.
Nội dung về tiêu chuẩn Routh-Hurwitz cho phân tích tính ổn định (địa phương) của phương
trình vi phân tạm dừng ở đây. Tiếp theo là một số thảo luận về phương pháp phân tích tính
ổn định của phương trình vi phân dựa theo hàm Lyapunov (hay phương pháp Lyapunov thứ
hai).
3.2. Phương pháp Lyapunov thứ hai
Bên cạnh cách tiếp cận địa phương như phương pháp Routh-Hurwitz được trình bày ở
trên, phương pháp Lyapunov thứ hai là một phương pháp nổi tiếng và thu hút được nhiều sự
quan tâm, cũng như đã đạt được nhiều kết quả độc đáo. Hai tài liệu sau giới thiệu kiến thức nhập môn
cũng như tổng hợp nhiều tiến bộ trong lĩnh vực này (Seyed Nikravesh, 2018; Marc Roussel, 2019).
Phương pháp Lyapunov dựa trên một ý tưởng đơn giản. Giả sử rằng V(x) là một hàm của
các biến trạng thái có cực tiểu tại điểm cân bằng và không có cực tiểu nào khác (paraboloid
là một ví dụ). Bây giờ, giả sử rằng chúng ta có thể chỉ ra rằng động lực học của hệ thống
dẫn đến sự giảm đều đặn của V trong một vùng lân cận (có thể lớn) nào đó của điểm cân
bằng. Điều này có nghĩa là chúng ta đang hướng tới cực tiểu của V, đây chính là điểm cân
bằng. Sau khi chỉ ra điều này, chúng ta có thể kết luận rằng điểm cân bằng ổn định trên toàn
bộ vùng lân cận của x∗ mà V giảm. Hàm V có các tính chất này được gọi là hàm Lyapunov
(Marc Roussel, 2019). Ý tưởng này có thể được cụ thể hóa như sau:
Định nghĩa 3.3. Gọi U là vùng không gian pha chứa điểm cân bằng x∗. Cho V: U → R là một
hàm liên tục và khả vi. Hàm V là hàm xác định dương đối với điểm x∗ nếu nó thỏa mãn hai điều kiện
sau:
V (0) = 0 và V (x) > 0 với mọi x ∈ U \ {0}.
Hàm V được gọi là hàm Lyapunov cho (1) tại x∗.
Định lý 3.4. Cho x∗ = 0 là một điểm cân bằng của (1) và V là một hàm xác định dương cho
điểm này. Điểm cân bằng x∗ là ổn định tiệm cận (các nghiệm hướng tới điểm này đối với các điều
kiện ban đầu trong lân cận U của x∗ nếu
𝑉󰇗(𝑥)=𝑑𝑉(𝑥)
𝑑𝑡 <0
với mọi x ∈ U \{x∗}.
Có thể thấy định lý này là một kết quả rất đẹp và độc đáo. Để sử dụng định lý này,
chúng ta phải thiết lập được hàm Lyapunov. Thật không may, thường rất khó để đưa ra hàm
Lyapunov cho một hệ cụ thể, ngoại trừ trong một số trường hợp đặc biệt khi tính chất của
bài toán gợi ý một lựa chọn cụ thể. Chứng minh của định lý này có thể được tìm thấy trong
(Hassan Khalil, 2002). Tiếp theo là một số ví dụ minh họa cho việc sử dụng định lý này.
Ví dụ 3.5. Xét hệ phương trình vi phân
𝑥󰇗=𝑦,