NGÂN HÀNG Đ KI M TRA- TOÁN 11- CH NG TRÌNH CHU NỀ Ể ƯƠ Ẩ
STT
Mã
câu
h iỏ
Ý,
th i ờ
gian
N i dungộĐiể
m
1 0401
15' Tính các gi i h n sau:ớ ạ 2,5
1A a,
3
3
3 2 5
lim 1 2
n n
n
+ +
+
1,0
2B b,
5 2.3
lim 4 3.5
n n
n n
+
−
1,5
1A a,
32 3
3
3
2 5
3
3 2 5 3
lim lim .
1
1 2 2
2
n n n n
n
n
+ +
+ + = =
++
1,0
2B b, Ta có:
3
1 2.
5 2.3 1
5
lim lim .
4 3.5 3
43
5
n
n n
nn n
+
+
= = −
− −
1,5
2 0401
15' Tính các gi i h n sau: ớ ạ 2,5
1A a,
2
3 2
lim 1
n n
n n
− + +
− +
1,0
2B b,
1 1
( 2) 3
lim ( 2) 3
n n
n n+ +
− +
− +
1,5
1A
3 2
2
2
3 1 2
3 2
lim lim 0.
1 1
11
n n n n n
n n
n n
− + +
− + + = =
− + − +
1,0
2B Ta có:
1,5
3 0401
B,10' Tính t ng ổ
( )
1
3 3 3 3 3( 1)
... ...
2 4
2 2 2 2
n
n
S
+
−
= − + − + + +
2,0
Đây là c p s nhân lùi vô h n có ấ ố ạ
1
1 3
,
2 2
q u= − =
. Do đó:
( )
1
3
3 3 3 3 3( 1) 3
2
... ... .
1
2 4
2 2 2 1 2
212
n
n
S
+
−
= − + − + + + = = +
+
1,0
1,0
4 0402
A,10' Tính gi i h n :ớ ạ
2
2
1
1
lim 3 2
x
x
x x
→−
−
+ +
2,0
Ta có
2
2
1 1 1
1 ( 1)( 1) 1
lim lim lim 2.
3 2 ( 1)( 2) 2
x x x
x x x x
x x x x x
→− →− →−
− + − −
= = = −
+ + + + +
1,0
1,0
5 0402
B,10' Tính gi i h n: ớ ạ
2
1
2 3
lim 1
x
x
x
→
− +
−
2,0
Ta có:
22
1 1
1
1
2 3 4 ( 3)
lim lim
1( 1)(2 3)
( 1)
lim ( 1)( 1)(2 3)
1 1
lim .
8
( 1)(2 3)
x x
x
x
x x
xx x
x
x x x
x x
→ →
→
→
− + − +
= =
−− + +
− − =
− + + +
−= −
+ + +
1,0
0,5
0,5
6 0402
B,10' Tính gi i h n: ớ ạ
3 2
4 2
3
5 3 9
lim 8 9
x
x x x
x x
→
− + +
− −
2,0
Ta có:
3 2 2
4 2 2 2
3 3
2
3
5 3 9 ( 3) ( 1)
lim lim
8 9 ( 1)( 9)
( 3)( 1)
lim 0
( 1)( 3)
x x
x
x x x x x
x x x x
x x
x x
→ →
→
− + + − +
= =
− − + −
− + =
+ +
1,0
1,0
7 0402
C,10' Tính gi i h n: ớ ạ
3
2
4 2
lim 2
x
x
x
→
−
−
3,0
Ta có:
( )
( )
( ) ( )
( )
2
3 3 3
3
2
2 2 3 3
2 2
2 2
3 3 3 3
2
23 3
( 4 2) 4 2 4 4
4 2
lim lim
2( 2) 4 2 4 4
4 8 4( 2)
lim lim
( 2) 4 2 4 4 ( 2) 4 2 4 4
4 1
lim .
3
4 2 4 4
x x
x x
x
x x x
x
xx x x
x x
x x x x x x
x x
→ →
→ →
→
− + +
−
=
−
− + +
− −
= =
− + + − + +
= =
+ +
1,0
1,0
1,0
8 0403
B,10'
Xét tính liên t c c a hàm s sau:ụ ủ ố
2
1Õu 1
( ) ¹i 1.
1
2Õu 1
xn x
f x t x
x
n x
−≠ −
= = −
+
− = −
2,0
TXĐ D=R ch a x=-1. Ta có: f(-1)=2 vàứ
2
1 1 1 1
1 ( 1)( 1)
lim ( ) lim lim lim ( 1) 2 ( 1)
1 1
x x x x
x x x
f x x f
x x
→− →− →− →−
− − +
= = = − = − = −
+ +
Do đó, hàm s liên t c t i x=-1.ố ụ ạ
1,0
1,0
9 0403
B,15'
Tìm giá tr m đ hàm s sau liên t c t i x=-1:ị ể ố ụ ạ
3 4 1 Õu 1
( ) .
1
Õu 1
xn x
f x x
m n x
+ − ≠ −
=+
= −
3,0
Ta có:
1 1 1
1
3 4 1 3 4 1
lim ( ) lim lim
1( 1)( 3 4 1)
3 3
lim 2
3 4 1
x x x
x
x x
f x xx x
x
→− →− →−
→−
+ − + −
= =
++ + +
= =
+ +
f(-1)=m. V y đ hàm s liên t c t i x=-1 khi và ch khi m=3/2.ậ ể ố ụ ạ ỉ
1,0
1,0
1,0
10 0402
B,15'
Ch ng minh ph ng trình sau có ít nh t m t nghi m thu c kho ngứ ươ ấ ộ ệ ộ ả
(-2;1):
5 3
2 5 1 0.x x− − =
3,0
Đ t f(x)=ặ
5 3
2 5 1x x− −
, ta có:
f(-1)=2, f(0)=-1
do đó f(-1).f(0)<0 (1)
f(x) liên t c trên R nên nó liên t c trên [-1;0] (2)ụ ụ
t (1) và (2) ph ng trình f(x)=0 có ít nh t m t nghi m trên kho ng ừ ươ ấ ộ ệ ả
(-1;0) t c là thu c kho ng (-2;1). ứ ộ ả
1,0
1,0
1,0
11 0502
A,15' Tính đ o hàm c a hàm s : ạ ủ ố
(2 1)(4 3)y x x= + −
.2,0
Ta có:
' (2 1)'(4 3) (2 1)(4 3)'
1 2 8 1
(4 3) (2 1) .
y x x x x
x
x x
x x x
= + − + + −
−
= − + + =
1,0
1,0
12 0502
A,15' Tính đ o hàm c a hàm s : ạ ủ ố
3 4.
4 5
x
yx
−
=+
2,0
Ta có:
2
2 2
(3 4)'(4 5) (3 4)(4 5)'
'(4 5)
3(4 5) (3 4)4 31 .
(4 5) (4 5)
x x x x
yx
x x
x x
− + − − +
=+
+ − −
= =
+ +
1,0
1,0
13 0503
B,15' Tính đ o hàm c a hàm s : ạ ủ ố
2
1 os 2
x
y c= +
3,0
Ta có:
'
2
2
2
2 2
1
' 1 os 2
2 1 os 2
1.2 os (cos )'
2 2
2 1 os 2
1 sinx
.2 os ( sin ).( )' .
2 2 2
2 1 os 4 1 os
2 2
x
y c
x
c
x x
c
x
c
x x x
c
x x
c c
= + =
+
+
−
= − =
+ +
1,0
1,0
1,0
14 0501
B,15' Cho đ ng cong (C):ườ
3
( ) .y f x x
= =
Vi t ph ng trình ti p tuy n c aế ươ ế ế ủ
(C), bi t ti p tuy n đó song song v i đ ng th ng y=-x.ế ế ế ớ ườ ẳ
3,0
Vì ti p tuy n c a (C) song song v i đ ng th ng y=-x nên có h sế ế ủ ớ ườ ẳ ệ ố
góc k=-1.
1,0
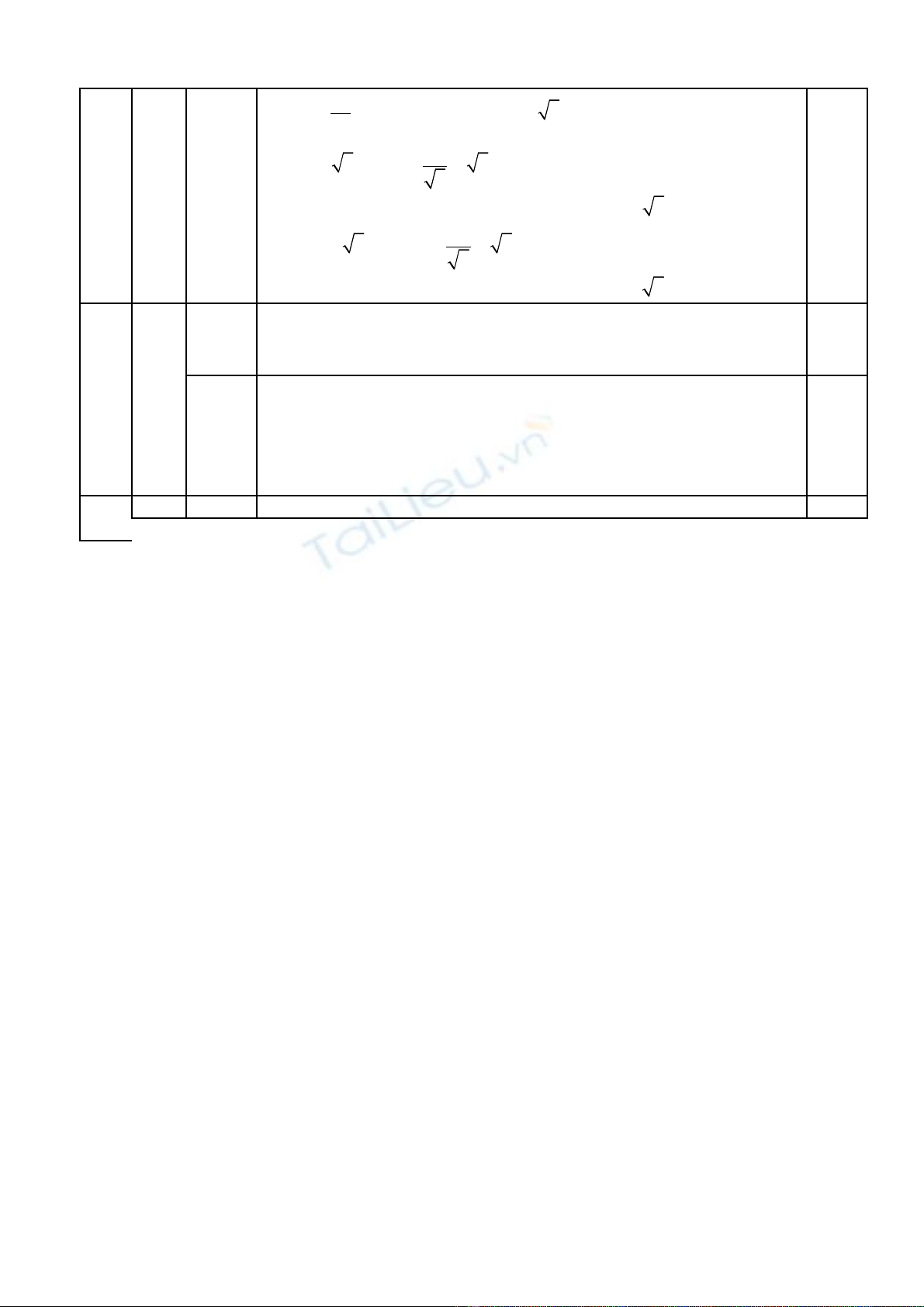
Do đó
2
0 0
2
0
31 3 3x x
x
− = − ⇔ = ⇔ = ±
khi
0 0 0
3
3×3µ' 1
3
x th y v y= = = = −
ph ng trình ti p tuy n t ng ng là: ươ ế ế ươ ứ
2 3y x= − +
khi
0 0 0
3
3×3µ' 1
3
x th y v y= − = − = = −
ph ng trình ti p tuy n t ng ng là: ươ ế ế ươ ứ
2 3.y x= − −
1,0
1,0
15 0501
C,10'
Cho đ ng cong (C):ườ
2
( ) 2 3.y f x x x= = − +
Vi t ph ng trình ti pế ươ ế
tuy n c a (C), bi t ti p tuy n đó vuông góc v i đ ng th ngế ủ ế ế ế ớ ườ ẳ
x+4y=0.
3,0
Vì ti p tuy n c a (C) vuông góc v i đ ng th ng x+4y=0 nên có hế ế ủ ớ ườ ẳ ệ
s góc k=4ố
Do đó
0 0
2 2 4 3x x− = ⇔ =
khi
0 0
3×6x th y= =
ph ng trình ti p tuy n c a (C) là: y=4x-6.ươ ế ế ủ
1,0
1,0
1,0
16 0301
A,10’ Cho t diên ABCD.ư
Ch ng minh: ư
AB CD AD CB+ = +
uuur uuur uuur uuur
1,5
Biên đôi vê trai:
AB CD AD DB CB BD+ = + + +
uuur uuur uuur uuuur uuur uuuur
( )AB CD AD CB DB BD+ = + + +
uuur uuur uuur uuur uuuur uuuur
AB CD AD CB+ = +
uuur uuur uuur uuur
0,5
0,5
0,5
17 0303
15’ Cho hình chóp S.ABCD co SA
⊥
(ABCD), đay ABCD la hinh
vuông. Goi M, N lân l t la trung điêm cua canh SB va SD. ươ 2,0
1B Ch ng minhư
( )BC SAB⊥
2C Ch ng minhMN ư
⊥
(SAC)
1B
Ch ng minh ư
( )BC SAB⊥
( )
BC AB
BC SAB
BC SA
⊥⇒ ⊥
⊥
1
2C
Ch ng minh MN ư
⊥
(SAC)
( )
BD SA
BD SAC
BD AC
⊥⇒ ⊥
⊥
(1)
MN // BD (2)
T (1) va (2) suy ra MN ư
⊥
(SAC)
1
18
0302
B, 10’
Cho t diên ABCD v i ư ơ
( )AB BCD⊥
va AB = a; đay BCD la tam
giac đêu canh 2a. Goi H la trung điêm cua canh CD. Tim goc tao b i ơ
HA
uuur
va
BH
uuur
1,5
Goc tao b i ơ
HA
uuur
va
BH
uuur
Tinh BH = a
3
· ·
0
3
tan 30
3
3
a
AHB AHB
a
= = ⇒ =
(
HA
uuur
;
BH
uuur
) = 1800 – 300 = 1500
0,5
0,5
0,5
19
0302
15’ Cho t di n đ u ABCD có c nh b ng a. Hãy tính các tích vô h ngứ ệ ề ạ ằ ướ
sau:
2,0
1A
.AB AD
uuur uuur
0,75
2C
.AB CM
uuur uuuur
trong đó M là trung đi m BD.ể1,25
1A
2
0 2
. . .cos( . )
1
. .cos 60 2 2
AB AD AB AD AB AD
a
a a a
=
= = =
uuur uuur uuur uuur uuur uuur
0,25
0,5
2C
0 0 2 2
2 2 2
. ( ) . .
3 3 3 1
. cos 30 . .cos 60 . . .
2 2 2 2
3
4 2 4
AB CM AB AM AC AB AM AB AC
a a a a a a
a a a
= − = −
= − = −
= − =
uuur uuuur uuur uuuur uuur uuur uuuur uuur uuur
0,5
0,5
0
A
A
B
B
C
C
D
B
D
H
2a
a
C
A
A
C
C
D
D
B
B
A
A
M
S
B
C
D
A
M
N
I
K