131
NGHIÊN CỨU TÍCH CHẬP VÀ ỨNG DỤNG TÍCH
CHẬP TRONG THỰC TẾ
Võ Đnh Chân, Nguyễn Anh Được, Nguyễn Ngọc Thiện*
*Viện Kỹ thuật HUTECH, Trường Đại học Công nghệ TP. Hồ Chí Minh
GVHD: ThS. Trần Duy Cường
TÓM TẮT
Trong toán học và đặc biệt là trong giải tích, tích chập là 1 phép toán thực hiện đối với 2 hàm số f và g, kết quả
cho ra một hàm số thứ 3. Phép tích chập khác với tương quan chéo ở chỗ nó cần lật kernel theo chiều ngang và
dọc trước khi tính tích.
Từ khóa: giải tích, tích chập, hàm số f, tương quan chéo, kernel
1. GIỚI THIỆU
Công thức của tích chập được định nghĩa như sau:
(f*g)(t) = ∫𝑓(𝜏).𝑔(𝑡−𝜏)𝑑𝜏
+∞
−∞
trong đó, mình sẽ định nghĩa các hàm tương ứng với bên học máy để dễ liên hệ về sau:
• f(t) là tín hiệu đầu vào
• g(t) là đáp ứng xung
• t là vị trí tương đối (độ trễ - t thường được dùng cho thời gian)
2. PHÂN TÍCH VÀ CÁCH TÍNH PHÉP TOÁN TÍCH CHẬP
Tích chập của 2 tính hiệu tuần hoàn: x(t) và h(t) sẽ tạo ra một tính hiệu mới Y(t):
Y(t) =x(t)*h(t) (1)
Và được định nghĩa:
Y(t)=
( ) ( )x h t d
−
−
(2)
Bằng cách thây đổi biến:
-
=>
=t-
ta nhận thấy,tích chập có tính giao hoán,tức là:
132
Y(t)=
( ) ( )h x t d
−
−
(3)
Tương tự,tích chập có tính kết hợp và phân phối:
[x(t) * h(t) * w(t)= x(t) * [h(t) * w(t)] (4)
x(t) * [ℎ1(t)+ℎ2(t)] = [x(t)*ℎ1(t)] + [x(t) *ℎ2(t)] (5)
Từ công thức (2) ,có thể thực hiện tích chập qua 4 bước sau:
-B1: tín hiệu
()h
được lấy ảnh gương và dịch theo thời gian để tạo thành tính hiệu
()ht
−
là một hàm theo
với tham số t
-B2: các tính hiệu
()x
và
được nhân lại với nhau cho với mọi giá trị của
với t được cố định tại
một vài vị trí
-B3: hàm tích
()x
*
()ht
−
được lấy tích với mọi
để tạo một giá trị y(t).
-B4: lặp lại các bước B1,B2,B3 khi t được thây đổi liên tục từ -
đến +
để tạo hàm y(t)
VD: Hình ảnh minh họa tích chập
1. Thể hiện mỗi hàm bằng một biến giả 𝜏.
2. Lấy đối xứng hàm qua trục tung: g(𝜏)→g(-𝜏)
3. Thêm biến thời gian t cho phép g(t-𝜏) trượt trên trục 𝜏
4. Bắt đầu t từ -∞ đến +∞
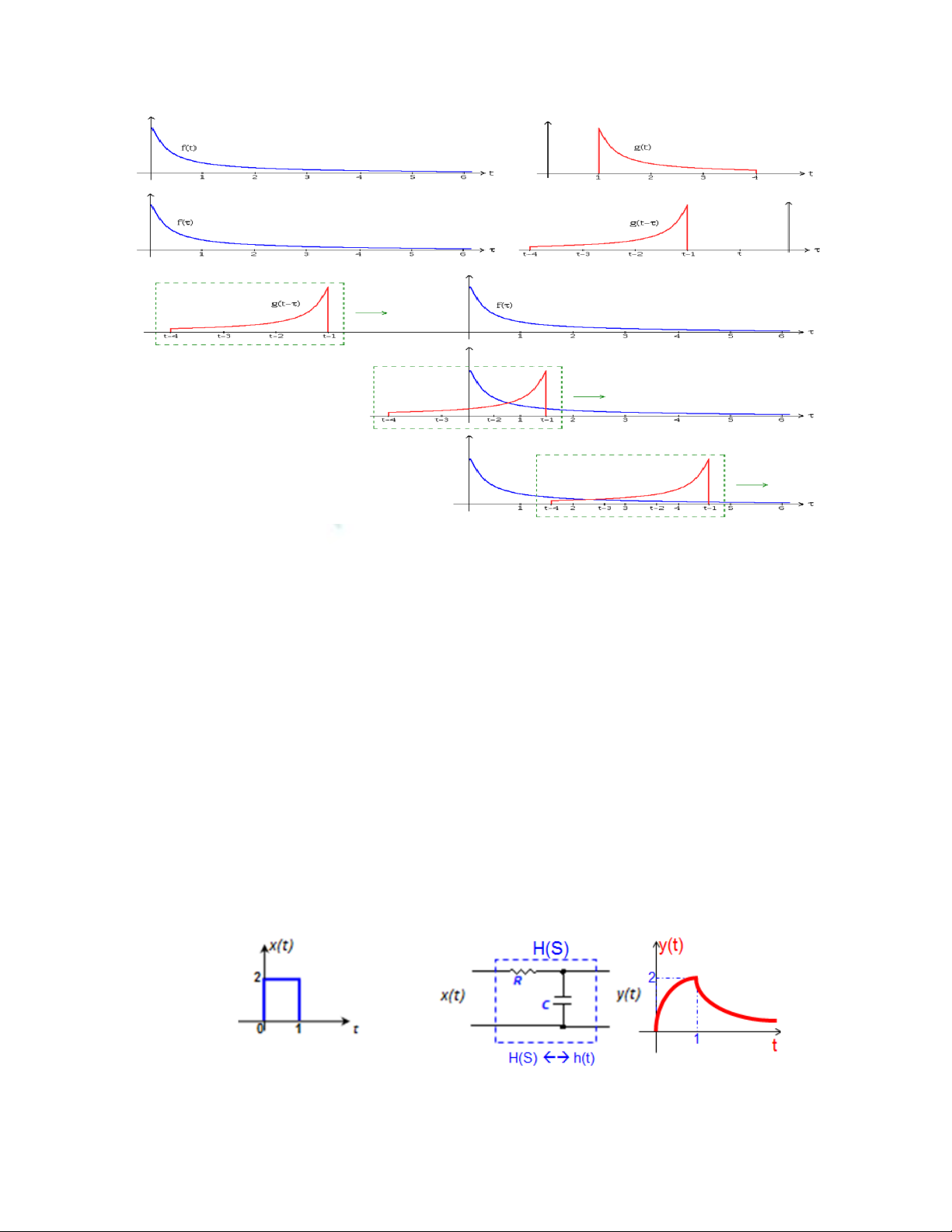
133
Hình 1: Cách tính tích chập
3. TÍNH CHẤT
1. x1(t) * x2(t) = x2(t) * x1(t)
2. x1(t) * [x2(t) * x3(t)] = [x1(t) * x2(t)] * x3(t)
3. x1(t) * [x2(t) + x3(t)] = x1(t) * x2(t) + x1(t) * x3(t)
4. a[x1(t) * x2(t)] = [ax1(t)] * x2(t)
5. Nếu x1(t) * x2(t)ϵ 𝐿2(-∞,+∞):∫𝑥1(𝑡).𝑥′2(𝑡−𝜏)
+∞
−∞ 𝑑𝑡 =x1(𝜏)*x’2(-𝜏)
4. ỨNG DỤNG
Tích chập được ứng dụng vào các lĩnh vực trong xác suất, thống kê, thị giác máy tính (computer vision), xử lý
ảnh, xử lý tín hiệu, kỹ thuật điện, học máy, và các phương trình vi phân.
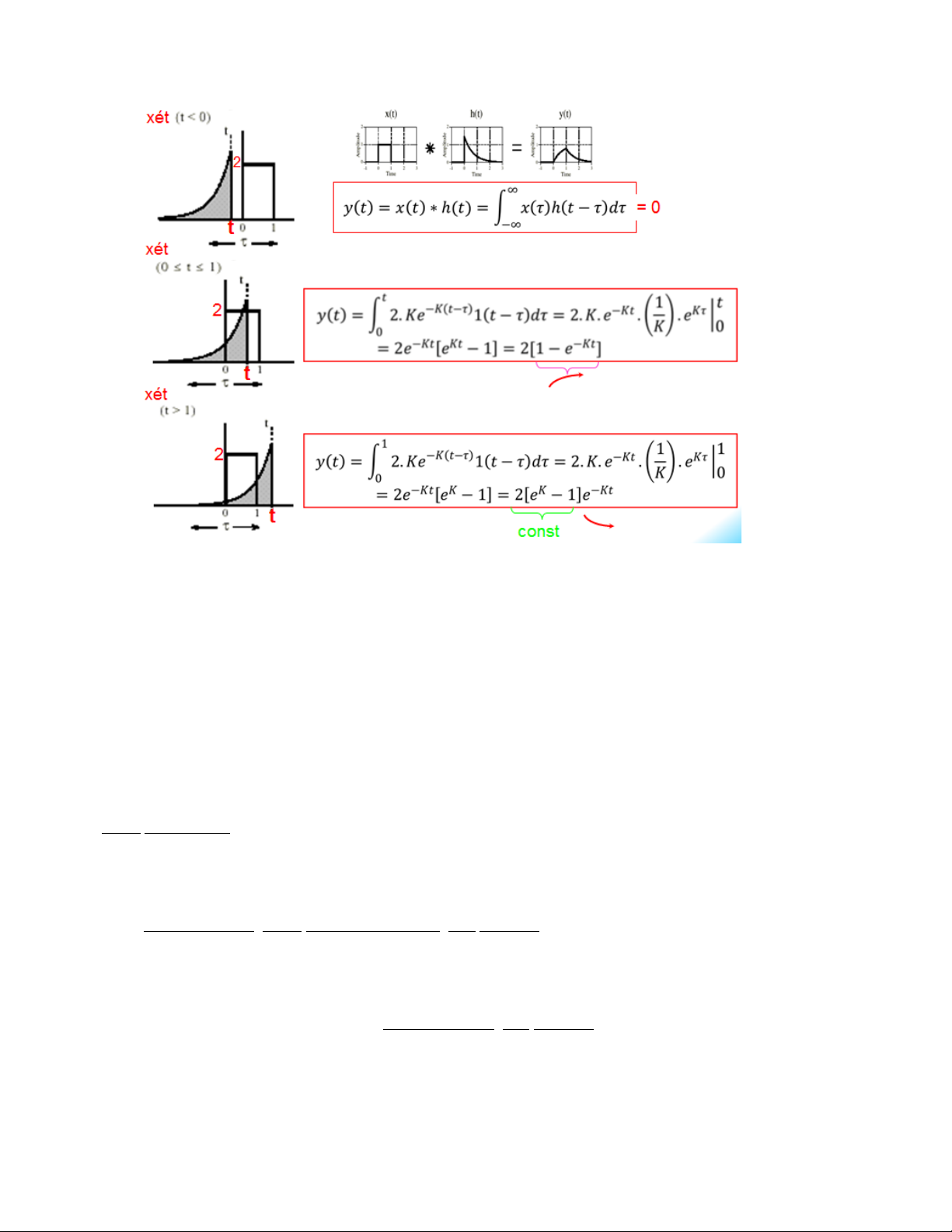
134
Hình 2: Ứng dụng tích chập tính cho mạch RC (LPF-Low Pass Filter)
5. KẾT LUẬN
Tích chập giúp ta giải quyết những vấn đề trong lĩnh vực điện tử - viễn thông tạo nên những bước nhảy vọt
trong lĩnh vực này càng phát triển.
TÀI LIỆU THAM KHẢO
[1] Bracewell, R. (1986), The Fourier Transform and Its Applications (ấn bản 2), McGraw
Hill, ISBN 0071160434.
[2] Hewitt, Edwin; Ross, Kenneth A. (1979), Abstract harmonic analysis. Vol. I, Grundlehren der
Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], 115 (ấn bản 2), Berlin,
New York: Springer-Verlag, ISBN 978-3-540-09434-0, MR 0551496.
[3] Hewitt, Edwin; Ross, Kenneth A. (1970), Abstract harmonic analysis. Vol. II: Structure and analysis for
compact groups. Analysis on locally compact Abelian groups, Die Grundlehren der mathematischen
Wissenschaften, Band 152, Berlin, New York: Springer-Verlag, MR 0262773.