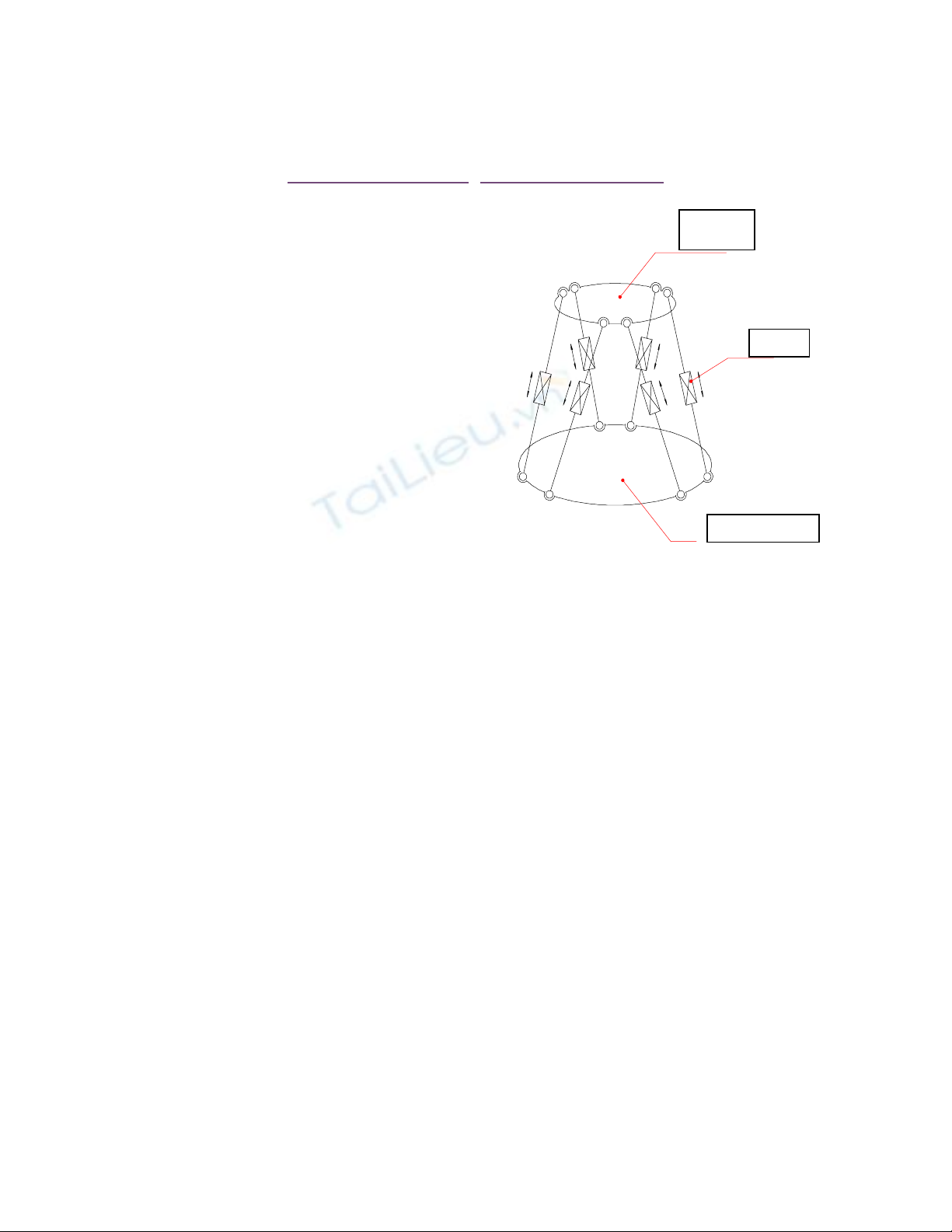
H
ình 1: Sơ đ
ồ
nguy
ê
n lý cơ c
ấ
u Stewart
platform
chân
T
ấ
m c
ố
đ
ị
nh
NHỮNG KẾT QUẢ CỨU BAN ĐẦU V Ề HEXAPOD
KS. Nguyễn Minh Tuấn
PGS.TS Đặng Văn Nghìn
nmtuan@dme.hcmut.edu.vn , dvnghin@dme.hcmut.edu.vn
Bộ môn Cơ Điện Tử - Khoa Cơ Khí, Trường Đại Học Bách Khoa Thành Phố Hồ Chí Minh
TÓM TẮT
Bài báo trình bày những kết quả nghiên cứu ban
đầu của chúng tô về HEXAPOD.
ABSTRACT
This paper introduces some pre-research results
of us about HEXAPOD.
1GIỚI THIỆU
1.1. GIỚI THIỆU VỀ HEXAPOD
Hiện nay trên thế giới HEXAPOD được sử dụng
rộng rãi trong các lĩnh vực sau:
• Dùng trong các hệ thống mô phỏng (máy
bay, xe hơi, nhà hát, …)
• Điều khiển các thiết bị y khoa
• Điều khiển các máy kinh vĩ trong xây
dựng
• Định vị các nguồn năng lượng (tia X,
laser, điện tử, quang, sóng, …)
• Định vị camera, kính thiên văn, vệ tinh
• Dùng trong máy công cụ để gia công các
bề mặt phức tạp…
Sở dĩ như vậy vì nó có những ưu điểm sau đây:
• Có thể định vị ở bất kỳ vị trí, hướng nào
trong không gian
• Kết cấu đơn giản, độ cứng vững cao
• Các quỹ đạo phức tạp và khó khăn của
phôi có thể được gia công trong một lần
gá
• Độ chính xác, ổn định cao
• Có thể tạo lực rất lớn và cứng vững nhờ
hệ thống chân thủy lực nhưng vận tốc
thấp
Vì khả năng vượt trội của cơ cấu 6 bậc tự do mà
có thể nói đây là một hướng nghiên cứu có giá trị
và có nhiều khả năng ứng dụng rộng rãi.
HEXAPOD được cấu tạo dựa trên nguyên tắc của
cơ cấu Stewart.
Cơ cấu được Stewart phát minh vào năm 1965 và
được mô tả trong hình 1. Nó gồm 6 chân có độ dài
thay đổi được, các chân này liên kết với giá và
platform bằng các khớp cầu. Bằng cách thay đổi
chiều dài các chân, ta có thể thay đổi vị trí và
hướng của platform trong không gian .
Kết cấu của nó giống như một bàn máy 6 chân.
1.2 MỤC ĐÍCH VÀ NỘI DUNG NGHIÊN CỨU
Mục đích nghiên cứu là thiết kế và chế tạo HEXAPOD
theo nguyên lý Stewart.
Nội dung nghiên cứu của đề tài bao gồm:
! Phân tích lựa chọn phương án thiết kế
! Giải các bài toán vị trí
o Bài toán động học ngược
o Bài toán động học thuận
! Phân tích ma trận jacobian
! Phân tích lực tĩnh và độ cứng vững
! Phân tích động học, động lực học
o Phân tích vận tốc
o Phân tích gia tốc
! Đưa ra một số phương án kết cấu cho chân máy
và hình thành giải pháp cho vấn đề điều khiển
song song các cơ cấu chấp hành.
1.4 PHÂN TÍCH VÀ CHỌN PHƯƠNG ÁN THIẾT KẾ
Hiện nay trên thế giới ứng dụng nguyên lý stewart có hai
phương án sau:
Phương án 1: Ứng dụng nguyên lý Stewart vào các máy
gia công dưới dạng cơ cấu Stewart mang đầu dụng cụ di
chuyển trong không gian.
Hình 2: Cơ c
ấ
u Stewart mang đ
ầ
u dụng
cụ di chuyển trong không gian.
Phương án 2: Ứng dụng nguyên lý Stewart vào
các máy gia công dưới dạng cơ cấu Stewart mang
bàn máy di chuyển 6 bậc tự do trong không gian,
trục dụng cụ cố định.
Chúng tôi đã chọn cả 2 phương án cùng tính toán
và thiết kế song song.
2.MỘT SỐ KẾT QUẢ ĐẠT ĐƯỢC
2.1 BẬC TỰ DO CƠ CẤU
Số bậc tự do của cơ cấu:
F=λ
λλ
λ(n-j-1) + ∑
∑∑
∑fi – fp
Với λ: là bậc tự do của khâu trong không gian
(λ=6), n: là tổng số khâu trong cơ cấu, J: là tổng
số khớp trong cơ cấu, fI : là tổng số bậc tự do của
các khớp trong cơ cấu, fp : là tổng số bậc tự do
thừa của cơ cấu
"
F=6(14-18-1) + (12
×
3+6
×
1) – 6 = 6.
2.2 BÀI TOÁN ĐỘNG HỌC NGƯỢC
Chiều dài chân tại vị trí phân tích:
Phương án 1:
ii
B
B
A
ii RBA abp −+= 0
Phương án 2:
()
ii
B
B
A
B
A
ii RRBA abctp −+−= 0
với B
AR: Là ma trận xoay để đưa pháp vector của
platform về trùng với trục z.
−
+−+
−−−
==
θθφφθ
ψθψφψθφψφψθφ
ψθψφψθφψφψθφ
φθψ
csscs
ssccscscsscc
csscccsssccc
RRRR zyzB
A
[]
T
iziyixi
Aaaa=a
[]
T
iwiviui
Bbbb=b
là các vector vị trí của các điểm Ai và Bi trong hệ tọa độ
A và B.
Lấy tích vô hướng của vector ii BA với chính nó cho ta
chiều dài của chân i tại vị trí đang phân tích
phương án 1:
()
[]
()
[]
ii
B
B
A
B
A
T
ii
B
B
A
B
A
iiiii
RRRR
BABAd
abctpatp −+−−+−
=⋅=
00 bc
2
phương án 2:
[][ ]
ii
B
B
A
T
ii
B
B
A
iiiii RRBABAd abpap −+−+=⋅= 00 b
2
3 CÁC KẾT QUẢ TÍNH TOÁN ĐƯỢC
3.1 MA TRẬN JACOBIAN LÀ
[]
[]
×
==
T
T
x
b
xSb
JJJ
6
1
6
1
ss
s
T
6
T
1
-1
qMM
Ở đây bi và si biểu diễn vector i
PB và vector đơn vị
theo trục .
chaân
Giaù
Platform Ñaàu
g
ia coân
g
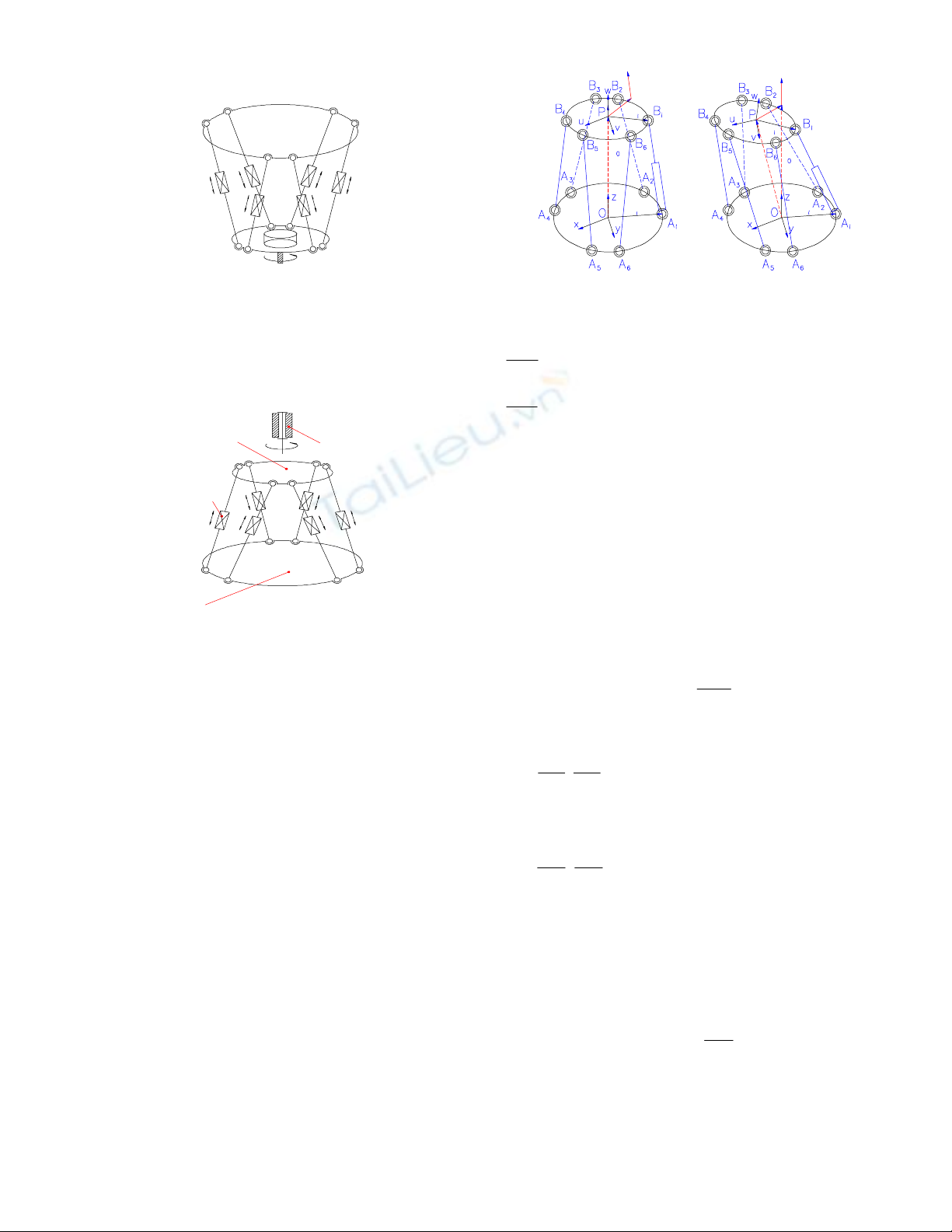
Hình 3: Cơ c
ấ
u Stewart mang bàn máy di
chuyển tự do trong không gian, trục dụng cụ cố
định.
H
ình 4: Mô hình phân tích tính toán chi
ề
u d
à
i
chân (phương án 2)
p
b
ct
n
ct
a
p
b
n
p
p
a

()
iy
i
iyiy
i
iyix
i
iIIvedm
ωω
&&
&21222 −−−−
()
]
21222 iy
i
iyiy
i
iyix
i
iIIvedm
ωω
&&
&−−−−
3.2 PHÂN TÍCH LỰC TĨNH
Phương trình cân bằng lực và moment của tấm di
chuyển tại điểm gia công như sau:
1.Hợp lực tác động lên tấm di chuyển
ii
fs
f
∑
=
2.Tổng moment của các lực tác động tại điểm gia
công
()
∑×= iii fsbn
Cuối cùng ta có phương trình cho ta quan hệ
chuyển đổi giữa lực tạo ra ở điểm đầu cuối và các
lực tác động.
τ
61
6
1
61
61 ⋅=
×
=
=T
J
f
f
bxb M
K
K
ss ss
n
f
F
Do đó nếu các lực tác động cho trước ta có thể
tính trực tiếp lực tạo ra ở điểm đầu cuối, và ngược
lại nếu cho trước lực ở điểm đầu cuối ta có thể tìm
đáp ứng lực trên các chân bằng biến đổi ngược.
3.3 PHÂN TÍCH ĐỘ CỨNG VỮNG
Ma trận độ cứng
[]
[]
×
×
××
=
T
T
b
b
bb
kK
66
11
61
61
1
1
61 ss
ss
ss ss
T
T
MM
K
K
3.4 ĐỘNG HỌC
Vận tốc: vận tốc góc của chân I
−
=
0
v
v
d
1
bix
i
iy
i
i
i
i
ω
Một khi tìm được vận tốc góc của chân i, vector
vận tốc khối tâm của piston và xylanh i là
i
i
i
ivv 21 xác định
Gia Tốc
Gia tốc góc của chân i
⋅
−
+−
=
=
0
.2
.2
1
0i
bix
i
biz
i
bix
i
i
biy
i
biz
i
biz
i
i
iy
i
ix
i
i
i
d
vv
v
d
vv
v
d&
&
&
&
&
ω
ω
ω
Một khi gia tốc góc của chân thứ i tìm được, gia tốc của
khối tâm piston và xylanh tìm được
+
−
−
−
=
i
biy
i
bix
ii
bix
i
biz
i
biy
i
i
bix
i
biz
i
bix
i
i
i
d
vv
d
vv
v
d
vv
v
d
e
22
1
1
1
.2
.2
&
&
v
()
()
()
+
+
+−
+−
=
i
biy
i
bix
i
biz
i
i
biy
i
biz
i
biy
i
i
i
bix
i
biz
i
bix
i
i
i
i
i
d
vve
v
d
vve
ved
d
vve
ved
d22
2
2
2
2
2
2
2
2
1
&
&
&
&
v
3.5 ĐỘNG LỰC HỌC
Động lực học chân
Phương trình động lực học cho chân i
()
ix
i
iciic
i
bix
ivemsgedmsgem
d
f1112211
[
1&
−−+=
θθ
()
ix
i
iciic
i
biy
ivemsgedmsgem
d
f1112211
1&
−−+=
θθ
Ở đây jix
I và jiy
I là thành phần x và y của moment
quán tính chính của xylanh (j=1) và piston (j=2) đối với
khối tâm tương ứng trong hệ tọa độ chân i.
Động lực học tấm di chuyển
()
pxp
6
1i
iibiz
i
ibiy
i
iibix
ivmscfsfccf &
=+−
∑
=
φφφθφ
()
pyp
6
1i iibiz
i
ibiy
i
iibix
ivmssfcfcsf &
=++
∑
=
θφφθφ
()
cppzp
6
1i ibiz
i
ibix
igmvmcfsf +=+−
∑
=
&
θθ
=×=
0
1
11 biy
i
bix
i
i
i
i
i
i
i
iv
v
d
e
esv
ω
,
=
i
i2
v
()
()
−
−
i
biy
i
i
bix
i
i
ivd
ved
ved
d2
2
1

Hình 5: T
ấ
m platform mang dụng cụ gia công
Lực phát động và phản lực nền
Khi các phản lực ở các khớp cầu đã tìm được, dễ
dàng xác định lực phát động i
τ
bằng cách lấy
tổng các lực tác động lên piston i theo trục zi
iz2
i
2ic2biz
i
ivmcgmf &
++=
θτ
Các phản lực tại khớp cầu Ai có thể tìm nhờ
phương trình Newton cho các chân
()
i2
i
2i1
i
1
A
A
i
21bi
i
ai
immRmm vvg
f
f
&& +=+++
4 PHƯƠNG PHÁP ĐIỀU KHIỂN
Đối với vấn đề điều khiển, giải pháp điều khiển đề
nghị ở đây nhằm giải quyết vấn đề điều khiển
song song các cơ cấu chấp hành là sử dụng 6
mạch điều khiển dùng vi điều khiển 8951 điều
khiển quá trình thực thi các dữ liệu vị trí, động
học và động lực học, các dữ liệu này được máy
tính tính toán sau đó sẽ truyền cho mạch vi điều
khiển để xử lý vấn đề điều khiển. Ưu điểm của
phương pháp này là chuyển nhiệm vụ điều khiển
từ máy tính xuống cho mạch phần cứng đảm
nhiệm nên việc điều khiển dễ dàng và hiệu quả
hơn. Máy tính lúc này chủ yếu dùng để giải quyết
vấn đề nội suy và tính toán các dữ liệu điều khiển.
MÔ HÌNH CHẾ TẠO
phương án 1
phương án 2
5 KẾT LUẬN VÀ HƯỚNG PHÁT TRIỂN
5.1 KẾT LUẬN
Qua quá trình nghiên cứu lý thuyết cũng như thực hiện
một số thử nghiệm, chúng tôi xin được có một số kết
luận như sau :
Chúng tôi đã xây dựng cơ sở toán học cho các quá trình
tính toán cơ bản của Hexapod, đưa giải pháp điều khiển
song song, chế tạo mô hình trên cơ sở thử nghiệm, gia
công với vật liệu mềm, công suất nhỏ.
5.2 HƯỚNG PHÁT TRIỂN
Trên cơ sở những nghiên cứu trên, chúng tôi chế tạo mô
hình phục vụ cho việc nghiên cứu thực nghiệm với các
vấn đề liên quan như :
# Giải thuật nội suy và mô phỏng quá trình gia công
của máy
• Nghiên cứu kỹ thuật điều khiển đa luồng, sử
dụng nhiều chip CPU để điều khiển song song
thục sự.
• Tiếp tục nâng cao tính linh hoạt của chương
trình và khả năng xử lý bản vẽ CAD 3D
• Xây dựng các giải thuật cho phép liên kết với
các phần mềm CAD khác như Pro-Engineer,
3D Max, Cimatron…
# Xây dựng mô hình xác định sai số của máy và khả
năng nâng cao độ chính xác
# Các vấn đề tối ưu hoá vị trí, động học, động lực học,
kết cấu và điều khiển
Đây sẽ là những hướng nghiên cứu tiếp theo để hoàn
thiện nguyên lý này.
H
ình 6: T
ấ
m platform l
à
bàn máy di chuy
ể
n

TÀI LIỆU THAM KHẢO
[1] Ngô Diên Tập,Vi Xử Lý Trong Đo Lường
Và Điều Khiển,Nhà xuất bản khoa học và
kỹ thuật, 1999.
[2] Nguyễn Thiện Phúc, Người Máy Công
Nghiệp Và Sản Xuất Tự Động Linh Hoạt,
Nhà xuất bản khoa học và kỹ thuật, 1991.
[3] X. M. Targ, Giáo Trình Giản Yếu Cơ
Học lý Thuyết, Nhà xuất bản đại học và
trung học chuyên nghiệp, 1983.
[4] Tống Văn On,Truyền Dữ Liệu, Trường
đại học Bách Khoa, 1993.
[5] Devdas Shetty, Richard A. Kolk,
Mechatronics System Design, PWS
Publishing Company, 1997.
[6] Francis C. Moon, Applied Dynamics
With Applications to Multibody and
Mechatronics Systems, John Willey&
Sons, Inc 1998.
[7] K.S. Fu, R.C. Gonzalez, C.S.G. Lee,
Robotics Control, Sensing, Vision, And
Intelligene, McGraw-Hill, Inc 1987.
[8] Lorenzo Sciavicco, Bruno Siciliano,
Modeling And Control of Robot
Manipulators, McGraw-Hill, Inc 1996.
[9] Lung-Wen Tsai,Robot Analysis, Wiley-
Interscience Publication 1999.
[10] T. D. Burtonm, Introduction to Dynamic
Systems Analysis, McGraw-Hill, Inc
1994.











![Bài tập tối ưu trong gia công cắt gọt [kèm lời giải chi tiết]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20251129/dinhd8055/135x160/26351764558606.jpg)













