Phương pháp tích hợp cơ sở tri thức xác suất dựa trên lý thuyết Demspter-Shaper hiệu quả

Tuyển tập Hội nghị Khoa học thường niên năm 2023. ISBN: 978-604-82-7522-8

PHƯƠNG PHÁP TÍCH HỢP CƠ SỞ TRI THỨC XÁC SUẤT

DỰA TRÊN LÝ THUYẾT DEMSPTER-SHAPER

Nguyễn Văn Thẩm

Trường Đại học Thủy lợi, email: thamnv@tlu.edu.vn

1. GIỚI THIỆU CHUNG

Với sự phát triển của công nghệ máy tính,

Internet và các lĩnh vực liên quan khác, công

nghệ tổng hợp thông tin đã và đang phát triển

vượt bậc. Việc thực hiện hợp nhất thông tin

cần phải xử lý rất nhiều thông tin không chắc

chắn. Các công cụ lý thuyết hiện có để xử lý

thông tin không chắc chắn bao gồm lý thuyết

xác suất, lý thuyết tập mờ, lý thuyết bằng

chứng Dempster-Shafer, lý thuyết entropy

thông tin. Lý thuyết Dempster-Shafer là một

công cụ điển hình và được sử dụng rộng rãi

để xử lý thông tin không chắc chắn và hợp

nhất dữ liệu, và nó được sử dụng rộng rãi

trong các lĩnh vực khác nhau.

Bài báo đề xuất một mô hình tích hợp cơ sở

tri thức (CSTT) xác suất bằng cách kết hợp lý

thuyết xác suất và một số luật hợp nhất được

phát triển từ lý thuyết Demspter-Shaper.

2. NỘI DUNG

2.1. Một số khái niệm

Đặt





E, ,E

là một tập hợp các sự

kiện được biểu thị trong không gian mẫu .

Với F, G , đặt FG là giao của F và G, F

là phủ định của F. Let 12

ΘEE

ˆˆ ˆ

E

n là hội

đầy đủ của



 với





E,Eii

. Đặt h=2n và





ΓΘ,,Θ

 là tập các hội đầy đủ của 

và 12 n

E E …E =. Hội đầy đủ thỏa mãn U, kí

hiệu ΘU, nếu U xuất hiện dương trong Θ.

Định nghĩa 1. [1] Hàm







0,1

:Γ m

được gọi là phép gán xác suất cơ bản (Basic

probability assignment-BPA) nếu thỏa mãn

các tính chất sau:

(i)







m

(ii)

















Hàm







0,1

:Γ  được gọi là độ đo

xác suất của



trên





Γ nếu:





ΕΘ

ΘΕ







m

Định nghĩa 2. [2] Đặt F, G  and



0,1







. Một ràng buộc xác suất (RBXS) là

một biểu thức có dạng







c trong đó





|cFG.

Định nghĩa 3. [2] Một cơ sở tri thức

(CSTT) xác suất  là một tập hữu hạn các

RBXS:





1,,



n

trong đó,









iii

cin

Định nghĩa 4. [2] Một hồ sơ TTXS 

trên tập các sự kiện



 là một bộ , ,

trong đó



 là một tập hữu hạn gồm n sự

kiện và  là một đa tập hữu hạn gồm h

CSTT xác suất.

Định nghĩa 5. [2] Một hồ sơ TTXS

,



 là hồ sơ TTXS nhất quán nếu và

chỉ nếu



:  nhất quán.

Đặt









U=1 nếu ΘU, ngược lại









U=0. Đặt







nh

 là ma trận đặc

trưng của CSTT xác suất , trong đó













ij ,1 ,



 



ii j i ii j i

aFG FG .

Định lý 1. [2] Cho CSTT xác suất . Một

BPA của  tương ứng với lời giải tối ưu *





của bài toán tối ưu:

(,) 1

ainrg m













hn

Tuyển tập Hội nghị Khoa học thường niên năm 2023. ISBN: 978-604-82-7522-8

với các ràng buộc:

0, 0

 

 





1, 0, 0

 



 

 



Định lý 2. [2] Đặt F, G . Hàm





0,1

:Γ  thỏa mãn các luật xác suất:

(P0)



ΘΓ ,ΘF











(P1)







ΘΓ ,ΘFG











(P2)













FG G F G

2.2. Một số luật hợp nhất

Định nghĩa 6. [1,3] Đặt 1

m và 2

m là hai

BPA, luật Dempster (Dempster Rule) DSR

được định nghĩa như sau:



0NÕu 



Ng−îc ¹

1 l















trong đó,



 

  



mm ,1,ij h







 

  



mm ,1,ij h

Định nghĩa 7. [1,3] Đặt 1

m và 2

m là hai

BPA, luật hợp tổng quát (Generalized

Combination Rule) GCR được định nghĩa

như sau:

  



12 NÕu 



Ng−îc l



1 i

 











trong đó,



1 m







12 1

 







 

  



mm và



 

  



mm ,1,ij h

Định nghĩa 8. [1] Đặt 1

m và 2

m là hai

BPA, luật hội chuyển TCR (Transferable

Conjunctive Rule) được định nghĩa như sau:

  



 

  



mmm

trong đó

 



0NÕu 



g−îc



1l¹ ,2







 







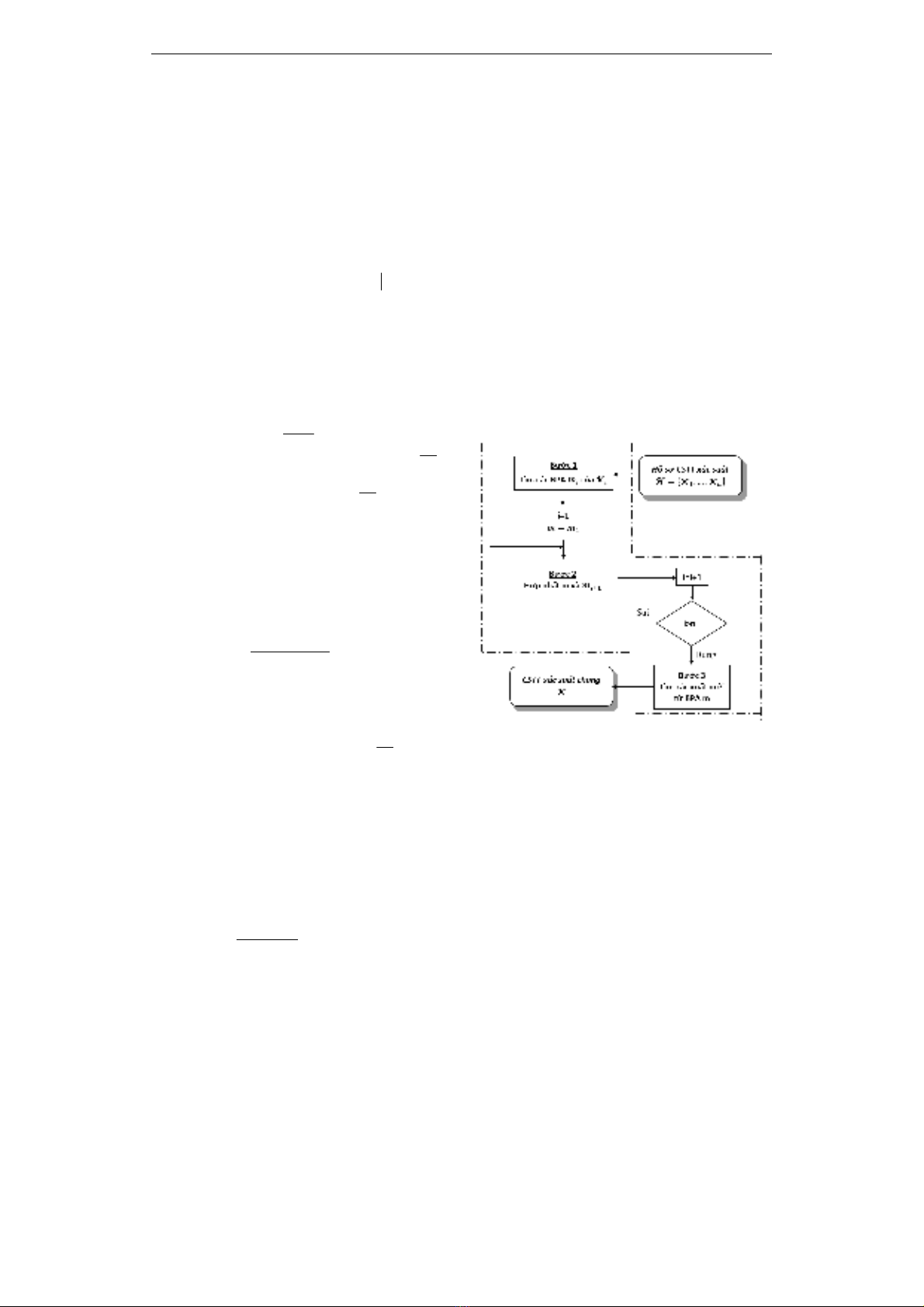
2.3. Mô hình đề xuất

Bài toán tích hợp các CSTT xác suất dựa

trên khoảng cách được định nghĩa:

(1) Đầu vào: Một hồ sơ CSTT xác suất.

(2) Đầu ra: Một CSTT xác suất.

(3) Phạm vi bài toán: CSTT được biểu

diễn bằng ràng buộc xác suất.

(4) Tiến trình tích hợp:

- Bước 1: Tìm các BPA của mỗi CSTT

trong hồ sơ CSTT xác suất  theo Định

lý 1.

- Bước 2: Hợp nhất các BPA theo các

Định nghĩa 6, 7, 8.

- Bước 3: Tìm xác suất mới sau tiến trình

tích hợp theo Định lý 2.

Mô hình tổng quát tích hợp các CSTT khả

năng được minh họa như Hình 1.

Hình 1. Mô hình tích hợp CSTT xác suất

2.3. Ví dụ tính toán và thảo luận

Vietnam Airlines thực hiện một cuộc khảo

sát về các chuyến bay bằng cách lấy ý kiến

của khách hàng, tiếp viên và phi công (gọi

chung là các chuyên gia). Họ được yêu cầu

đưa ra một số nhận định (tri thức) về: Tỷ lệ

để một chuyến bay theo lịch trình khởi hành

đúng giờ (D), tỷ lệ một chuyến bay đến đúng

giờ (A); và tỷ lệ một chuyến bay đến đúng

giờ khi khởi hành đúng giờ là (A|D).

Tuyển tập Hội nghị Khoa học thường niên năm 2023. ISBN: 978-604-82-7522-8

Từ kết quả của các chuyên gia cung cấp, ta

thu được hồ sơ CSTT xác suất gồm hai cơ sở

tri thức 1

 và 2

 được thể hiện trong Bảng 2

cùng với giá trị xác suất mong đợi (MĐ) của

mỗi RBXS trong CSTT xác suất sau tiến

trình tích hợp.

Bước 1: Tìm các BPA của 1

 và 2

. Theo

Định lý 1,



1234

,,,







,



123







.

00 11

0.4 0.6 0.4 0.6

0.5 0.5 0 0







 







A

BPA của 1

 tương lời giải tối ưu *





của

bài toán tối ưu:

43 123

(,)

amrg in















R

với các ràng buộc:

0, 0, 0 1,3

  

  



AA i



1234

1, 0 1, 4

 

 

Kết quả được thể hiện trong Bảng 1.

Bước 2: Hợp nhất các BPA theo các Định

nghĩa 6, 7, 8. Kết quả thể hiện trong Bảng 1.

Bảng 1. Các các BPA của 1

 và 2



i 1

m 2

m DSR GSR TCR

AD 0.4 0.4 0.20 0.18 0.16

AD 0.4 0.6 0.71 0.73 0.64

AD 0.2 0 0.09 0.09 0.08

 0 0 0.00 0.00 0.12

Bước 3: Tìm xác suất mới. Xét luật DSR,

theo luật (P0),





= 0.91,







D0.29.

Theo luật (P1) và (P2),



AD0.69. Kết

quả thể hiện trong Bảng 2.

Bảng 2. CSTT xác suất trước

và sau tiến trình tích hợp

c 1

 2

MD DSR GSR TCR



A 1.0 1.0 1.0 0.91 0.91 0.80



D 0.6 0.4 0.5 0.29 0.27 0.24



AD 0.5 0.5 0.5 0.69 0.67 0.67

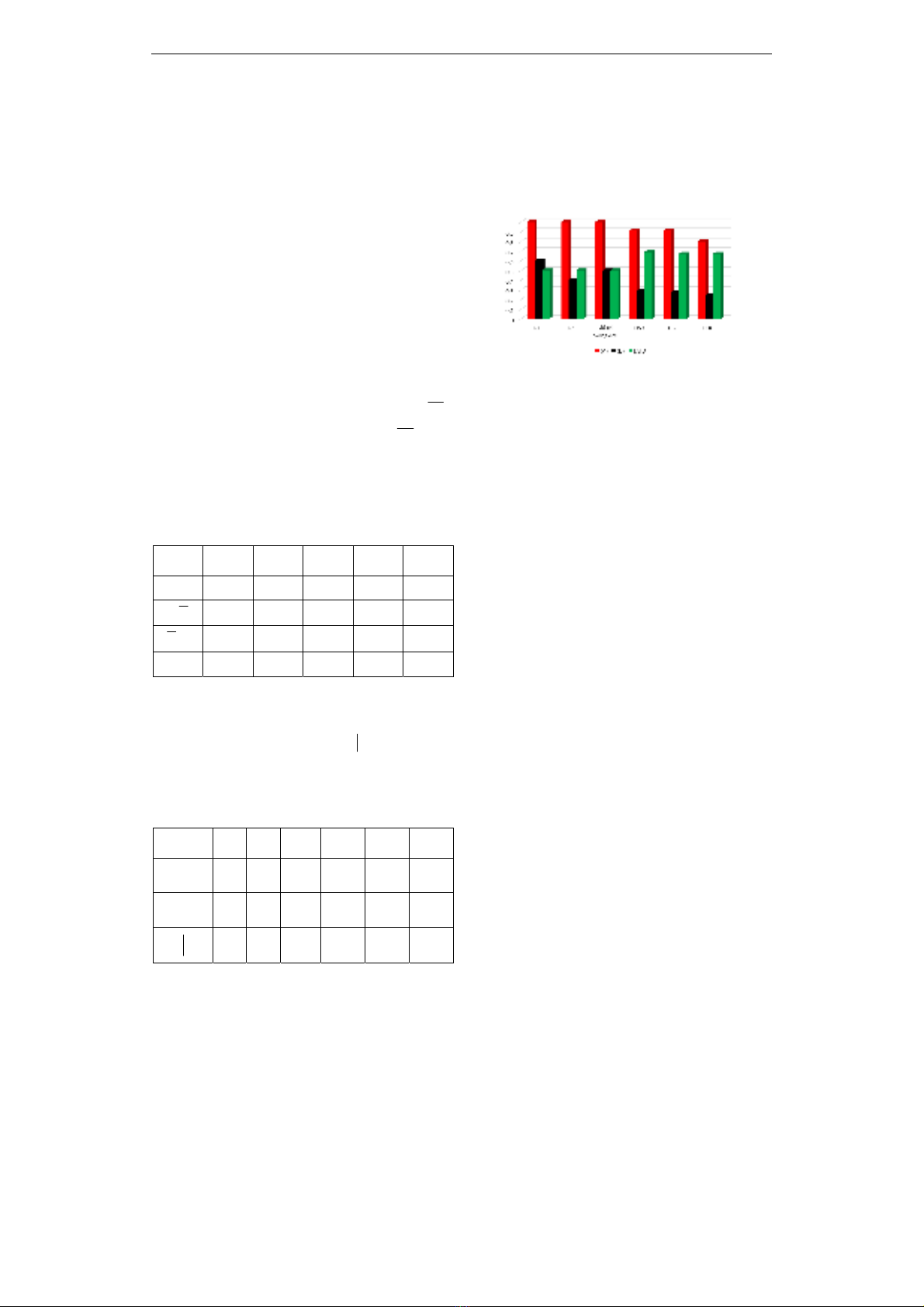
Hình 2 thể hiện kết quả thu được sau tiến

trình tích hợp CSTT xác suất và cho thấy khi

áp dụng các luật hợp nhất thì giá trị xác xuất

của các RBXS (A) và (A|D) kết quả có giá trị

gần với kết quả mong muốn. Tuy nhiên, giá

trị xác suất của ràng buộc (D) có độ lệnh cao

so với giá trị mong đợi.

Hình 2. So sánh các kết quả tích hợp

3. KẾT LUẬN

Trong bài báo này, tôi đã đề xuất một mô

hình tích hợp các CSTT xác suất bằng cách

sử dụng ba luật hợp nhất được phát triển từ lý

thuyết Demspter-Shaper (luật DSR, luật GSR

và luật TCR) để hợp nhất các BPA của các

CSTT xác suất đầu vào. Từ BPA thu được,

tôi sử dụng các luật xác suất để thu được

CSTT xác suất kết quả được biểu diễn bằng

các RBXS. Tuy nhiên, bài báo mới tập trung

ở khía cạnh lý thuyết mà chưa xem xét bài

toán dưới góc độ thực hành. Do đó, tôi sẽ

xem xét bài toán tích hợp trên bộ dữ liệu thực

tế để kiểm thử các kết quả đề xuất.

4. TÀI LIỆU THAM KHẢO

[1] Gan, Dingyi & Yang, Bin & Tang,

Yongchuan. 2020. An Extended Base Belief

Function in Dempster–Shafer Evidence

Theory and Its Application in Conflict Data

Fusion. Mathematics.

[2] Van Tham Nguyen và công sự. 2021.

A model for building probabilistic

knowledge-based systems using divergence

distances. Journal of Expert Systems with

Applications. Elsevier.

[3] Zhang, J., Deng, Y. 2017. A method to

determine basic probability assignment in the

open world and its application in data fusion

and classification. Appl Intell 46, 934-951.

Phương pháp tích hợp cơ sở tri thức xác suất dựa trên lý thuyết Demspter-Shaper

Chủ đề:

Tài liệu liên quan

Tài liêu mới

AI tóm tắt

Giới thiệu tài liệu

Đối tượng sử dụng

Từ khoá chính

Nội dung tóm tắt

Hỗ trợ

Phương thức thanh toán

Theo dõi chúng tôi