B¸o c¸o tèt nghiÖp Ph¹m TuÊn Anh-T§H46
Khoa C¬ ®iÖn - - Tr−êng §HNNI-Hμ Néi
41
tiÕp xóc cã sù khuÕch t¸n ®iÖn tö tù do bëi sè l−îng c¸c ®iÖn tö ë ®©y kh¸c
nhau, lµm xuÊt hiÖn suÊt ®iÖn ®éng t¹i ®iÓm tiÕp xóc mµ ®iÖn tr−êng cña nã
chèng l¹i sù khuÕch t¸n ®iÖn tö tõ phÝa d©y cã sè l−îng ®iÖn tö tù do nhiÒu
sang d©y cã Ýt h¬n. Gi¸ trÞ suÊt ®iÖn ®éng tiÕp xóc phô thuéc vµo b¶n chÊt cña
hai d©y dÉn vµ nhiÖt ®é tiÕp xóc. MÆt kh¸c, nÕu ®èt nãng mét ®Çu cña d©y dÉn
th× ho¹t tÝnh cña ®iÖn tö tù do ë ®Çu ®èt sÏ t¨ng lªn, gi÷a hai ®Çu d©y còng suÊt
hiÖn suÊt ®iÖn ®éng, do ®ã dßng ®iÖn tö khuÕch t¸n tõ ®Çu nãng sang ®Çu l¹nh,
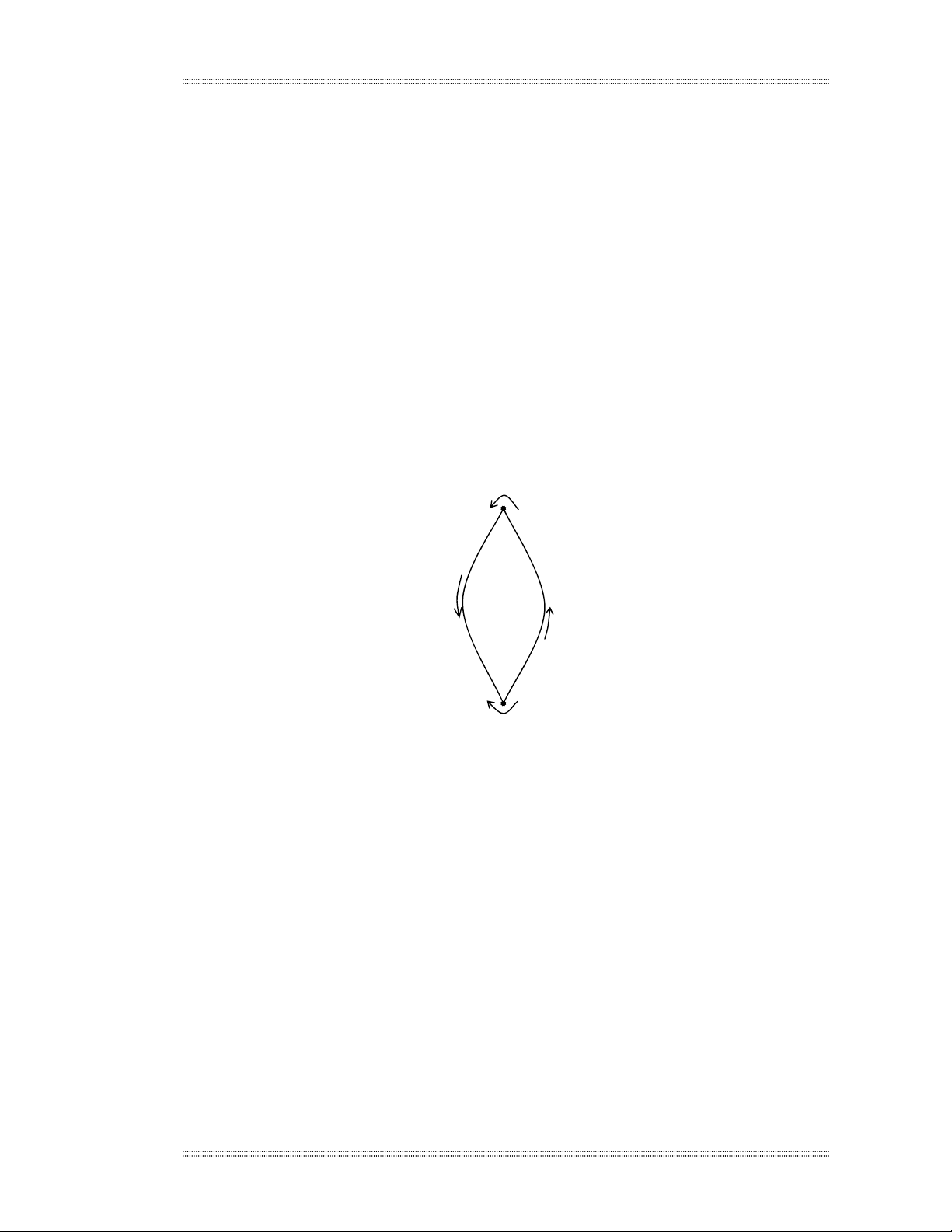
h×nh 2.16 m« t¶ sù h×nh thµnh suÊt ®iÖn ®éng trong vßng d©y A-B víi ®iÒu
kiÖn sè l−îng ®iÖn tö tù do cña d©y A(NA) lín h¬n sè l−îng ®iÖn tö cña d©y
B(NB), nhiÖt ®é ®Çu tiÕp xóc lµ t vµ ®Çu kia lµ t0 vµ t > t0.
H×nh 2.16. S¬ ®å søc ®iÖn ®éng
Theo ®Þnh luËt Kªich«p, søc ®iÖn ®éng trong vßng d©y ®−îc x¸c ®Þnh lµ:
E = eAB(t) - eA(t,t0) - eAB(t0) + eB(t,t0) (2-15)
Søc ®iÖn ®éng nµy sÏ sinh ra dßng ®iÖn ch¹y trong vßng d©y. Trong thùc
tÕ, gi¸ trÞ eA(t,t0) vµ eB(t,t0) rÊt nhá so víi eAB(t) vµ eAB(t0) nªn cã thÓ bá qua.
Khi ®ã søc ®iÖn ®éng lµ:
E = eAB(t) - eAB(t0) (2-16)
Nh− vËy, søc ®iÖn ®éng sinh ra trong c¸c vßng d©y tû lÖ víi hiÖu nhiÖt
®é ë hai ®Çu d©y. NghÜa lµ th«ng qua gi¸ trÞ suÊt ®iÖn ®éng E ®o ®−îc th× ta sÏ
biÕt ®−îc hiÖu nhiÖt ®é ë hai ®Çu d©y. Trong thùc tÕ, cÆp nhiÖt ®iÖn th−êng
®−îc sö dông ®Ó ®o mét m«i tr−êng hay vËt thÓ. NhiÖt ®é cña mét ®Çu ®−îc
eA(t,t0)eB(t,t0)
eAB(t)
eAB(t0)
B¸o c¸o tèt nghiÖp Ph¹m TuÊn Anh-T§H46
Khoa C¬ ®iÖn - - Tr−êng §HNNI-Hμ Néi
42
gi÷ cè ®Þnh, ®Çu nµy ®−îc gäi lµ ®Çu tù do hay ®Çu l¹nh, ®Çu cßn l¹i ®−îc ®Æt
vµo m«i tr−êng ®o nhiÖt ®é vµ ®−îc gäi lµ ®Çu lµm viÖc.
Ph−¬ng tr×nh c¬ b¶n cña cÆp nhiÖt ®iÖn lµm c¶m biÕn ®o nhiÖt ®é cã
d¹ng nh− sau:
E = f(T) (2-17)
ë ®iÒu kiÖn chuÈn khi chia ®é c¸c cÆp nhiÖt quy ®Þnh T0 = 00C. ViÖc sö
dông cÆp nhiÖt ®iÖn cã rÊt nhiÒu −u ®iÓm nh−: kÝch th−íc cÆp nhiÖt nhá nªn cã
thÓ ®o nhiÖt ®é ë tõng ®iÓm cña ®èi t−îng nghiªn cøu vµ t¨ng tèc ®é håi ®¸p.
mét −u ®iÓm næi bËt n÷a lµ cÆp nhiÖt ®iÖn cung cÊp suÊt ®iÖn ®éng nªn khi ®o
kh«ng cÇn cã dßng ch¹y qua vµ do vËy kh«ng cã hiÖu øng ®èt nãng.
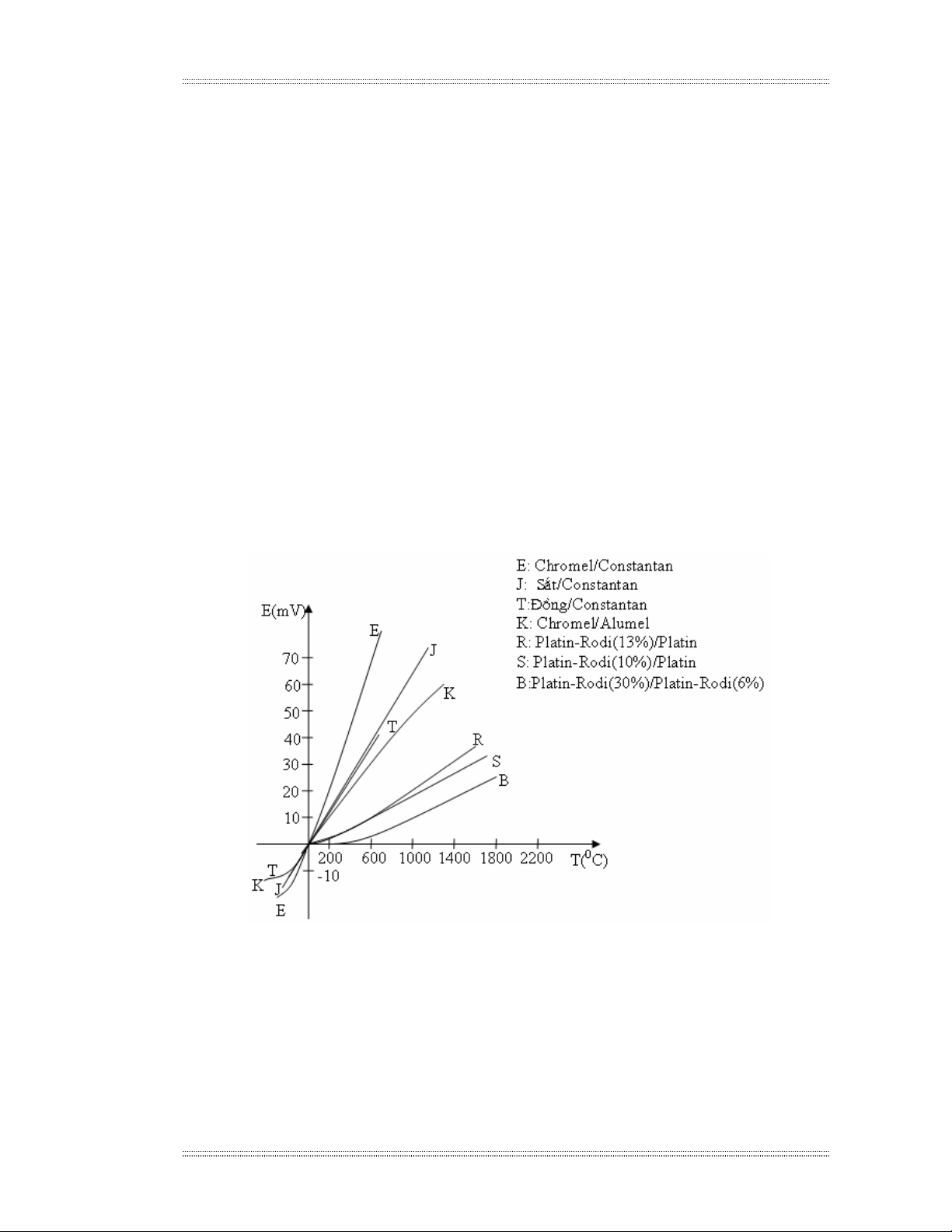
SuÊt ®iÖn ®éng cña cÆp nhiÖt trong mçi d¶i réng cña nhiÖt ®é lµ hµm
kh«ng tuyÕn tÝnh cña nhiÖt ®é cÇn ®o. §å thÞ biÓu diÔn sù thay ®æi suÊt ®iÖn
®éng E phô thuéc vµo nhiÖt ®é cña mét sè lo¹i cÆp nhiÖt nh− h×nh 2.17.
H×nh 2.17. Sù thay ®æi nhiÖt cña suÊt ®iÖn ®éng E cña
mét sè lo¹i cÆp nhiÖt ®iÖn
+ S¬ ®å ®o: ®Ó ®o søc ®iÖn ®éng E th× ph¶i ghÐp ®−îc thiÕt bÞ ®o (TBD)
vµo trong m¹ch cña cÆp nhiÖt ®iÖn. ViÖc ghÐp nèi nµy ph¶i ®¶m b¶o kh«ng lµm
thay ®æi gi¸ trÞ søc ®iÖn ®éng sinh ra trong cÆp nhiÖt ®iÖn. Trong thùc tÕ
B¸o c¸o tèt nghiÖp Ph¹m TuÊn Anh-T§H46
Khoa C¬ ®iÖn - - Tr−êng §HNNI-Hμ Néi
43
th−êng cã hai c¸ch ghÐp nèi cÆp nhiÖt ®iÖn ®ã lµ: ghÐp nèi qua ®Çu tù do vµ
ghÐp nèi qua mét ®iÖn cùc nhiÖt.
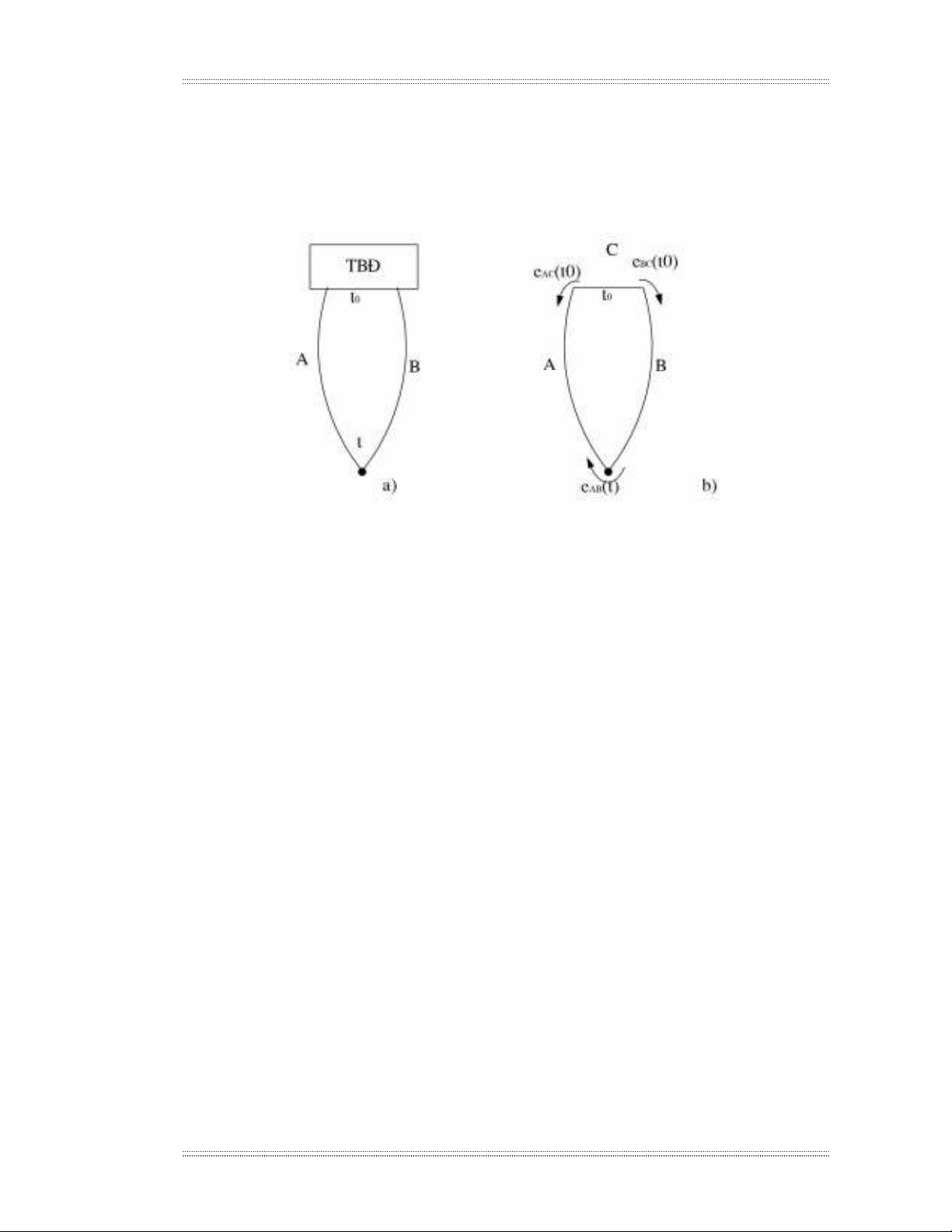
• GhÐp nèi qua ®Çu tù do ®−îc m« t¶ nh− h×nh sau:
H×nh 2.18. S¬ ®å nèi thiÕt bÞ ®o qua ®Çu tù do cña cÆp nhiÖt ®iÖn
a) M¹ch ®iÖn b) S¬ ®å t−¬ng ®−¬ng
Tõ m¹ch t−¬ng ®−¬ng, theo ®Þnh luËt Kiech«p cã:
E = eAB(t) – eAC(t0) + eBC(t0) (2-18)
Khi t=t0 trong vong d©y kh«ng tån t¹i dßng ®iÖn, khi ®ã E=0.
(2-18) => 0 = eAB(t0) – eAC(t0) + eBC(t0)(2-19)
=> eAB(t0) = eAC(t0) + eBC(t0) (2-20)
Nh− vËy ta cã:
E = eAB(t) - eAB(t0) (2-21)
NghÜa lµ thiÕt bÞ ®o kh«ng lµm thay ®æi suÊt ®iÖn ®éng sinh ra trong
vßng d©y.
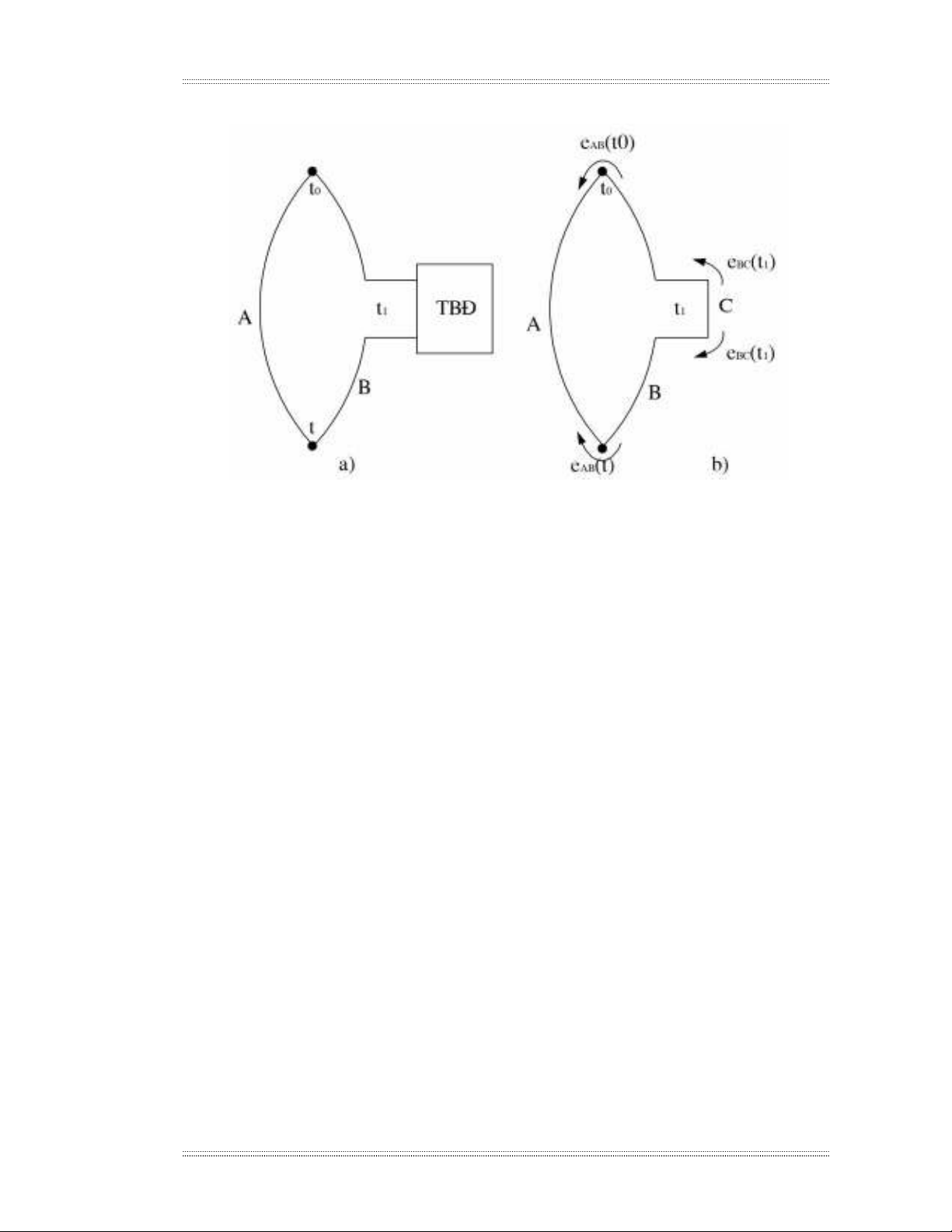
• GhÐp nèi TB§ trong ®iÖn cùc nhiÖt ®−îc m« t¶ nh− h×nh sau:
B¸o c¸o tèt nghiÖp Ph¹m TuÊn Anh-T§H46
Khoa C¬ ®iÖn - - Tr−êng §HNNI-Hμ Néi
44
H×nh 2.19. S¬ ®å nèi TB§ trong ®iÖn cùc nhiÖt
a) M¹ch ®iÖn b) S¬ ®å t−¬ng d−¬ng
Theo ®Þnh luËt Kiech«p ¸p dông ®èi víi s¬ ®å m¹ch t−¬ng ®−¬ng cã:
E = eAB(t) – eAB(t0) – eBC(t1) + eBC(t1) (2-22)
Hay E = eAB(t) – eAB(t0) (2-23)
VËy tõ hai c¸ch ghÐp nèi trªn thÊy E = eAB(t) – eAB(t0), nghÜa lµ thiÕt bÞ
®o kh«ng cã ¶nh h−ëng ®Õn tÝnh chÊt cña cÆp nhiÖt ®iÖn vµ ng−îc l¹i.
Trong thùc tÕ th× mét sè cÆp nhiÖt ®iÖn cã d¶i nhiÖt ®é lµm viÖc bÞ h¹n
chÕ, ch¼ng h¹n nh− ë nhiÖt ®é thÊp n¨ng suÊt nhiÖt ®iÖn cña nã gi¶m ®i lµm
cho tÝnh chÝnh x¸c trong phÐp ®o bÞ h¹n chÕ. ë nhiÖt ®é cao cã thÓ x¶y ra hiÖn
t−îng t¨ng kÝch th−íc h¹t tinh thÓ lµm t¨ng ®é dßn c¬ häc, thËm chÝ cã thÓ bÞ
nãng ch¶y hoÆc cã thÓ x¶y ra hiÖn t−îng bay h¬i mét trong c¸c thµnh phÇn
trong hîp kim lµm cÆp nhiÖt ®iÖn.
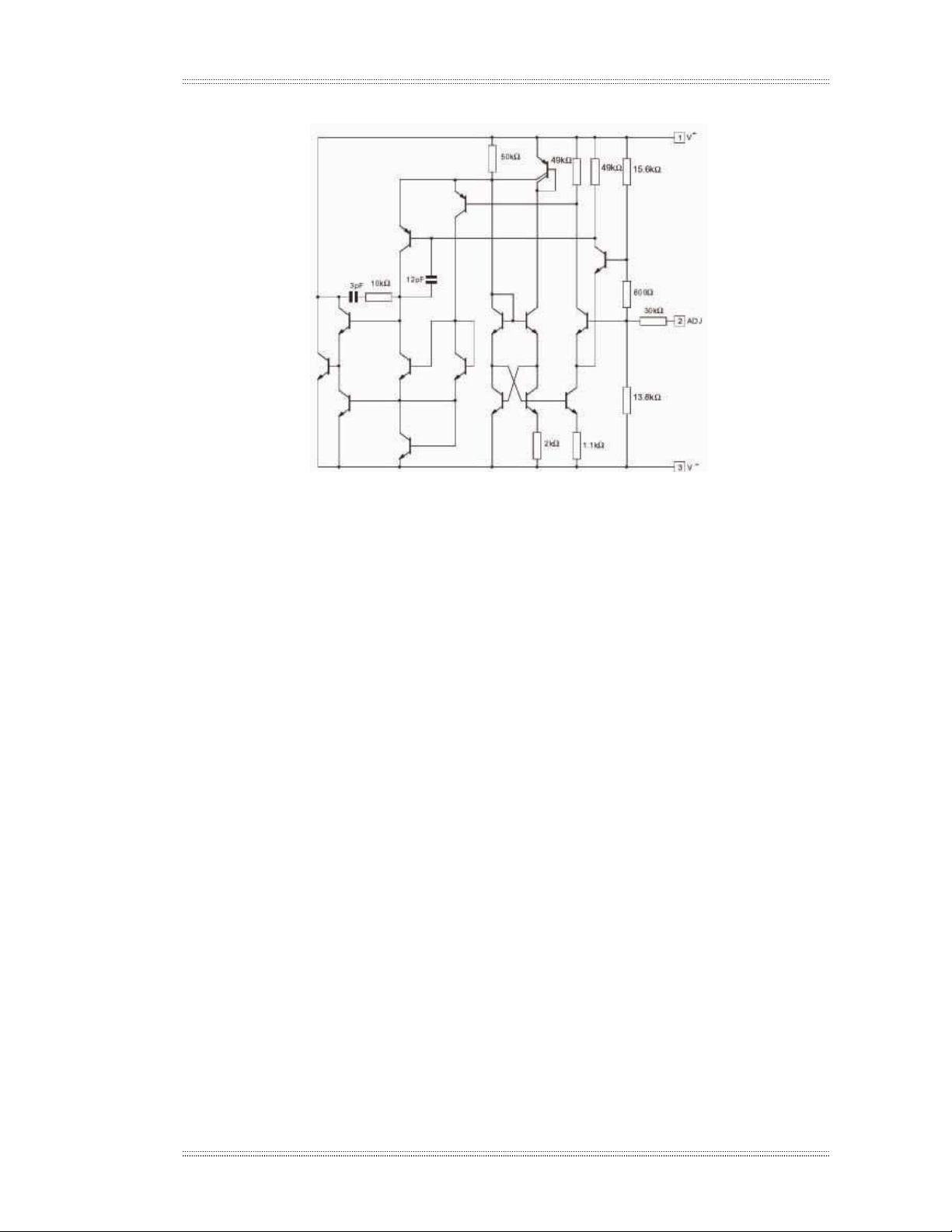
2.2.5.4. Khèng chÕ nhiÖt ®é b»ng c¶m biÕn vi m¹ch LM335
LM335 lµ lo¹i c¶m biÕn nhiÖt ®é chÝnh x¸c trong d¶i nhiÖt ®é tõ -400C
®Õn +1000C, nã lµm viÖc nh− hai Diode Zener vµ ®é biÕn thiªn ®iÖn ¸p theo
nhiÖt ®é lµ 10mV/10C. S¬ ®å cÊu t¹o bªn trong vi m¹ch LM335 cã d¹ng nh−
h×nh 2.20.
B¸o c¸o tèt nghiÖp Ph¹m TuÊn Anh-T§H46
Khoa C¬ ®iÖn - - Tr−êng §HNNI-Hμ Néi
45
H×nh 2.20. S¬ ®å cÊu t¹o vi m¹ch LM335
§Æc tuyÕn cña LM335 ®−îc m« t¶ nh− sau:
U =10×T (mV) = 2730 + 10
×
t (mV) = 2,73 + 0,01×t (V)
Trong ®ã:
T: lµ gi¸ trÞ nhiÖt ®é tÝnh theo nhiÖt ®é Kelvin (0K).
t: lµ gi¸ trÞ nhiÖt ®é tÝnh theo nhiÖt ®é Celsius (0C).
§Ó cho vi m¹ch lµm viÖc tin cËy vµ æn ®Þnh th× dßng ®iÖn cho phÐp qua
nã lµ A
μ
400 ®Õn 5mA. Khi lµm viÖc ë nhiÖt ®é 250C vµ dßng ®iÖn lµm viÖc lµ
1mA th× ®iÖn ¸p ra cña vi m¹ch n»m trong kho¶ng 2,94V ®Õn 3.04V. §Æc biÖt
lµ LM335 cã ®é chÝnh x¸c cao, tÝnh n¨ng c¶m biÕn nhiÖt ®é rÊt nh¹y, ch¼ng
h¹n nh− ë nhiÖt ®é 250C nã cã sai sè kh«ng qu¸ 1%.
Nh− vËy, trong qu¸ tr×nh tù ®éng ®iÒu khiÓn nhiÖt ®é, ®Ó cã thÓ ®iÒu
chØnh nhiÖt ®é theo ®óng yªu cÇu cña ®èi t−îng nghiªn cøu th× viÖc sö dông
nhiÖt kÕ d·n në chÊt láng vµ nhiÖt kÕ d·n në chÊt r¾n ®Ó ®iÒu chØnh nhiÖt ®é lµ
®iÒu hÕt søc khã kh¨n v× tÝnh −u viÖt cña nã kh«ng cao. MÆt kh¸c nhiÖt ®é lµ
mét ®¹i l−îng kh«ng ®iÖn, do ®ã ®Ó ®iÒu chØnh ®−îc nã mét c¸ch tuyÕn tÝnh
theo gi¸ trÞ ®Æt tr−íc th× ph¶i chuyÓn ®æi thµnh ®¹i l−îng ®iÖn, thiÕt bÞ dïng ®Ó
chuyÓn ®æi nhiÖt ®é thµnh ®¹i l−îng ®iÖn ®iÖn gäi lµ c¶m biÕn. V× vËy, ®Ó ®o
nhiÖt ®é trong tñ nu«i cÊy vi khuÈn mµ cã sö dông c¶m biÕn nhiÖt ®Ó ®o nhiÖt