http://www.iaeme.com/IJMET/index.asp 1584 editor@iaeme.com
International Journal of Mechanical Engineering and Technology (IJMET)
Volume 10, Issue 03, March 2019, pp. 1584–1592, Article ID: IJMET_10_03_159
Available online at http://www.iaeme.com/ijmet/issues.asp?JType=IJMET&VType=10&IType=3
ISSN Print: 0976-6340 and ISSN Online: 0976-6359
© IAEME Publication Scopus Indexed
REDUCING PITCH ANGLE AND SUSPENSION
JOUNCES OF A TRUCK WHEN BRAKING ON
RAILWAY CROSSING BY CONTROL OF SEMI-
ACTIVE SUSPENSION
N. L. Pavlov
Department of Combustion Engines, Automobile Engineering and Transport,
Faculty of Transport,
Technical University of Sofia, 8 Kliment Ohridski Blvd., 1000 Sofia, Bulgaria
ABSTRACT
This paper presents pith plane dynamic model of a cargo truck. Numerical
simulations for determination of a pitch angle and deflection in front and rear
suspension under braking on railway crossing are conducted. The change of the braking
force is presented by trapezoidal form, similar to the theoretical law of variation of
braking deceleration in the braking diagram of road vehicles. For the railway crossing
profile trapezoidal function is used too. The numerical simulations are carried out in
program field of MATLAB. After conducting tests for determination of a braking
dynamics and braking properties of a truck in road conditions, the pith plane model is
validated. Possibilities for pitch angle and suspension jounces reduction are given. A
fifth wheel assembly, displacement sensors and data acquisition system are used in the
road tests.
Key words: Dynamic model, truck, simulation and road test
Cite this Article: N. L. Pavlov, Reducing Pitch Angle and Suspension Jounces of a
Truck When Braking on Railway Crossing by Control of Semi-Active Suspension,
International Journal of Mechanical Engineering and Technology 10(3), 2019, pp.
1584–1592.
http://www.iaeme.com/IJMET/issues.asp?JType=IJMET&VType=10&IType=3
1. INTRODUCTION
Road transport and commercial vehicles are constantly being studied and improved, and proof
of this is the availability of various publications on the topic. Along with the fuel economy and
the exploitation efficiency of the road freight transport [1, 2 and 3], the problems of the
dynamics of commercial vehicles are a question of present interest [4, 5]. When the road
vehicles are under braking on the vehicle body acts a powerful disturbance as a torque. Its
magnitude is proportional to the inertia force and, on the other hand to the mass centre height
of the vehicle [6, 7 and 8]. The action of the torque is accompanied by longitudinal tilting of
the vehicle body (pitch angle) due to the presence of elastic suspension. This results in
N. L. Pavlov
http://www.iaeme.com/IJMET/index.asp 1585 editor@iaeme.com
redistribution the normal reactions of the front and rear wheels. The phenomenon is most
pronounced in vehicles with a short base and a high mass centre, for unladed trucks or tractors
with a detached semitrailer. When the ground vehicles brakes, the wheel suspension travel may
be spend and shocks may occur as a result of the inclusion of the jounce stops at maximum
suspension deflection [9]. The phenomenon is known as a suspension "slam" or "jounce", which
is an amalgamation of the words jump and bounce. In suspension terminology, it means the
most compressed condition of a spring. These phenomena are even more pronounced when
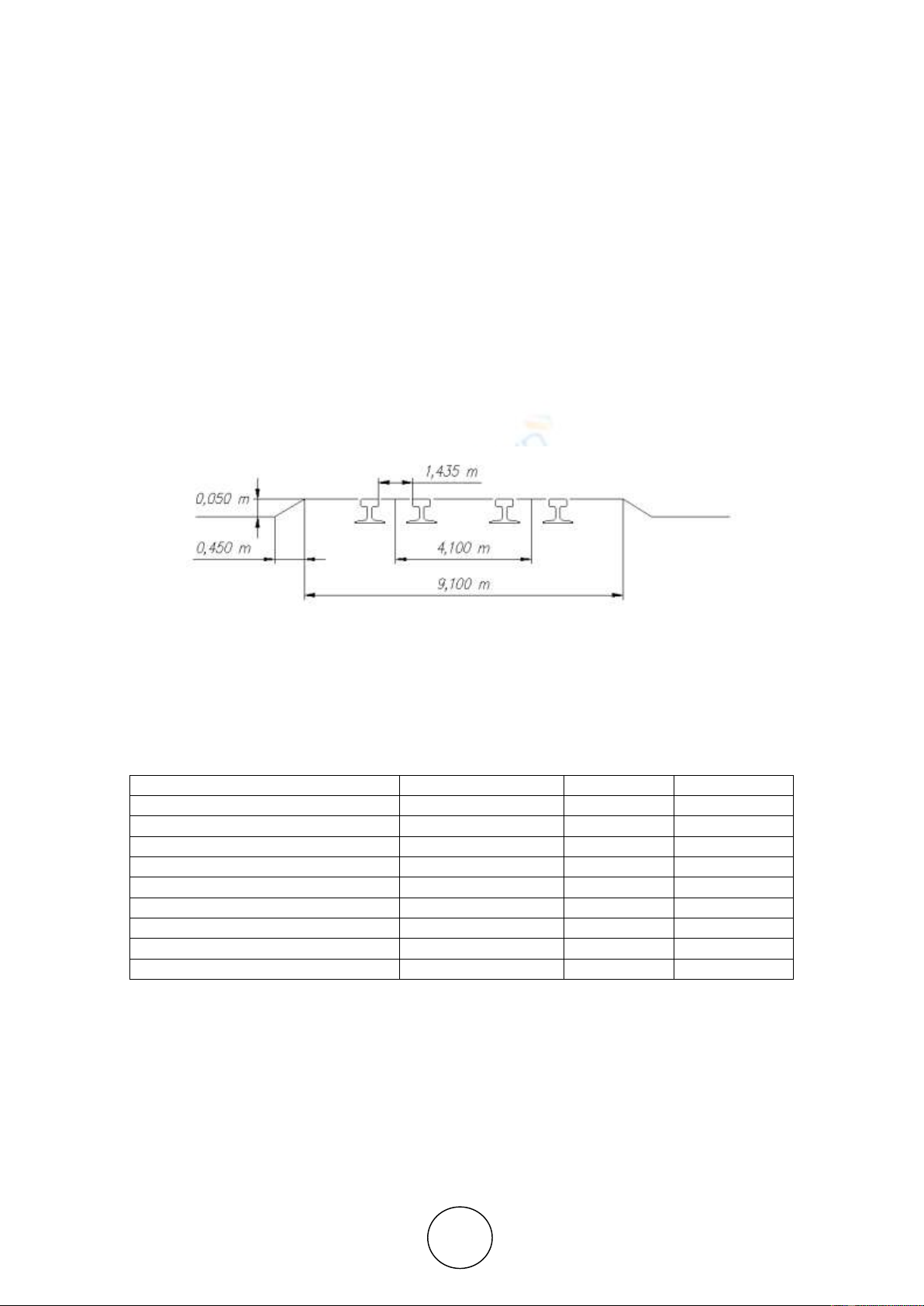
vehicle passing through convex irregularities such as some railway crossings (Fig. 1). This type
of crossings has a profile corresponding to a single bump of triangle or trapezoidal irregularity.
Figure 1 A primer of a railway crossing like single road irregularity
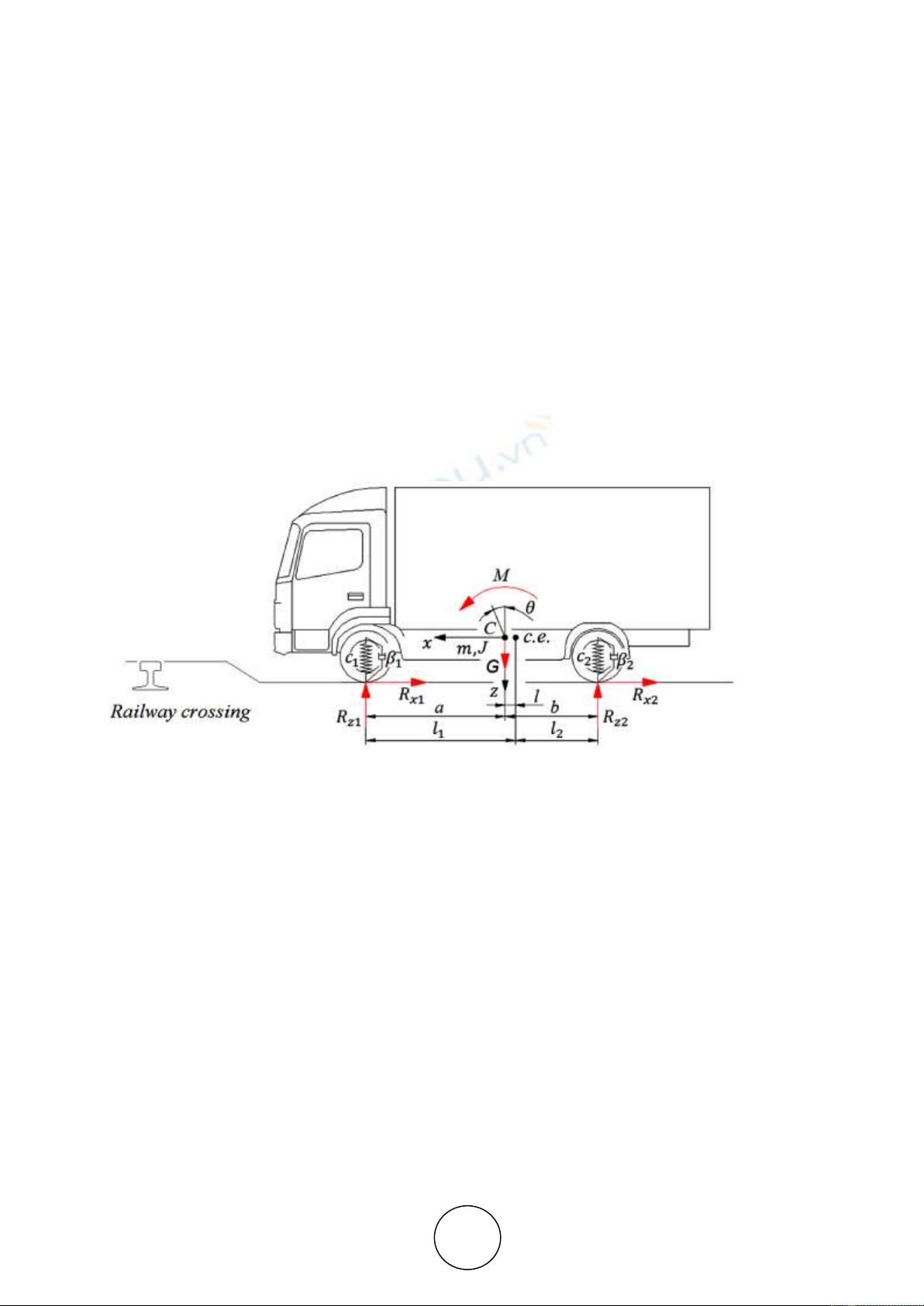
2. DYNAMIC MODEL
In order to find the pitch angle and the suspension deflection values when the truck
simultaneously braking and crossing over the railway, the dynamic model based on the authors’
model presented in [9] used to study the braking only, without any road irregularities. The
present model is shown in Fig. 2. It takes into account the mass of the vehicle, its moment of
inertia around the transverse axis, the elasticity of the front and rear suspension and the damping
of the shock absorbers. The railway crossing is presented as irregularity with trapezoidal form.
Figure 2 Dynamic model of a truck when braking on railway crossing
Braking is a process of creating and control the artificial resistance of the vehicle motion.
The braking of the vehicle is mainly accomplished by creating braking moments from the brake
Reducing Pitch Angle and Suspension Jounces of a Truck When Braking on Railway Crossing by
Control of Semi-Active Suspension
http://www.iaeme.com/IJMET/index.asp 1586 editor@iaeme.com
mechanisms on the wheels [10]. Due to friction in the contact path, a tangential reaction Rx
directed opposite of the direction of motion arises under the action of the braking moment. Then
in braking mode for the differential equation of motion along x-axis is obtained:
x
Rxm
(1)
Since the mass center of the vehicle lies above the center of elasticity of the suspension at
any distance, the inertia force that is always directed against the acceleration, in the case of
braking, creates torque. Because the trucks have elastic suspension of the body on the wheels,
the resulting torque deflects the suspension elastic elements and tilts the vehicle forward at an
angle θ around the center of elasticity – c. e. If the center of mass (m) is relocated to the point
C placed in the horizontal plane of the center of elasticity (c. e.) it will not affect linear z-axis
oscillations. To study the angular oscillations during braking, it is necessary to add the torque
(moment) M = Fj.h (Fig. 3). After reducing the inertial force Fj and relocating the center of
gravity to the plane of the center C, also is necessary to reduce the coordinate system in an
appropriate manner. This is accomplished by relocating the start of the x-z coordinate system
at a distance h, at point C, which is accepted as a new coordinate of the mass center.
Figure 3 Dynamic model after reduction of inertia force and adding the torque M = Fj.h
The torque M is added as a disturbance in the differential equation of the angular
displacement around the y-axis. The change of the braking torque is presented by trapezoidal
form, similar to the theoretical law of variation of braking deceleration in the braking diagram
of road vehicles. The differential equations of motion of vertical and angular displacements are:
22112211
2121
qqqcqc
bzcazcbzazzm
(2)
Mqbqabqcaqc
bzbcazacbzbazaJ
22112211
2121
(3)
where
1
q
and
2
q
are the coordinates of the road irregularities respectively under the front
and rear axle of the truck, and also their derivatives
1
q
and
2
q
, i.e. the velocities with which
the wheels of the truck are moved along the vertical axis.
For the inertia force can be writing:
N. L. Pavlov
http://www.iaeme.com/IJMET/index.asp 1587 editor@iaeme.com
21
.xxxj RRRjmF
(4)
where j is braking deceleration;
Rx1 and Rx2 are the longitudinal reactions in the contact between the wheels and the road under
braking.
In the used model the following assumptions have been accepted [9]:
- the characteristics of the elastic and damping elements are linear;
- the vehicle moves horizontally;
- the aerodynamic drag is ignored;
- the rolling resistance forces are ignored;
- the influence of the inertia moments of the rotating parts is ignored;
- the body angle is small (up to 15 °) and
,
1cos
.
The dimensions of the railway crossing are given in Fig. 4 below:
Figure 4 Dimensions of the railway crossing
3. NUMERICAL SIMULATIONS
The simulations were performed using MATLAB with the given in Table 1 parameters:
Table 1 Simulation parameters
Parameter
Symbol
Value
Unit
Full mass of the truck
m
7500
kg
Moment of inertia
J
33582
kg.m2
Front suspension stiffness
c1
166600
N/m
Rear suspension stiffness
c2
230625
N/m
Distance
h
1,2
m
Distance
a
2,32
m
Distance
b
1,93
m
Static load – front axle
Gw1
33,355
kN
Static load – rear axle
Gw2
40,221
kN
The minimal and maximal damping coefficients of suspension β1 and β2 are defined in the
work [9]. The accepted values for the front suspension are:
β1low=9520 N.s/m
β1high=30000 N.s/m
For the rear suspension:
Reducing Pitch Angle and Suspension Jounces of a Truck When Braking on Railway Crossing by
Control of Semi-Active Suspension
http://www.iaeme.com/IJMET/index.asp 1588 editor@iaeme.com
β2low=12300 N.s/m
β2high=35000 N.s/m
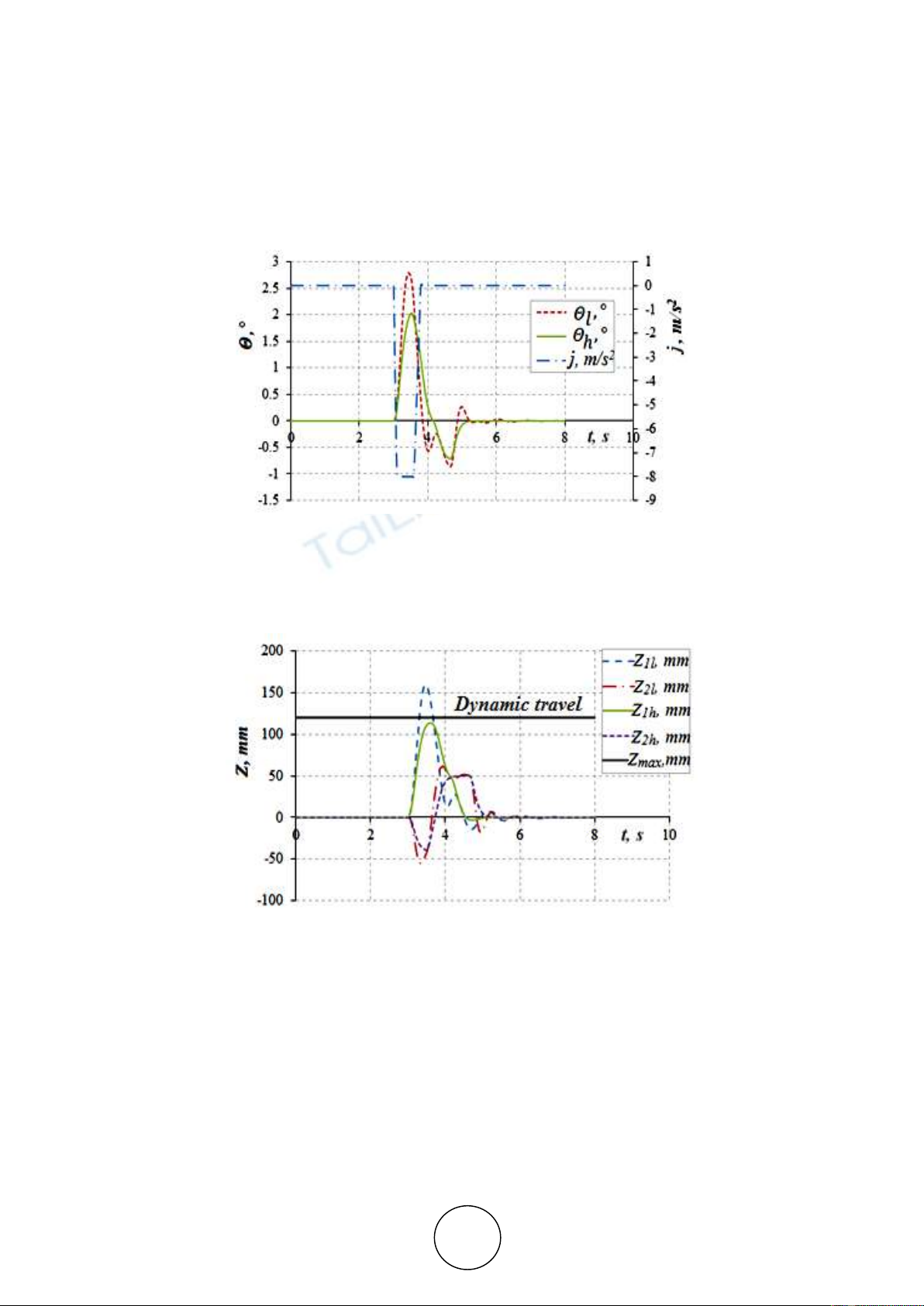
The simulation results of a pith angle and suspension deflection with two different damping
coefficients are shown in Fig. 5 and Fig 6.
Figure 5 Effect of the shock absorber damping ratio (β) on the pitch angle θ when the truck brakes on
the railway crossing with maximum acceleration j=8 m/s2. Subscribe l when βlow, h when βhigh
In the figures 5 and 6 can be seen how increasing the damping reduce the truck pitch angle
and eliminate the suspension jounce.
Figure 6 Effect of the shock absorber damping ratio (β) on the front z1 and rear z2 suspension
deflection when the truck brakes on the railway crossing with maximum acceleration j=8 m/s2.
Subscribe l when βlow, h when βhigh. The black line shows the maximum of the dynamic suspension
travel deflection
The principal diagram of a possible control system for reducing the pitch angle and
suspension jounce is shown in Fig. 7. The controller receives signals from the displacement
sensors and generates control signals to the shock absorbers.