
1. PH N M ĐUẦ Ở Ầ
1.1. LÝ DO CH N Đ TÀI:Ọ Ề
Đ đáp ng đc yêu c u c a s nghi p giáo d c và nhu c u h c t p c aể ứ ượ ầ ủ ự ệ ụ ầ ọ ậ ủ
h c sinh, trong quá trình gi ng d y m i giáo viên ph i bi t ch t l c nh ng n iọ ả ạ ỗ ả ế ắ ọ ữ ộ
dung ki n th c c b n m t cách rõ ràng, ng n g n và đy đ, ph i đi t d đnế ứ ơ ả ộ ắ ọ ầ ủ ả ừ ễ ế
khó, t đn gi n đn ph c t p, t c th đn tr u t ng giúp h c sinh có thừ ơ ả ế ứ ạ ừ ụ ể ế ừ ượ ọ ể
n m đc n i dung chính trong bài h c, đng th i có th g i m , đt v n đắ ượ ộ ọ ồ ờ ể ợ ở ặ ấ ề
đ h c sinh phát tri n t duy cũng nh kĩ năng phân tích, trình bày bài gi i m tể ọ ể ư ư ả ộ
cách ch t ch , logíc, có h th ng. Trong nh ng năm g n đây, vi c đi m iặ ẽ ệ ố ữ ầ ệ ổ ớ
ph ng pháp d y h c là v n đ c p bách và c n thi t, nươ ạ ọ ấ ề ấ ầ ế h m hình thành cho h cằ ọ
sinh thói quen t duy tích c c, đc l p sáng t o, nâng cao năng l c phát hi n vàư ự ộ ậ ạ ự ệ
gi i quy t v n đ, rèn luy n cho các em năng l c v n d ng ki n th c vào th cả ế ấ ề ệ ự ậ ụ ế ứ ự
ti n. Chính vì v y, m i giáo viên đng l p ph i có m t ph ng pháp truy n đtễ ậ ỗ ứ ớ ả ộ ươ ề ạ
ki n th c phù h p, có kh năng h th ng, phân lo i và ch n l a các d ng bàiế ứ ợ ả ệ ố ạ ọ ự ạ
t p phong phú, đáp ng đc yêu c u t i thi u c a ng i h c, tác đng đnậ ứ ượ ầ ố ể ủ ườ ọ ộ ế
tình c m, đem l i ni m tin và s h ng thú trong h c t p c a h c sinh.ả ạ ề ự ứ ọ ậ ủ ọ
Qua th c t gi ng d y nhi u năm, cũng nh qua vi c theo dõi k t qu cácự ế ả ạ ề ư ệ ế ả
bài ki m tra, bài thi c a h c sinh, tôi nh n th y v n còn nhi u h c sinh m cể ủ ọ ậ ấ ẫ ề ọ ắ
ph i các sai l m không đáng có khi gi i toán ch a căn th c b c hai còn nhi u saiả ầ ả ứ ứ ậ ề
sót, r p khuôn máy móc ho c ch a làm đc do ch a n m ch c các ph ngậ ặ ư ượ ư ắ ắ ươ
pháp gi i, v n d ng k năng bi n đi ch a linh ho t vào t ng d ng toán. ả ậ ụ ỹ ế ổ ư ạ ừ ạ
Trong khi đó, k thi h c k 1 và các k thi cu i c p. Nôi dung đê thiở ỳ ọ ỳ ỳ ố ấ $
th ng r i vao kiên th c c ban không thê thiêu đo la ch ng căn th c bâc hai ươ ơ ư ơ % % ươ ư $
cho d i dang rut gon biêu th c, th c hiên phép tinh căn ho c gi i ph ng trình. ươ $ $ % ư ư$ $ ặ ả ươ
Đ tháo g và gi i quy t nh ng khó khăn, v ng m c trong h c t pể ỡ ả ế ữ ướ ắ ọ ậ
đng th i nh m phát tri n năng l c t duy cho h c sinh, tôi nh n th y vi c rènồ ờ ằ ể ự ư ọ ậ ấ ệ
luy n k năng gi i toán có ch a căn th c b c hai cho h c sinh là r t c n thi t.ệ ỹ ả ứ ứ ậ ọ ấ ầ ế
V i các lí do trên, tôi xin đc trình bày m t s kinh nghi m đc rút ra trongớ ượ ộ ố ệ ượ
quá trình gi ng d y v i tên đ tài: ả ạ ớ ề “Rèn luy n kĩ năng s d ng h ng đngệ ử ụ ằ ẳ
th c đ gi i m t s d ng toán có ch a căn th c b c hai”.ứ ể ả ộ ố ạ ứ ứ ậ Đ tài này nh mề ằ
giúp h c sinh l p 9, cac hoc sinh kha, gioi môn toan va đc th c hiên trong cac ọ ớ $ % ươ$ ư$ $
gi luyên tâp, ôn tâp, ôn thi vao l p 10 vê giai bai tâp rut gon biêu th c co ch a ơ $ $ $ ơ % $ $ % ư ư
căn th c, th c hiên phep tinh và gi i ph ng trình ch a căn b c hai. ư ư$ $ ả ươ ứ ậ
1.2. ĐI M M I C A Đ TÀIỂ Ớ Ủ Ề :
Đ tài này đã có m t s sách tham kh o cho h c sinh THCS ề ộ ố ả ọ nh ng ch aư ư
t ng h p đc và ch a v n trong nhi u d ng toán, ng d ng các bài toán khácổ ợ ượ ư ậ ề ạ ứ ụ
nhau.
1

- đ tài này tôi đã xây d ng m t cách t ng quát, đy đ, chi ti t cho t tỞ ề ự ộ ổ ầ ủ ế ấ
c các tr ng h p ả ườ ợ vê áp d ng h ng đng th c đ giai bai tâp rut gon biêu th c ụ ằ ẳ ứ ể % $ $ % ư
co ch a căn th c b c hai, th c hiên phep tinh và gi i ph ng trình ch a căn b c ư ư ậ ư$ $ ả ươ ứ ậ
hai.
- Có h th ng bài t p áp d ng đ HS hi u đy đ t d đn khó, cácệ ố ậ ụ ể ể ầ ủ ừ ể ế
tr ng h p áp d ng h ng đng th c khác nhau đ làm r các d ng toán này,ườ ợ ụ ằ ẳ ứ ể ỏ ạ
đng th i có nh ng bài t p nâng cao đ h c sinh phát tri n t duy sáng t o c aồ ờ ữ ậ ể ọ ể ư ạ ủ
b n thân.ả
- Xây d ng cho h c sinh ni m tin trong h c t p, ch ng t t ng ng i khó,ự ọ ề ọ ậ ố ư ưở ạ
s toán, giúp các em hăng say h c t p, h ng thú tìm tòi cái hay cái m i trong toánợ ọ ậ ứ ớ
h c. ọ
Đ tài cũng là m t tài li u tham kh o cho các giáo viên trong quá trình đcề ộ ệ ả ọ
và nghiên c u tài li u, cũng nh gi ng d y. Ngoài m c đích trên đ tài có thứ ệ ư ả ạ ụ ề ể
coi nh m t gi i pháp góp ph n th c hi n đi m i ph ng pháp d y h c theoư ộ ả ầ ự ệ ổ ớ ươ ạ ọ
h ng phát huy năng l c c a h c sinh và đi m i ki m tra đánh giá tr ngướ ự ủ ọ ổ ớ ể ở ườ
THCS.
1.3. PH M VI ÁP D NG C A Đ TÀIẠ Ụ Ủ Ề :
Đ tài đc áp d ng đ gi ng d y cho h u h t các đi t ng h c sinh h cề ượ ụ ể ả ạ ầ ế ố ượ ọ ọ
l p 9, cho đi tuy n h c sinh gi i c p tr ng, c p huy n b c THCS và là tàiớ ộ ể ọ ỏ ấ ườ ấ ệ ậ
li u cho h c sinh h c lên THPT v a là tài li u tham kh o cho giáo viên tham giaệ ọ ọ ừ ệ ả
gi ng d y môn toán THCS và b i d ng HSG toán 9.ả ạ ồ ưỡ
Đ tài ch nghiên c u đn d ng bài toán v s d ng h ng đng th c đề ỉ ứ ế ạ ề ử ụ ằ ẳ ứ ể
giai bai tâp rut gon biêu th c co ch a căn th c, th c hiên phep tinh và gi i % $ $ % ư ư ư ư$ $ ả
ph ng trình ch a căn b c hai.ươ ứ ậ
2
2. PH N N I DUNG Ầ Ộ
2.1.TH C TR NG KHI CH A ÁP D NG Đ TÀIỰ Ạ Ư Ụ Ề :
2.1.1. S li u th ng kê: ố ệ ố
Đ th c hi n đ tài tôi ti n hành kh o sát ch t l ng h c sinh d ng bàiể ự ệ ề ế ả ấ ượ ọ ạ
t p này tr c khi tri n khai kinh nghi m thu đc nh sau:ậ ướ ể ệ ượ ư
K t qu bài ki m tra s 1 ế ả ể ố ( Tr c khi tri n khai kinh nghi m.)ướ ể ệ
L pớSĩ sốGi iỏKháTB Y u – kémế
SL % SL % SL % SL %
9135 4 11,4 8 22,9 12 34,3 11 31,4
9234 4 11,7 7 20,6 13 38,3 10 29,4
2.1.2. Tình hình tr c khi th c hi n các gi i pháp c a đ tài: ướ ự ệ ả ủ ề
Đi v i h c sinh tr ng THCS n i tôi đang công tác ph n l n các emố ớ ọ ườ ơ ầ ớ đcượ
h c đy đ các ki n th c c b n, có ph n m r ng và nâng cao nhi u. Song khiọ ầ ủ ế ứ ơ ả ầ ở ộ ề
g p m t bài toán, h c sinh v n b lúng túng trong đnh h ng ph ng pháp gi i,ặ ộ ọ ẫ ị ị ướ ươ ả
ch a bi t v n d ng ho c v n d ng ch a linh ho t, sáng t o các ki n th c cư ế ậ ụ ặ ậ ụ ư ạ ạ ế ứ ơ
b n đã h c. Nhi u h c sinh ch bi t v n d ng t ng b c gi i, t ng ph n c aả ọ ề ọ ỉ ế ậ ụ ừ ướ ả ừ ầ ủ
quy t c, công th c mà th y, cô đã h ng d n. ắ ứ ầ ướ ẫ Đi u này h n ch r t l n đnề ạ ế ấ ớ ế
vi c phát huy tính tích c c và đc l p nh n th c khi gi i toán c a h c sinh, d nệ ự ộ ậ ậ ứ ả ủ ọ ẫ
đn các em không ham h c toán và không t tin khi gi i toán, lúng túng trong líế ọ ự ả
lu n và trình bày.ậ
2.1.3. Nguyên nhân d n đn tình hình trên:ẫ ế
* V giáo viên:ề
- Vi c truy n t i ki n th c c a căn th c b c hai cho h c sinh đang còn h nệ ề ả ế ứ ủ ứ ậ ọ ạ
ch .ế
3

- Ch a hình thành đc cho h c sinh k năng gi i, mô hình gi i, cách gi iư ượ ọ ỹ ả ả ả
ng v i t ng tr ng h p, t ng bài t p v n d ng các h ng đng th c đã h cứ ớ ừ ườ ợ ừ ậ ậ ụ ằ ẳ ứ ọ
d i d ng bi u th c ch a d u căn l p 9.ướ ạ ể ứ ứ ấ ở ớ
- K năng rèn luy n cho h c sinh t duy, đnh h ng tr c m t bài toán vàỹ ệ ọ ư ị ướ ướ ộ
kh năng phân tích đ bài ch a đc chú tr ng.ả ề ư ượ ọ
* V h c sinh:ề ọ
- Đng c thái đ h c t p c a nhi u h c sinh ch a th t t t. H c sinh v nộ ơ ộ ọ ậ ủ ề ọ ư ậ ố ọ ẫ
quen v i l i h c th đng, ch a s n sàng tham gia m t cách tích c c, ch đngớ ố ọ ụ ộ ư ẵ ộ ự ủ ộ
vào các n i dung h c t p.ộ ọ ậ
- Ch a n m v ng các h ng đng th c đã h c l p 8 nên không chu n bư ắ ữ ằ ẳ ứ ọ ở ớ ẩ ị
t t tâm th cho gi h c Toán. ố ế ờ ọ
- K năng v n d ng các h ng đng th c đã h c d i d ng bi u th c ch aỹ ậ ụ ằ ẳ ứ ọ ướ ạ ể ứ ứ
d u căn th c l p 9 ch a thành th o. ấ ứ ở ớ ư ạ
- H c sinh ch a hình thành đc mô hình gi i toán, các b c đ gi i m tọ ư ượ ả ướ ể ả ộ
bài toán.
- K năng phân tích đ bài và đnh h ng đc cách làm c a m t bài, m tỹ ề ị ướ ượ ủ ộ ộ
d ng c a h c sinh còn khiêm t n.ạ ủ ọ ố
2.2. CÁC GI I PHÁP:Ả
2.2.1. Cho h c sinh n m v ng b y h ng đng th c đã h c l p 8ọ ắ ữ ả ằ ẳ ứ ọ ở ớ
Đê khăc phuc vân đê đa nêu trên, ta cân cho hoc sinh n m ch c bay hăng % $ ơ% $ ắ ắ %
đăng th c đa hoc l p 8. % ư $ ơ% ơ
1) Binh ph ng môt tông : (a + b)ươ $ % 2 = a2 + 2ab + b2
2) Binh ph ng môt hiêu : (a – b)ươ $ $ 2 = a2 – 2ab + b2
3) Hiêu hai binh ph ng :$ ươ a2 – b2 = (a + b).(a – b)
4) Lâp ph ng môt tông :$ ươ $ % (a + b)3 = a3 + 3a2b + 3ab2 + b3
5) Lâp ph ng môt hiêu : (a – b)$ ươ $ $ 3 = a3 – 3a2b + 3ab2 – b3
6) Tông hai lâp ph ng :% $ ươ a3 + b3 = (a + b).(a2 – ab + b2)
7) Hiêu hai lâp ph ng :$ $ ươ a3 – b3 = ( a – b).(a2 + ab + b2)
Biêt vân dung no đê đa ra nh ng hăng đăng th c đang nh l p 9 (theo $ $ % ư ư % ư ơ ơ% ơ
th t ) viêt d i dang co dâu căn. (v i ư ư$ ươ $ ớ a ; b > 0)
4
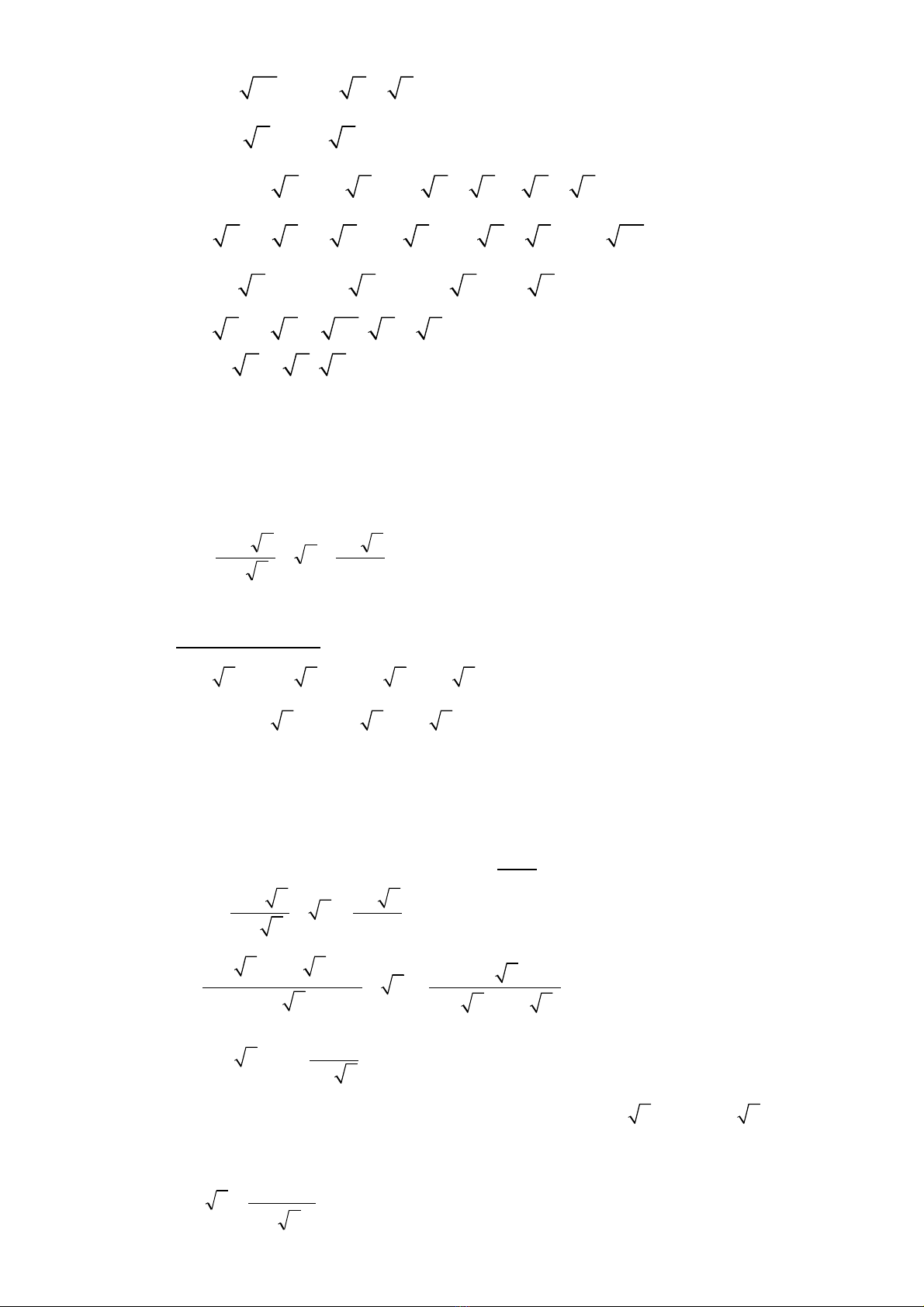
( )
( )
( ) ( ) ( ) ( )
( ) ( ) ( )
( )
( ) ( )
2
2
2 2
3 3
3
3
1) 2
2) 2 1 1
3) .
4) ( ).
5)1 1 (1 ). 1
6) ( )
7) ( 1)
a ab b a b
a a a
a b a b a b a b
a a b b a b a b a ab b
a a a a a a
a b b a ab a b
a a a a
+ + = +
− + = −
− = − = + −
+ = + = + − +
− = − = − + +
+ = +
+ = +
2.2.2. S d ng h ng đng th c đ rút g n bi u th c có ch a căn th c b cử ụ ằ ẳ ứ ể ọ ể ứ ứ ứ ậ
hai:
D ng 1: Ch ng minh đng th cạ ứ ẳ ứ
Bài 1: Ch ng minh cac đăng th c sau: ư % ư
a)
1
1
1
1
12
a
a
a
a
aa
Nhân xet đê bai: Bai toan cho gôm co cac h ng đăng th c sau : ằ % ư
( ) ( ) ( )
( ) ( ) ( )
3
3
2
2
1 1 1 . 1
1 1 1 . 1
a a a a a a
a a a a
− = − = − + +
− = − = − +
t ng t hăng đăng th c sô 3; 7 l p 8. Ap dung vao bai toan, ta biên đôi vê ươ ư$ % ư ơ $ %
trai:
Giai%
( ) ( ) ( ) ( )
( )
2
2
2
1 1
1
1
1 . 1 1
.
11 . 1
1
1 2 . 1
a a a
VT a a
a
a a a a
a
aa a
a a a
� �� �
− −
= +
� �� �
� �� �
−
−
� �� �
� �� �
− + + −
� �� �
= +
� �� �
−+ −
� �� �
� �
= + + � �
+
� �
Đên đây ta lai thây xuât hiên h ng đng th c: $ $ ằ ẳ ứ
( ) ( )
2
1 2 1a a a+ + = +
t ng tươ ư$
h ng đng th c sô 1 l p 8. Tiêp tuc biên đôi ta đc kêt qua: ằ ẳ ứ ơ $ % ươ$ %
VP
a
aVT
1
1
1
.1 2
2
5
(v i aớ
0; a
1)
















