Ôn Tập chương I
Gi¸o Viªn Phạm Văn Quý - 1 -
THEÅ TÍCH KHOÁI ÑA DIEÄN
1 Tính theå tích cuûa hình hoäp chöõ nhaät coù chieàu roäng baèng 1 , chieàu daøi baèng 3 vaø ñöôøng cheùo
cuûa hình hoäp hôïp vôùi maët ñaùy moät goùc 30 .
ĐS: V = 2 (đvtt)
2 Cho hình hoäp vôùi saùu maët ñeàu laø hình thoi caïnh a , goùc nhoïn baèng 60 . Tính theå tích cuûa hình hoäp.
ĐS:
3
a2
V 2
(đvtt)
3 Ñaùy cuûa moät hình hoäp laø moät hình thoi coù caïnh baèng 6cm vaø goùc nhoïn baèng 45 , caïnh beân cuûa hình
hoäp daøi 10cm vaø taïo vôùi maët phaúng ñaùy moät goùc 45 .Tính theå tích cuûa khoái hoäp .
ĐS: V =180 (đvtt)
฀
23
ABCD
4 Cho hình hoäp ñöùng ABCD.A'B'C'D' coù ABCD laø hình thoi caïnh a vaø BAD 60 , AB' hôïp vôùi ñaùy
(ABCD) moät goùc . Tính theå tích cuûa hình hoäp .
a 3 3
ñs: V = S .BB' .atan a tan
22
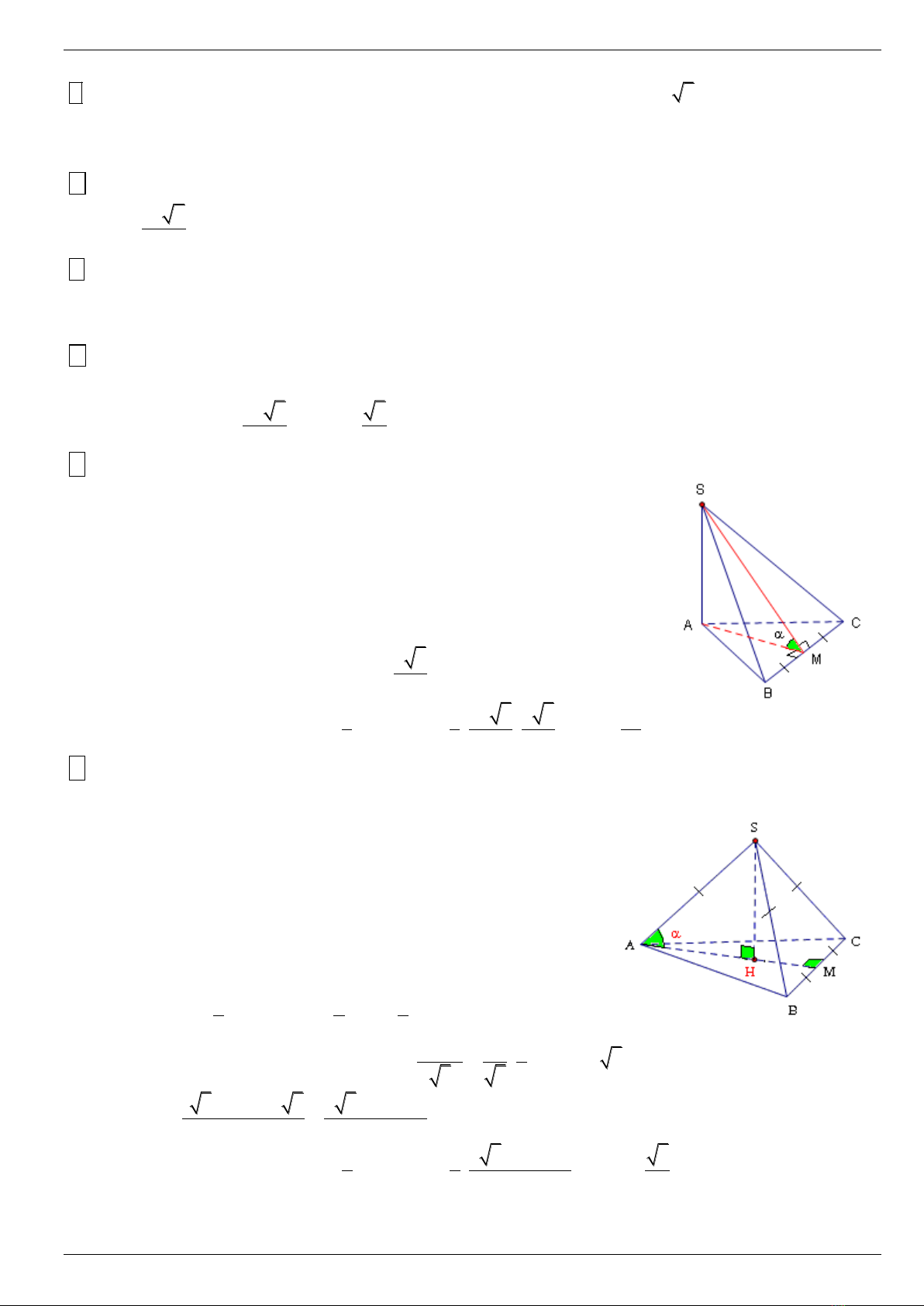
5 Cho khoái choùp S.ABC coù ñaùy ABC laø tam giaùc ñeàu caïnh a , SA (ABC) . Maët beân (SBC) taïo vôùi
maët phaúng ñaùy moät goùc . Tính theå tích khoái choùp .
Giaûi
Goïi M laø trung ñieåm BC , vì
฀
฀
ñl3ñ
(ABC)
ABC ñeàu neân AM BC (1)
Do AM = hc SM,AM BC SM BC (2)
Maët khaùc : (SBC) (ABC) = BC (3)
Töø (1),(2),(3) ((SBC);(ABC)) = SMA

23
ABC
1 1 a 3 a 3 a
Vaäy theå tích hình choùp laø V= .S .SA . . .tan tan
3 3 4 2 8
6 Cho khoái choùp tam giaùc ñeàu coù caïnh beân baèng a vaø caùc caïnh beân taïo vôùi maët phaúng ñaùy moät goùc .
Tính theå tích cuûa khoái choùp .
Giaûi
Goïi khoái choùp tam giaùc ñeàu ñaõ cho laø S.
฀
฀
฀
(ABC) (ABCD)
ABC neân SA = SB = SC .
Keû SH (ABC) taïi H thì H laø taâm cuûa tam giaùc ñeàu ABC .
Goïi M laø trung ñieåm BC .
Vì H = hc S AH = hc AS (SA;(ABC)) SAH
SHA vuoâng taïi H coù SAH neân AH = S
2 2 2
ABC
A.cos a.cos .
SH = AH.tan acos .tan asin .
2 3 3
Maët khaùc : AH = AM AM .AH acos
3 2 2 2.AM 2 3
Maø ABC ñeàu coù ñöôøng cao AM neân AB = . acos 3acos
2
33
( 3acos ) . 3 3 3a cos
S 44
Vaäy theå tích

22 32
ABC
1 1 3 3a cos 3
cuûa khoái choùp laø V = .S .SH . .asin a cos sin
3 3 4 4
Ôn tập chương I
- 2 -
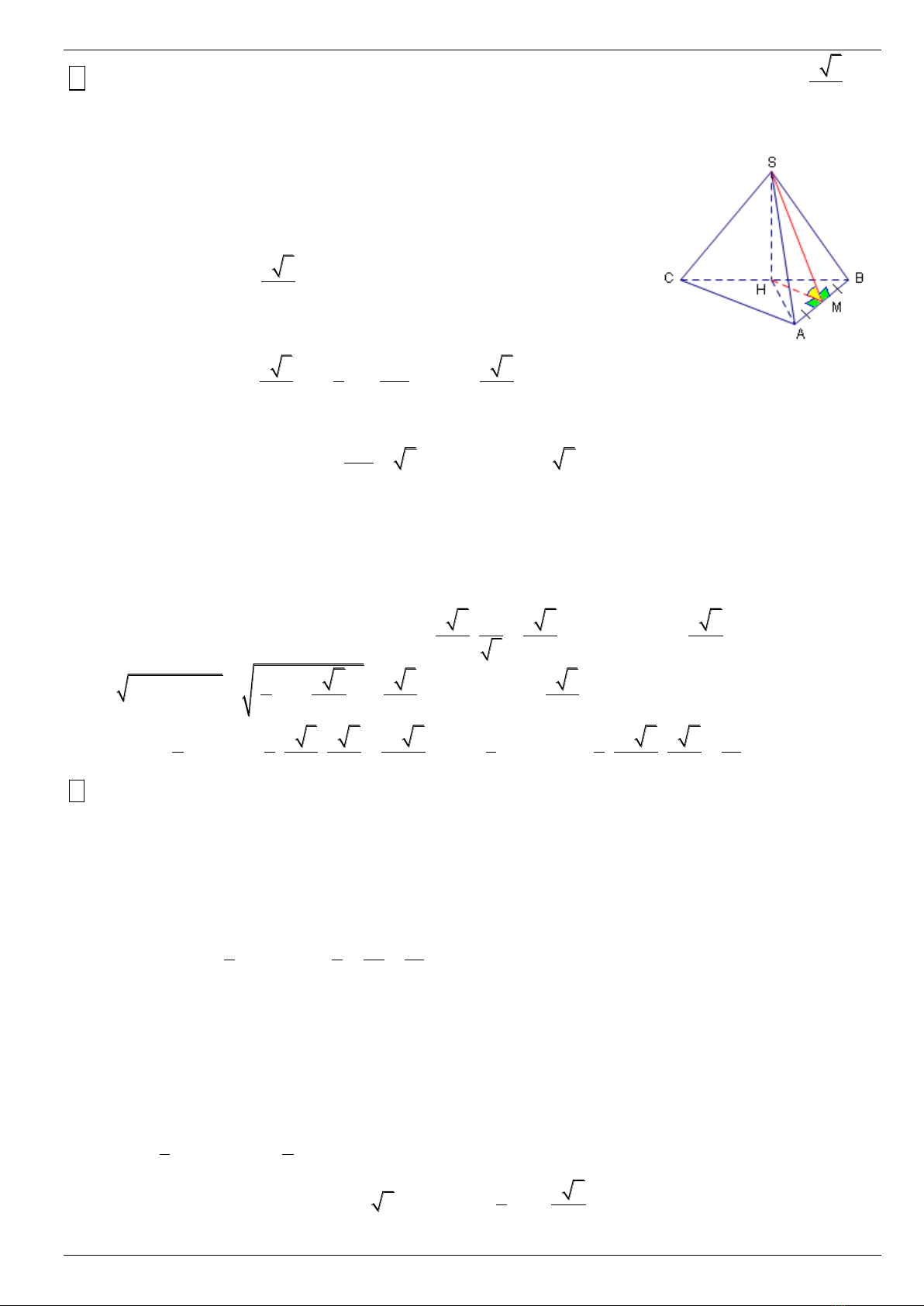
a3
7 Khoái choùp tam giaùc S.ABC coù ñaùy ABC laø tam giaùc vuoâng taïi A , BC = a ; SA = SB = SC = vaø
2
maët beân SAB hôïp vôùi ñaùy moät goùc 60
a) Tính khoaûng caùch töø S ñeán maët phaúng (ABC) .
b
) Tính goùc giöõa ñöôøng thaúng SA vaø maët phaúng (ABC) .
c) Tính theå tích cuûa khoái choùp S.ABC
Giaûi
a) Döïng SH (ABC)
a3
Ta coù : SA = SB = SC = HA = HB = HC
2
H laø taâm cuûa ñöôøng troøn ngoaïi
฀
฀
฀฀
2
2 2 2 2 2
(ABC) (ABC)
tieáp ABC
Vì ABC vuoâng taïi A neân H laø trung ñieåm BC .
a 3 a 3a a 2
Do SH SB HB ( ) ( ) SH
2 2 4 2
b) Do SH (ABC) H hc S AH hc AS (SA;(ABC)) SAH 60
SH
SAH vuoâng taïi H neân tanSAH 2 SAH
AH
acrtan 2
c) Goïi M laø trung ñieåm AB
฀
฀
(ABC) (ABC)
ñlí 3 ñ
2
Do SH (ABC) H hc S MH hc MS maø HM AB (1) vì HM // AC
MS AB (2)
Töø (1),(2) (SA;(ABC)) SAH 60
a 2 1 a 6 a 6
SHM vuoâng taïi H , ta coù : MH = SH.tan60 . AC 2MH ,
2 6 3
3
MB HB MH


2 2 2
a a 6 a 3 a 3
( ) ( ) AB 2MB
2 6 6 3
2 2 3
ABC ABC
1 1 a 3 a 6 a 2 1 1 a 2 a 2 a
S .AB.AC . . V .S .SH . .
2 2 3 3 6 3 2 6 2 12
8 Cho khoái choùp S.ABC coù ñöôøng cao SA = a, ñaùy laø tam giaùc vuoâng caân AB = BC = a . Goïi B' laø
trung ñieåm cuûa SB , C' laø chaân ñöôøng cao haï töø A cuûa SAC .
a) Tính theå tích khoái choùp
23
S.ABC ABC
S.ABC .
b) Chöùng minh raèng SC vuoâng goùc vôùi mp(AB'C') .
c) Tính theå tích khoái choùp S.AB'C' .
HD
1 1 a a
a) Ta coù : V .S .SA .a.
3 3 2 6
b) Ta coù :
BC AB
BC (SAB) BC AB' (1)
BC SA
SAB c

฀
S.AB'C' AB'C'
aân taïi A neân SB AB' (2)
Töø (1),(2) suy ra AB' (SBC) AB' SC . Maët khaùc : AC' SC neân SC (AB'C')
c) Ta coù
11
V .SC'.S .SC'.AB'.B'C'
36
SAB vuoâng caân taïi A, ta coù : SB = a 2,AB' 
1 a 2
SB' SB
22
Ôn tập chương I
- 3 -
฀2 2 2 2 2 2 2
22
2
3
SAC vuoâng caân taïi A, ta coù : SC = SA AC SA AB BC 3a SC a 3
SA a a 3
SA SC'.SC SC' SC 3
a3
a2
B'C' SB' 6 a 6
2
B'C'
BC SC 6 6
a3
1 a 3 a 2 a 6 a
Vaäy V = . . .
6 3 2 6 36
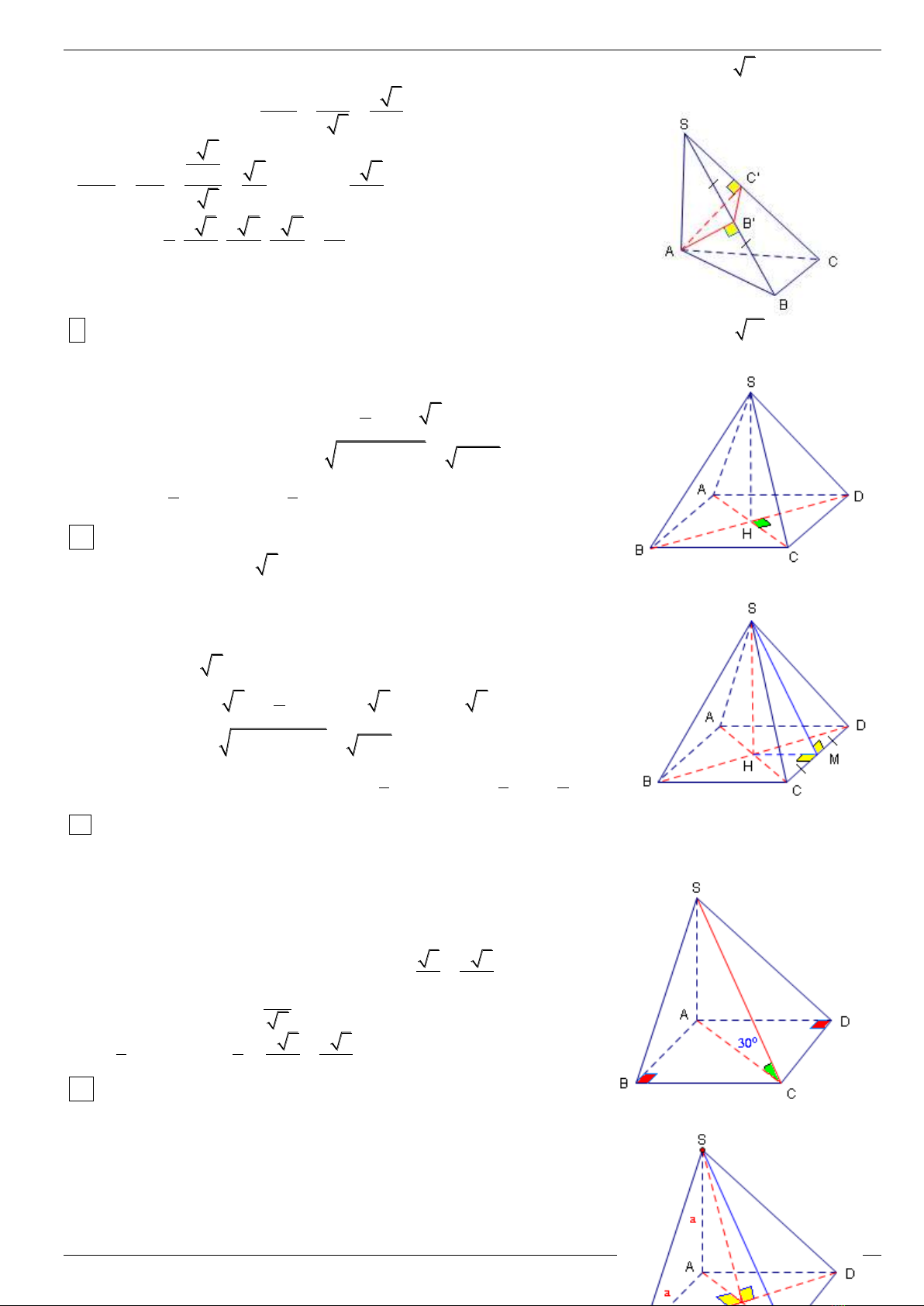
9 Tính theå tích cuûa khoái choùp töù giaùc ñeàu , maët ñaùy coù caïnh baèng 2 , caïnh beân baèng 11 .
Giaûi
Goïi hình choùp töù giaùc ñeàu laø S.ABCD vaø H laø taâm cuûa maët ñaùy ABCD .
Ta coù : SH (AB
22
2
ABCD
1
CD) taïi H vaø AH = AC 2
2
Vì SHD vuoâng taïi H neân SH = SD HD 11 2 3
11
Vaäy V = .S .SH .2 .3 4
33

10 Cho hình choùp töù giaùc ñeàu coù dieän tích ñaùy baèng 4 vaø dieän tích
cuûa moät maët beân baèng 2 . Tính theå tích cuûa hình choùp ñoù .
SCD
22
Giaûi
Goïi hình choùp ñaõ cho laø S.ABCD , H laø taâm cuûa maët
ñaùy ABCD vaø M laø trung ñieåm cuûa CD.
Caïnh ñaùy : a = 4 2
1
Maët beân : S 2 .CD.SM 2 SM 2
2
Chieàu cao : SH = SM HM 2 1 1
฀
฀
฀
ABCD
1 1 4
Vaäy theå tích cuûa khoái choùp laø V = .S .SH .4.1
3 3 3

11 Cho hình choùp S.ABCD coù ñaùy ABCD laø hình vuoâng vaø ñöôøng cheùo AC = 2 . Bieát SA (ABCD) vaø
caïnh beân SC taïo vôùi maët phaúng ñaùy moät goùc 30 . Tính theå
tích cuûa khoái choùp S.ABCD .
G
฀
฀
(ABCD) (ABCD)
22
ABCD
ABCD
iaûi
Vì SA (ABCD) A = hc S AC = hc SC
(SC;(ABCD)) SCA 30
3 2 3
SAC vuoâng taïi A neân SA = AC.tan30 2. 23
AC
S AB ( ) 2
2
1 1 2 3 4 3
V = .S .SA .2.
3 3 3 9

฀
฀
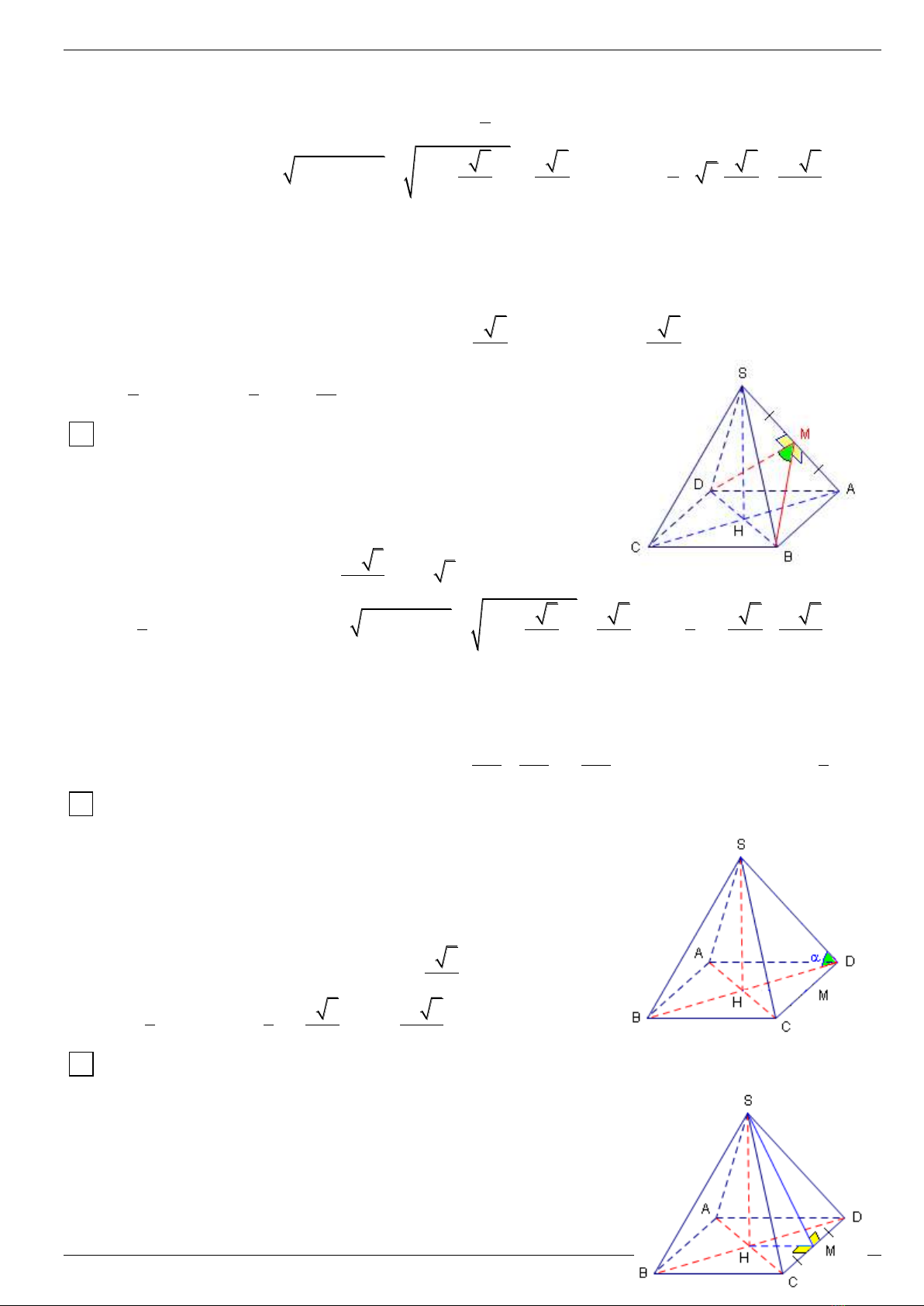
12 Cho hình choùp S.ABCD coù ñaùy ABCD laø hình vuoâng caïnh ,
caïnh SA vuoâng goùc vôùi maët ñaùy vaø SA = AB = a .
a) Tính dieän tích SBD theo a .
b) Chöùng minh raèng : BD SC .
c) Tính goùc taïo
bôûi SC vaø maët phaúng (SBD) .
d) Tính theå tích khoái choùp S.ABCD .
Ôn tập chương I
- 4 -
BCD
2
2 2 2 2 BCD
Giaûi
a) Ta coù : SA (ABCD) . Goïi H laø taâm cuûa hình vuoâng ABCD .
1
Noái S vaø H thì SH BD (Ñlí 3 ñ ) neân S .BD.SH
2
a 2 a 6 1 a 6 a 3
ASH vuoâng taïi A : SH SA AH a ( ) = S .a 2.
2 2 2 2 2
฀
฀
฀
฀
(SBD)
BD AC ( hai ñöôøng cheùo hình vuoâng)
b) Ta coù : BD (SAC) maø SC (SAC) neân BD SC
BD SA ( vì SA (ABCD))
c) Keû CK SH thì CK BD ( do BD (SAC)) CK (SBD) K= hc C (SC;(SBD)) = CSH
AÙp duïng ñlí

฀ ฀ ฀
2 2 2
3
2
ABCD
haøm soá cosin trong SCH ta ñöôïc :
2 2 2 2
HC SH SC 2SH.SC.cosHSC cosHSC HSC acrcos .
33
1 1 a
d) V = .S .SA .a .a
3 3 3

12 (ÑHSPTpHCM-D2000) Cho hình choùp töù giaùc ñeàu S.ABCD coù
ñaùy ABCD laø hình vuoâng caïnh a vaø SA = SB = SC = SD = a .
a) Tính dieän tích toaøn phaàn vaø theå tích hình choùp S.ABCD theo a .
b) Tính cosin cuûa goùc nhò dieän (SBA,SAD) .
2
22
tp ABCD SAB
3
2 2 2 2 2
ABCD
HD
a3
a) S S 4.S a 4. (1 3)a .
4
1 a 2 a 2 1 a 2 a 2
V = .S .SH , ta coù : SH = SA HA a ( ) V= .a . =
3 2 2 3 2 6
฀
฀
฀
b) Goïi M laø trung ñieåm cuûa SA , ta coù : BM SA vaø DM SA = BMD laø goùc phaúng cuûa nhò dieän
(SAB,SAD) .
฀ ฀ ฀
2 2 2
2 2 2 2
AÙp duïng ñlí haøm soá cosin trong BMD ta ñöôïc :
3a 3a 3a 1
BD MB MD 2MB.MD.cosBMD 2a 2. .cosBMD cosBMD
4 4 4 3
13 Cho hình choùp töù giaùc ñeàu coù caïnh ñaùy baèng a vaø caùc caïnh beân hôïp vôùi ñaùy moät goùc . Tính theå
tích cuûa khoái choùp töù giaùc ñeàu .
HD
Goïi hình choùp töù giaùc ñeàu laø S.ABCD vaø
฀
฀ ฀ ฀
3
2
ABCD
maët ñaùy laø hình
vuoâng ABCD coù taâm H .
Keû ñöôøng cao SH , ta coù SAH SBH SBH SBH
a2
Xeùt SAH vuoâng taïi H neân SH = AH .tan tan
2
1 1 a 2 a 2
Vaäy V = .S .SH .a . tan tan
3 3 2 6

14 Cho hình choùp töù giaùc ñeàu coù caïnh ñaùy baèng a vaø caùc maët beân hôïp vôùi ñaùy moät goùc . Tính theå
tích cuûa khoái choùp töù giaùc ñeàu .
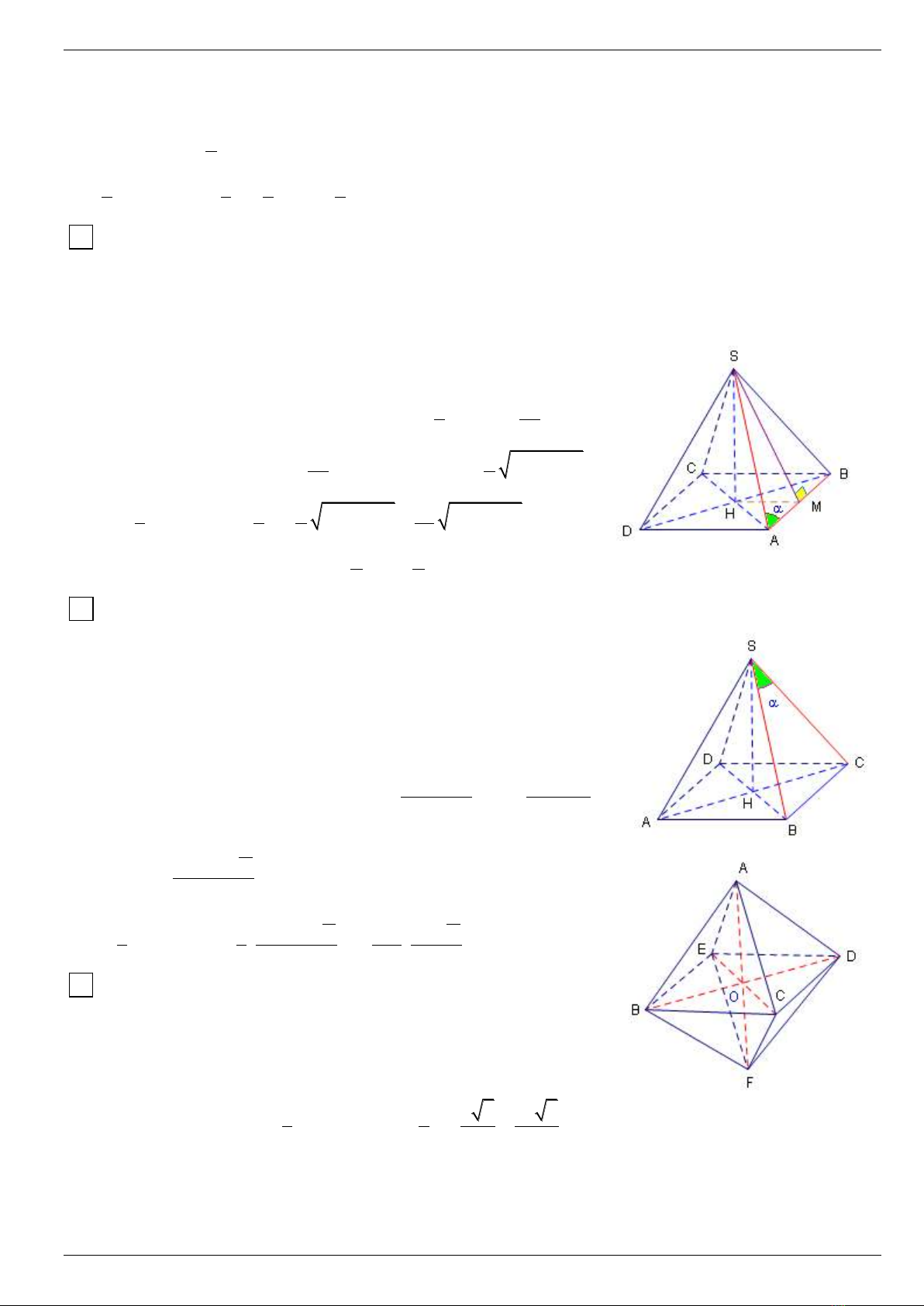
Ôn tập chương I
- 5 -
฀
23
ABCD
HD
Goïi hình choùp ñaõ cho laø S.ABCD , H laø taâm cuûa maët
ñaùy ABCD vaø M laø trung ñieåm cuûa CD thì SMH
a
SH HM.tan tan
2
1 1 a 1
V .S .SH .a . tan a tan
3 3 2 6

฀
15 (YHN-2000) Cho hình choùp töù giaùc ñeàu S.ABCD coù ñoä daøi caïnh
ñaùy AB = a vaø SAB . Tính theå tích khoái choùp S.ABCD theo a vaø .
HD
Goïi H laø taâm cuûa ñaùy ABCD vaø M laø trung ñieåm AB
ñlí 3 ñ
(ABCD) (ABCD) 2
2 2 2 2
22
.
Khi ñoù : SH (ABCD) vaø HM AB .
Vì H = hc S HM= hc SM SM AB
aa
SMA vuoâng taïi M neân SH SM HM ( tan )
24
aa
(tan 1) SH ta
42


2
3
2 2 2
ABCD
2
n1
1 1 a a
Vaäy V= .S .SH .a . tan 1 tan 1
3 3 2 6
Vôùi ñieàu kieän tan 1 0 42


16 Cho hình choùp töù giaùc ñeàu S.ABCD coù ñöôøng cao baèng a vaø caùc maët beân laø tam giaùc caân coù goùc ôû
ñænh baèng .
฀
2 2 2 2 2 2
2 2 2
HD
Goïi BSH = . AÙp duïng ñl cosin vaøo SBD vaø SBC :
BD 2SB (1 cos2 ) BC 2SB .sin
sin 1 cos
BC 2SB (1 cos ) cos cos
฀
2
2 2 2 2 2 2
ABCD 2
1 cos 1 cos
S BC 2HB 2a tan 2a . 2a . cos
cos
฀
22
2 2 2
3
ABCD
4a sin 2
S = cos
4a sin sin
1 1 4a
22
V = .S .SH . .a .
3 3 cos 3 cos



฀
17 Tính theå tích cuûa khoái taùm maët ñeàu coù caïnh baèng a .
Giaûi
Goïi khoái taùm maët ñeàu ñaõ cho laø ABCDE vaø O laø taâm cuûa hình
vuoâng BCDE coù caïnh baèng a .
Vì maët BCDE chia khoái taùm maë
3
2
ABCDEF ABCDE BCDE
t ñeàu thaønh hai phaàn baèng nhau neân :
1 1 a 2 a 2
V = 2.V 2. .S .AO 2. .a .
3 3 2 3