
LuyÖn thi ®¹i häc
CHINH PHôC
CHUY£N §Ò:
hÌNh@KhÔNG@GIAN
tHÇY HIÕU LIVE
To¸n häcLuyÖn thi ®¹i häcTo¸n häc
Trung t©m luyÖn thi
HäC VI£N:
T¤I QUYÕT T¢M THI §ËU §¹I HäC
To¸nhäc

LUYỆN THI ĐẠI HỌC – ĐẶNG QUANG HIẾU – 0988 593 390 – FACEBOOK: HIẾU LIVE
Trung Tâm Olympia – Uy Tín – Chất Lượng – Tận Tâm
Page 0
MỤC LỤC HÌNH KHÔNG GIAN
STT
Kiến thức
Trang
1.
Một số công thức giải tam giác và công thức tính diện tích
1
2.
Lý thuyết về quan hệ vuông góc
5
3.
Các công thức tính thể tích khối đa diện
7
4.
PHẦN A: PHẦN NỀN TẢNG
5.
PHẦN I: VẼ CHIỀU CAO VÀ GÓC GIỮA ĐƯỜNG THẲNG VỚI MẶT PHẲNG.
8
6.
Dạng 1: Vẽ chiều cao cho trước
9
7.
Bài toán 1: Góc giữa đường thẳng với mặt phẳng
9
8.
Dạng 2: Mặt phẳng vuông góc với đáy
12
9.
Bài toán 1: Mặt phẳng chứa đỉnh là tam giác đều, cân
13
10.
Bài toán 2: Mặt phẳng chứa đỉnh là tam giác vuông
14
11.
PHẦN II: VẼ GÓC GIỮA HAI MẶT PHẲNG
24
12.
Dạng 3: Hai mặt phẳng vuông góc với đáy
17
13.
Dạng 4: Các cạnh bên bằng nhau và tạo với đáy một góc bằng nhau
18
14.
PHẦN III: VẼ KHOẢNG CÁCH
28
15.
Dạng 1: Khoảng cách từ 1 điểm đến một mặt phẳng
28
16.
Dạng 2: Khoảng cách hai đường chéo nhau
24
17.
Bài toán 1: Dạng kẻng song song để xác định khoảng cách
24
18.
Bài toán 2: Dạng xác định đường vuông góc chung
28
19.
PHẦN B: PHẦN TÍNH TOÁN
30
20.
KHOẢNG CÁCH TỪ MỘT ĐIỂM ĐẾN MỘT ĐƯỜNG THẲNG
30
21.
Dạng 1: Dạng đề cho cạnh bên
31
22.
Dạng 2: Dạng đề cho góc giữa đường thẳng với mặt phẳng
39
23.
Dạng 3: Dạng đề cho góc giữa hai mặt phẳng
50
24.
Dạng 4: Dạng đề cho tam giác vuông tại S.
59
25.
Dạng 5: Chứng minh một tính chất đề xác định
61
26.
Bài toán 1: Dạng đáy là hình thang
61
27.
Bài toán 2: Dạng đáy là hình vuông, hình chữ nhật
65
28.
KHOẢNG CÁCH GIỮA HAI ĐƯỜNG CHÉO NHAU
68
29.
Dạng 1: Khi không tìm được đường vuông góc chung
69
30.
Cho luôn khoảng cách giữa hai đường thẳng
69
31.
Kẻ song song để tìm khoảng cách
79
32.
Bài toán 1: Sử dụng phương pháp sole trong để tính khoảng cách
79
33.
Bài toán 2: Sử dụng tính chất hình vuông, hình chữ nhật
94
34.
Dạng 2: Tìm được đường vuông góc chung
103
35.
Lời giải chi tiết
109
Khóa học LUYỆN THI ĐẠI HỌC – Thầy Hiếu Live – 0988 593 390 – Facebook: Hiếu Live
Trung tâm Olympia – Uy Tín – Chất lượng – Tận Tâm Page 1
THỂ TÍCH KHỐI ĐA DIỆN
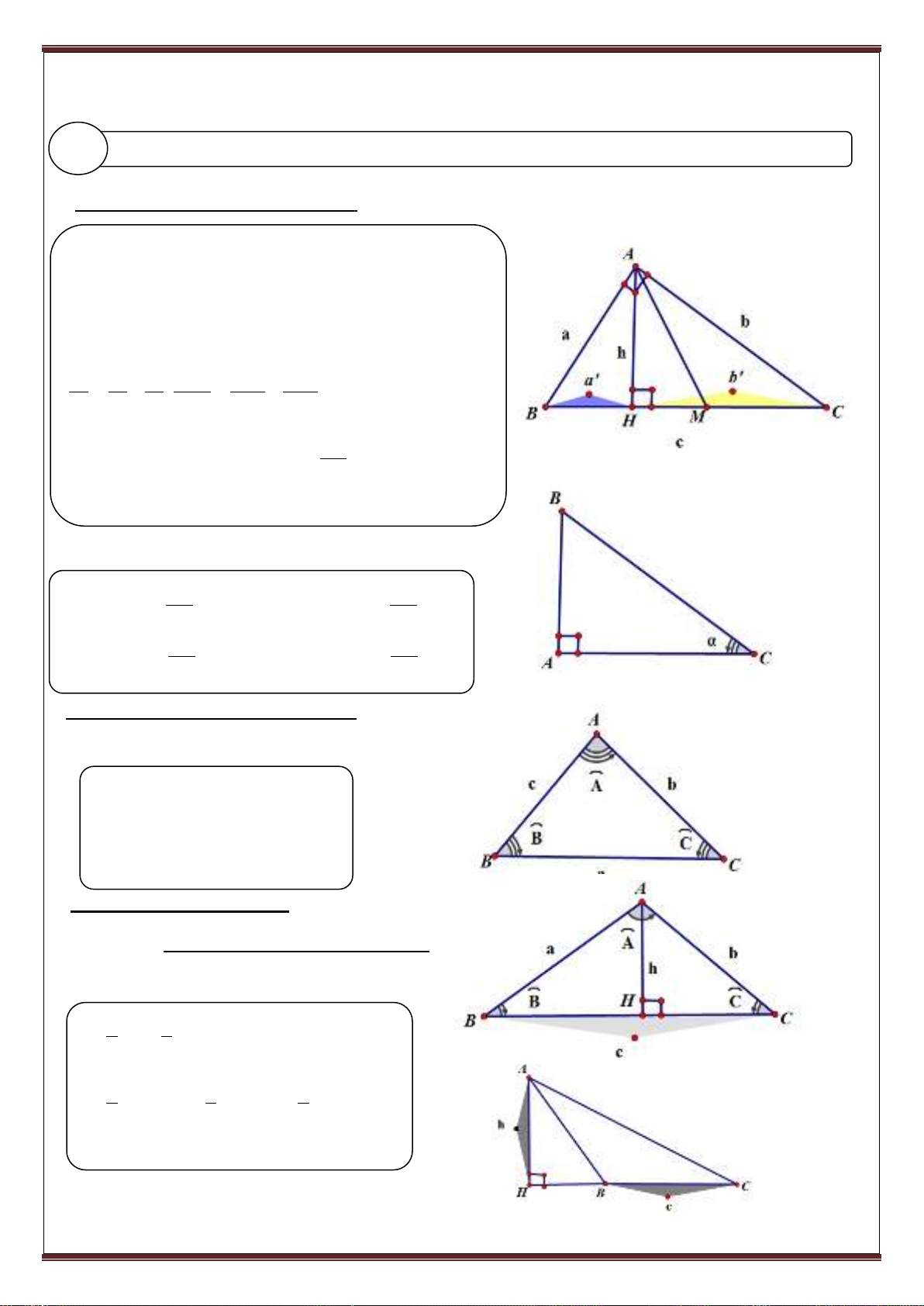
1. Hệ thức lượng trong tam giác vuông : Cho
ABC
vuông ở A có
AH BC
ta có :
Định lý Pitago :
2 2 2 2 2 2
c a b ; BC AB AC
22
a a '.c;b b'.c
;
22
BA BH.BC ; CA CH.CB
a.b c.h
; AB. AC = BC. AH
2 2 2 2 2 2
1 1 1 1 1 1
;
h a b AH AB AC
(Công thức khủng bố IS)
h a'.b'
; AH2 = BH.CH ;
BC
AM ;BC 2AM
2
(Đường trung tuyến bằng một nửa cạnh huyền)
AB
sin C BC
;
AC
cosC BC
AB
tan C AC
;
AC
cot C AB
2.Hệ thức lượng trong tam giác thường:
* Định lý hàm số Côsin:
2 2 2
2 2 2
2 2 2
a b c 2bc.cos A
b a c 2ac.cosB
c a b 2ab.cosC
3. Các công thức tính diện tích.
Công thức tính diện tích tam giác:
11
S h.c AH.BC
22
(Đáy x chiều cao)
1 1 1
S a.b.sin A a.csin B b.csinC
2 2 2
(Tích hai cạnh nhân sin góc xen giữa)
MỘT SỐ CÔNG THỨC GIẢI TAM GIÁC & CÔNG THỨC TÍNH DIỆN TÍCH
1
Khóa học LUYỆN THI ĐẠI HỌC – Thầy Hiếu Live – 0988 593 390 – Facebook: Hiếu Live
Trung tâm Olympia – Uy Tín – Chất lượng – Tận Tâm Page 2
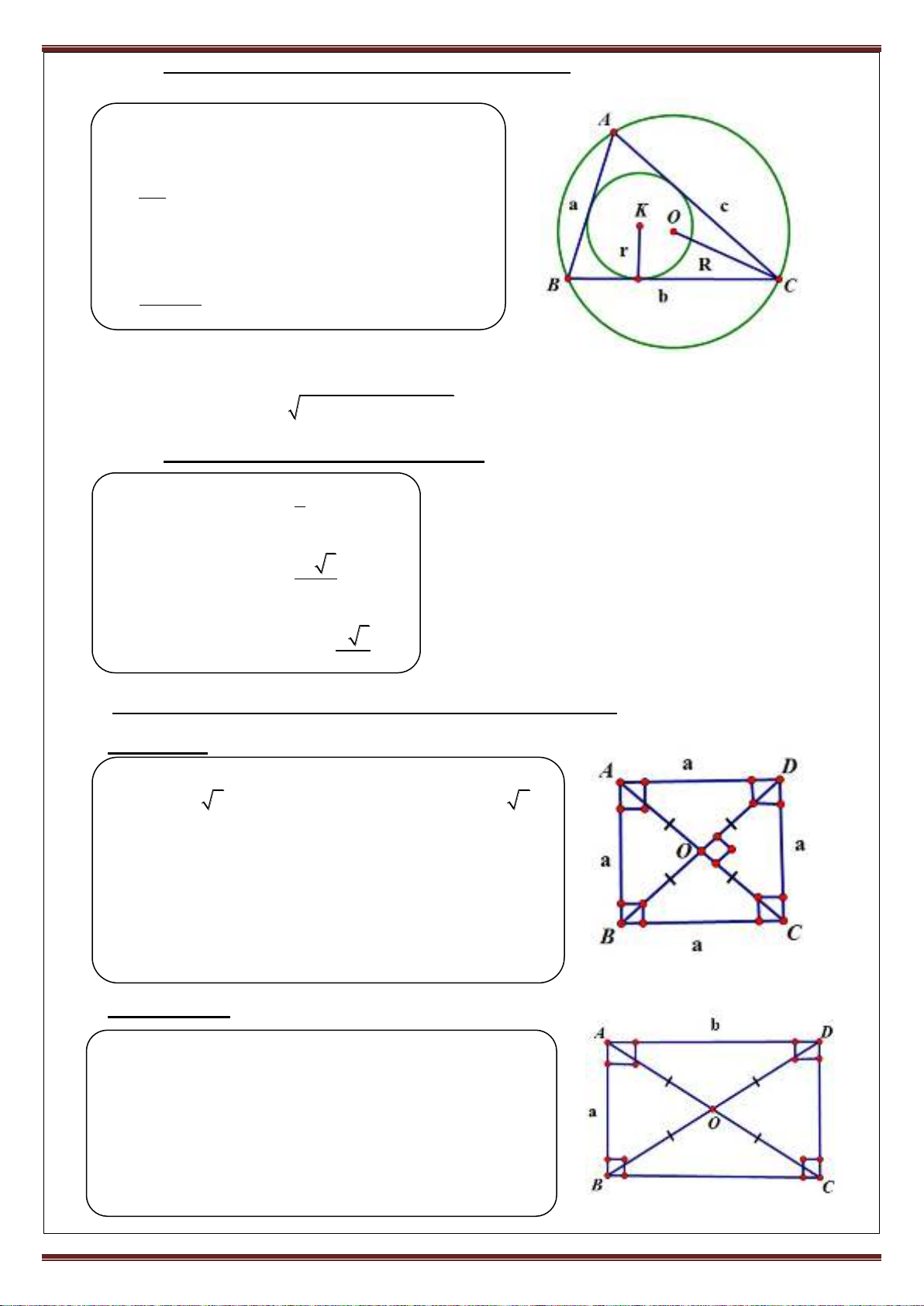
Công thức tính diện tích liên quan đến đường tròn:
Đường tròn ngoại tiếp tam giác tâm O bán kính R:
abc
S4R
(Tích 3 cạnh chia 4 lần bán kính)
Đường tròn nội tiếp tam giác tâm K bán kính r:
a b c
p2
(nửa chu vi)
S p.r
(nửa chu vi x bán kính)
Công thức Heron:
S p(p a)(p b)(p c)
Công thức tính nhanh tam giác đặc biệt:
ABC
vuông ở A :
1
S AB.AC
2
ABC
đều cạnh x:
2
x3
S4
Chiều cao tam giác đều:
x3
h2
b) Công thức tính diện tích tứ giác và tính chất! (Thường dùng)
Hình vuông:
22
S AB a
(Bình phương 1 cạnh)
AC AB 2
(Đường chéo bằng cạnh bên nhân
2
)
AC BD
(Hai đường chéo vuông góc)
OA = OB = OC = OD (O là tâm đường tròn ngoại tiếp)
0
BAC CAD ADB BDC ... 45
(Đường chéo chia đôi góc vuông)
AD / /BC;AB/ /DC
(các cặp cạnh đối song song)
Hình chữ nhật:
S a.b AB.AD
(Chiều dài x chiều rộng)
OA = OB = OC = OD (O là tâm đường tròn ngoại tiếp)
AD / /BC AB / /DC
;
AD BC AB BC
(các cặp cạnh đối song song và bằng nhau)
Khóa học LUYỆN THI ĐẠI HỌC – Thầy Hiếu Live – 0988 593 390 – Facebook: Hiếu Live
Trung tâm Olympia – Uy Tín – Chất lượng – Tận Tâm Page 3
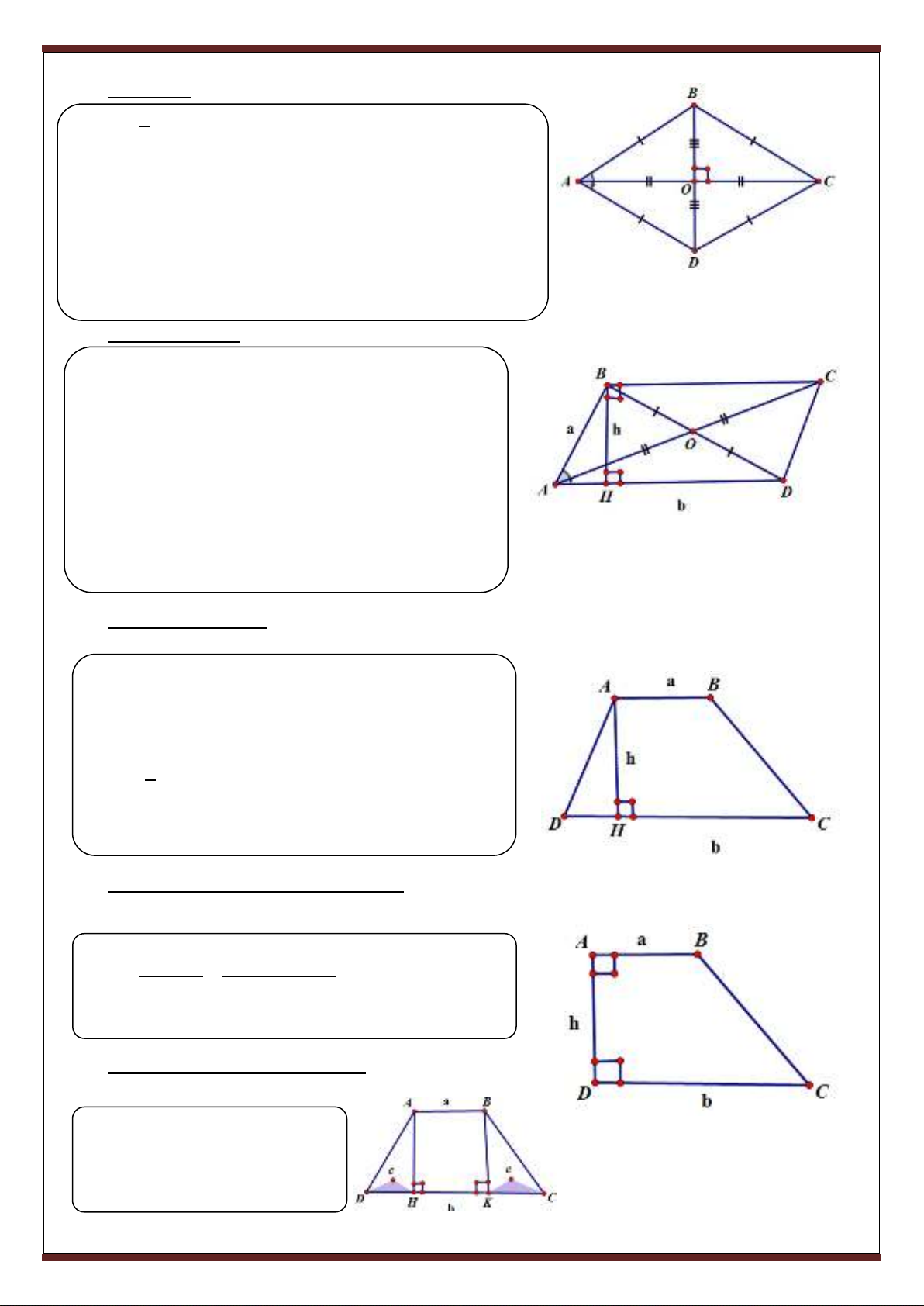
Hình thoi:
2
1
S AC.BD AB sin BAD
2
(Tích 2 đường chéo chia 2)
(Hoặc bình phương cạnh nhân sin góc xen giữa)
AC BD
(Hai đường chéo vuông góc)
OA OC
OB OD
AC#BD
(O là trung điểm của 2 đường chéo)
AD / /BC;AB/ /DC
(các cặp cạnh đối song song)
Hình bình hành:
S b.h AD.BH a.bsin BAD
(Chiều cao x đáy)
(Hoặc tích hai cạnh bên nhân sin góc xen giữa)
OA OC
OB OD
AC#BD
(O là trung điểm của 2 đường chéo)
AD / /BC AB / /DC
;
AD BC AB BC
(các cặp cạnh đối song song và bằng nhau)
Hình thang thường:
(a b).h (AB CD).AH
S22
(
1
S2
(đáy lớn + đáy nhỏ) x chiều cao)
AB/ /CD
Hình thang thường có hai góc vuông:
(a b).h (AB CD).AD
S22
AD là chiều cao của hình thang
Hình thang cân: (Tính chất nhỏ)
DH KC c
b 2c a
DC 2DH AB


























