CHƯƠNG 9
THANH CHỊU LỰC PHỨC TẠP
KHÁI NIỆM CHUNG
I. UỐN XIÊN
1. Khái niệm
2. Ứng suất pháp
3. Ðường trung hòa và biểu đồ ứng suất
4. Kiểm tra bền
5. Ðộ võng của dầm khi uốn xiên
II. THANH CHỊU UỐN VÀ KÉO (NÉN) ÐỒNG THỜI
1. Khái niệm
2. Ứng suất
3. Ðiều kiện bền
III. THANH CHỊU UỐN VÀ XOẮN ÐỒNG THỜI
1. Uốn và xoắn đối với thanh tròn
2. Uốn và xoắn đồng thời thanh mặt cắt ngang chữ nhật
IV. THANH CHỊU LỰC TỔNG QUÁT
1. Thanh có mặt cắt ngang tròn chịu lực tổng quát
2. Thanh có mặt cắt ngang chữ nhật chịu lực tổng quát
V. LÕI CỦA MẶT CẮT
KHÁI NIỆM CHUNG TOP
Các dạng chịu lực của thanh mà chúng ta nghiên cứu trước đây như kéo, nén đúng tâm,
xoắn thuần tuý, uốn thuần túy phẳng và uốn ngang phẳng đều thuộc về những trường hợp
chịu lực đơn giản của thanh.
Trong chương này ta nghiên cứu các trường hợp chịu lực phức tạp của thanh nghĩa là
những hình thức chịu lực kết hợp giữa các trường hợp chịu lực đơn giản. Các bài toán thường
gặp là uốn xiên, uốn và kéo đồng thời và trường hợp chịu lực tổng quát.
Ðể giải quyết những bài toán đó, chúng ta sử dụng nguyên lý độc lập tác dụng. Nguyên lý
đó được phát biểu như sau:
Ưïng suất và biến dạng do nhiều yếu tố gây ra đồng thời trên một thanh bằng tổng ứng suất
và biến dạng do từng yếu tố riêng biệt gây ra trên thanh đó .
Muốn sử dụng được nguyên lý này, bài toán phải thỏa mãn các điều kiện sau đây :
Vật liệu làm việc trong giới hạn đàn hồi, quan hệ giữa ứng suất và biến dạng là bậc nhất
Biến dạng của thanh là bé, sự chuyển dịch điểm đặt của lực tác dụng lên thanh là không
đáng kể
Khi xét bài toán chịu lực phức tạp, vì ảnh hưởng của lực cắt đến độ bền của thanh không đáng
kể so với các thành phần nội lực khác, nên trong mọi trường hợp chúng ta đều không xét đến
lực cắt.
I. UỐN XIÊN
1. Khái niệm TOP
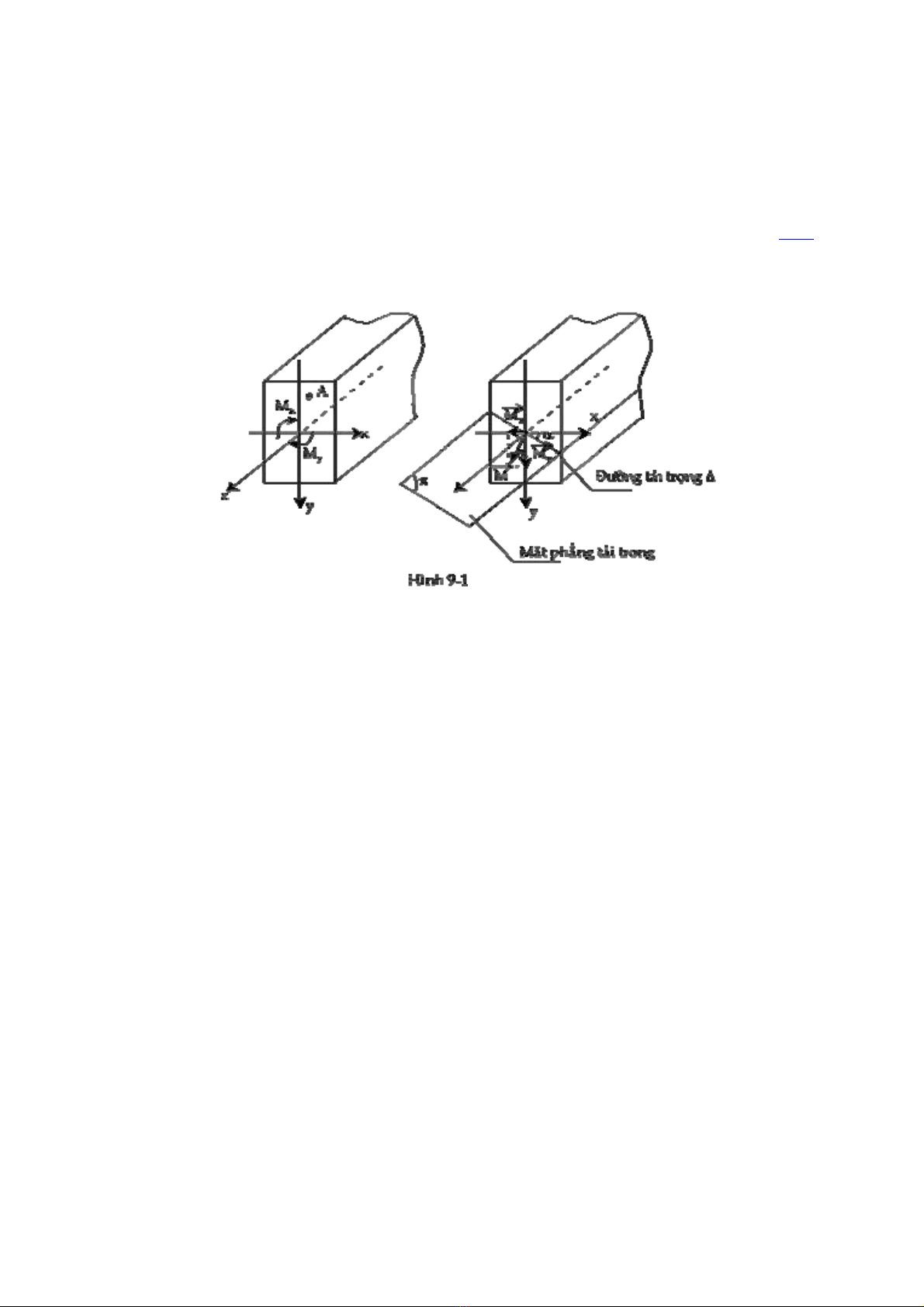
Thanh uốn xiên là thanh mà trên mọi mặt cắt ngang chỉ có 2 thành phần nội lực là các
momen uốn Mx, My nằm trong các mặt phẳng quán tính chính trung tâm của mặt cắt.
Biểu diễn các momen uốn Mx, My bằng các vectơĠ,Ġ.Hợp hai vectơ này lại ta được
vectơ tổng hợpĠ. Khi hợp hai momen uốn Mx, My lại ta được momen uốn tổng hợp M nằm
trong mặt phẳng ( chứa trục z của thanh. Ta thấy mặt phẳng (không trùng với một mặt phẳng
quán tính chính trung tâm nào của mặt cắt ngang.
Mặt phẳng ( được gọi là mặt phẳng tải trọng
Giao tuyến của mặt phẳng tải trọng và mặt cắt ngang là đường tải trọng . Ðường tải trọng
là đường thẳng đi qua gốc tọa độ và vuông góc với phương của vectơ tổng momen M. Từ đó
ta có một định nghĩa khác về uốn xiên như sau :
Thanh chịu uốn xiên là thanh chịu lực sao cho trên mọi mặt cắt ngang của thanh chỉ có một
thành phần nội lực là momen uốn M nằm trong mặt phẳng chứa trục z của thanh nhưng không
trùng với mặt phẳng quán tính chính trung tâm nào của mặt phẳng ngang.
Gọi ( là góc có hướng giữa trục x và đường tải trọng, ( sẽ dương khi chiều quay từ trục x
đến đừơng tải trọng là thuận chiều kim đồng hồ , ngược lại ( âm .
Cũng như trước đây dấu của các momen uốn Mx , My được quy ước như trong trường hợp
thanh chịu uốn phẳng nghĩa là Mx , My được coi là dương khi nó làm căng các thớ ở về phía
dương của trục x và trục y.
Ta thấy sự tương quan giữa Mx , My và M như sau:
Mx = Msinα
My = Mcosα
Như vậy hệ số góc của đường tải trọng là
:Ġ (IX-1)
2. Ứng suất pháp TOP
Aïp dụng nguyên lý độc lập tác dụng, ta có thể xem ứng suất tại một điểm A nào đó trên
mặt cắt ngang là tổng ứng suất do momen uốn Mx và My gây nên một cách riêng lẽ. Như vậy
ta đã đưa bài toán trên về 2 bài toán uốn thuần tuý đơn. Gọi x và y là tọa độ của một điểm A
nào đó, trị số ứng suất tại A là:
(IX-2a)
Khi sử dụng công thức đó ta phải chú ý đến dấu của Mx , My và x, y nên để thuận tiện ta
dùng công thức kỹ thuật sau đây:
(IX-2b)
Trong đó các giá trị đều lấy giá trị tuyệt đối, còn dấu (+) hay (-) trước mỗi số hạng thì tùy
theo các momen uốn Mx , My gây ra ứng suất kéo hay nén ở điểm đang xét.
Giả sử xét ứng suất tại A trên hình 9-1 . Ðối với Mx , ứng suất tại A là nén, vậy trước số
hạng chứa Mx lấy dấu âm; đối với My ứng suất tại A là kéo, vậy trước số hạng chứa My, lấy
dấu dương.
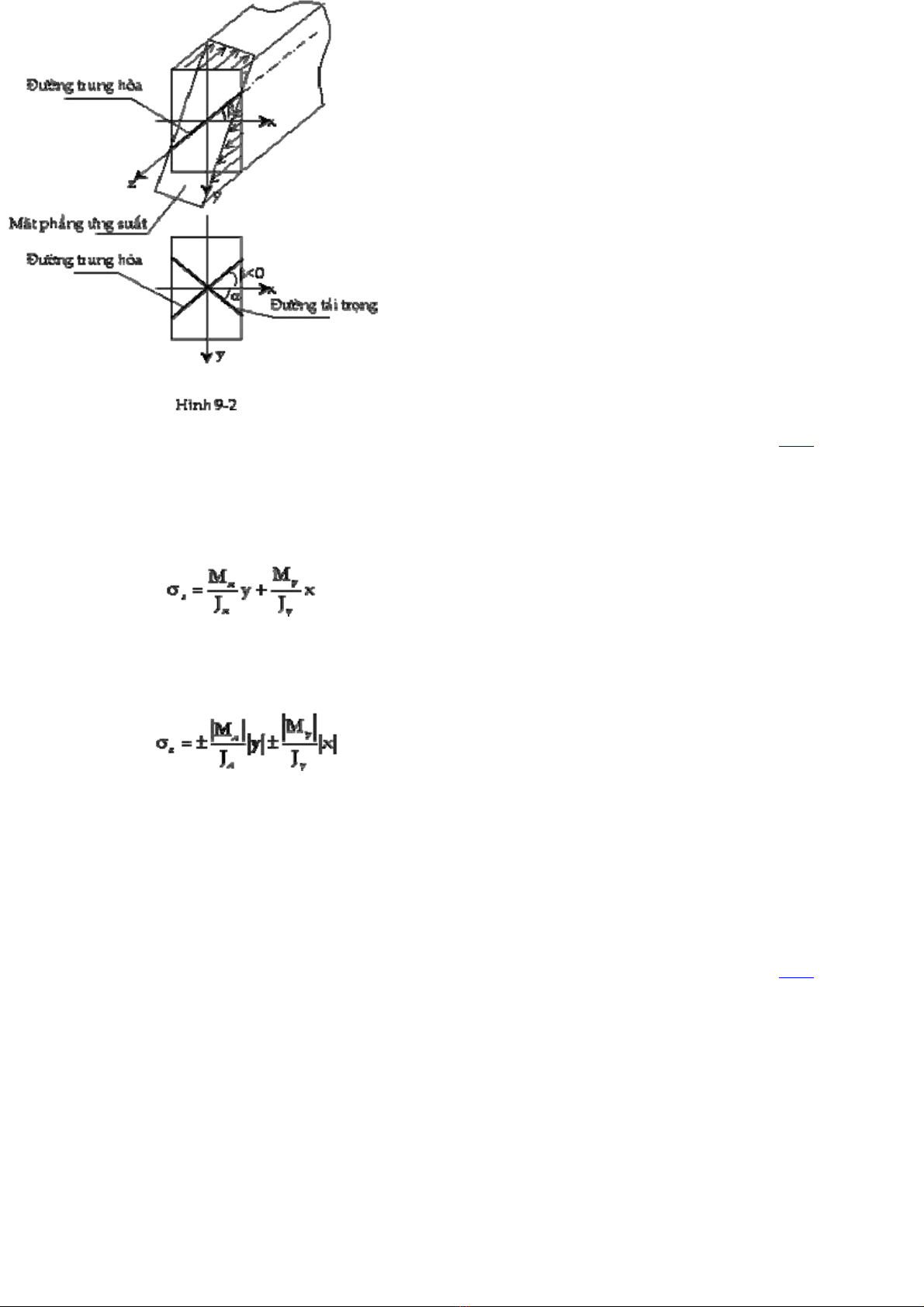
3. Ðường trung hòa và biểu đồ ứng suất
a./ Ðường trung hòa TOP
Ta thấy phương trình biểu diễn ứng suất tại một điểm mọi trên mặt cắt ngang là một hàm 2
biến theo x và y, đây là phương trình biểu diễn một mặt phẳng. Ta gọi mặt phẳng này là mặt
phẳng ứng suất.
Giao tuyến của mặt ứng suất với mặt
cắt ngang là quỹ tích những điểm cùng có giá trị ứng suất pháp bằng không. Giao tuyến đó
chính là đường trung hòa, phương trình của nó là:
(IX-3)
Hay y = tgβ.x
Trong đó tg( là hệ số góc của đường trung hòa
(IX-4)
Ta thấyĠ
Nhận xét :
Góc ( và ( luôn luôn trái dấu nhau. Thực vậy vì Jx và Jy là những số dương, do đó dấu của
tg( luôn ngược dấu với tg(. Như vậy đường tải trọng và đường trung hòa không bao giờ cùng
nằm trong một góc phần tư của hệ trục tọa độ.
Thông thường đường trung hòa và đường tải trọng không vuông góc với nhau
Thật vậy vì Ġ trong đó JxĠJy
Nếu Jx = Jy thì Ġ khi đó đường trung hòa vuông góc với đường tải trọng và bất kỳ trục nào
đi qua trọng tâm mặt cắt cũng là trục quán tính chính trung tâm. Như vậy mặt phẳng tải trọng
cũng là mặt phẳng quán tính chính trung tâm. Sự uốn của thanh không còn là uốn xiên nữa mà
là uốn thuần túy đơn. Ðó là trường hợp mặt cắt ngang của thanh là hình tròn hoặc đa giác đều.
Với những thanh đó thì không bao giờ chịu uốn xiên.
b./ Biểu đồ ứng suất TOP
Biều đồ ứng suất trên mặt cắt ngang được vẽ như sau:
Kéo dài đường trung hòa ra khỏi mặt cắt, vẽ đường vuông góc
với đường trung hòa làm đường chuẩn. Ưïng suất tại các điểm trên đường thẳng song song
với đường trung hòa được biểu diễn bằng một đoạn thẳng có gốc trên đường chuẩn và có
phương nằm trên đường thẳng song song đó.
Từ biểu đồ mặt ứng suất ta nhận thấy những điểm cùng nằm trên một đường thẳng song
song với đường trung hòa thì cùng có ứng suất như nhau. Trị số các ứng suất tỉ lệ với khoảng
cách đến đường trung hòa.
Từ biểu đồ ứng suất trên mặt cắt ngang ta tìm được các điểm nguy hiểm trong miền chịu
kéo và nén. Những điểm này là những điểm nằm xa đường trung hòa nhất.
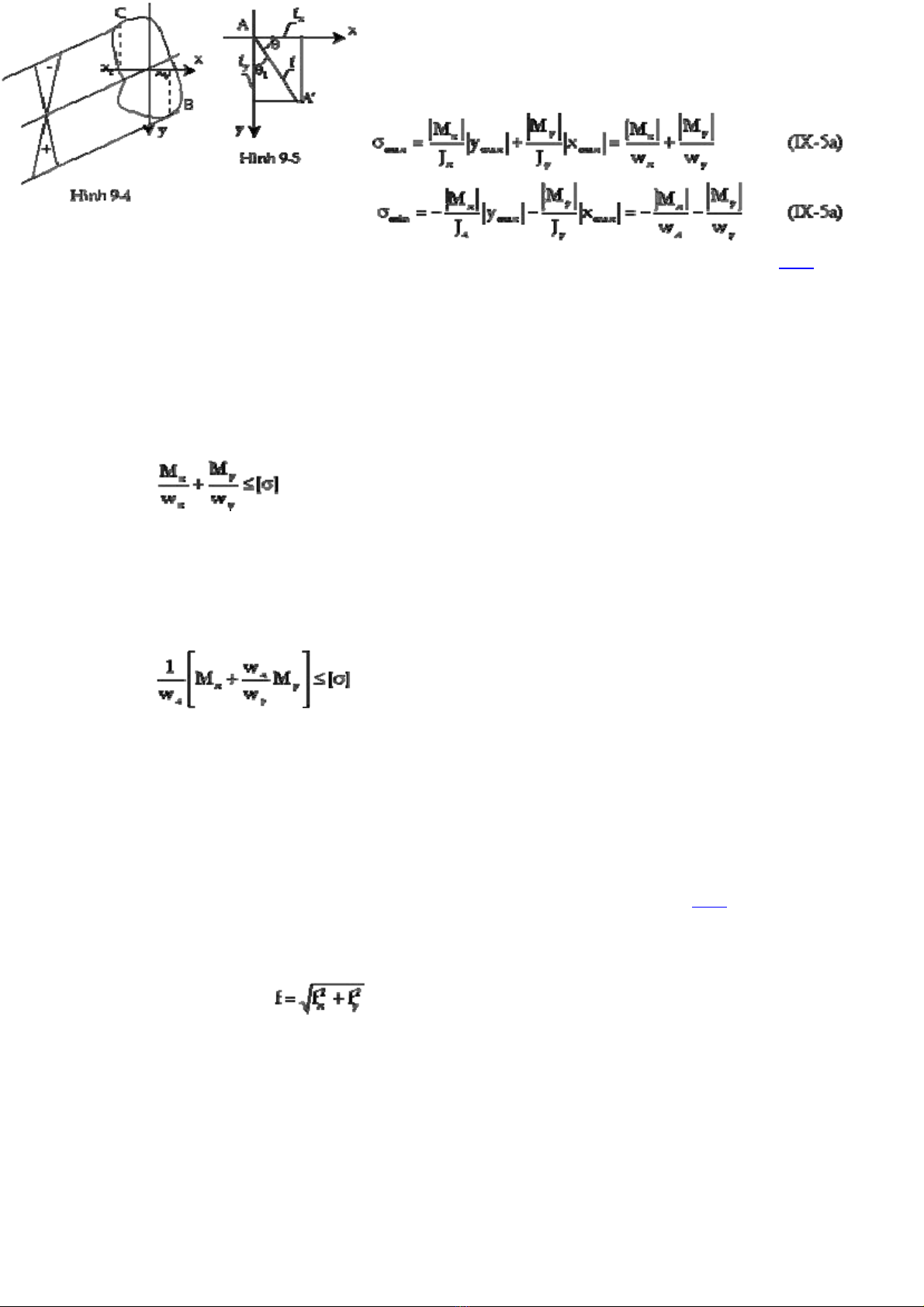
Ðối với mặt cắt ngang hình chữ nhật, chữ I, điểm nguy hiểm luôn luôn là các góc (điểm
B và C hình 9-3)
Các trị số ứng suất cực đại và cực tiểu là:
4. Kiểm tra bền TOP
Ðiều kiện bền của dầm chịu uốn xiên là:
σmax ≤ [σk]
σmin ≤ [σn]
Ðối với vật liệu dẻo, mặt cắt ngang thường là hình chữ nhật, chữ I hoặc tương tự, vì [(k] =
[(n] nên điều kiện bền có thể viết lại là:
Từ phương trình trên ta thấy đối với bài toán chọn mặt cắt ngang ta gặp hai ẩn số là wx và
wy. Ta chọn trước một ẩn số, từ đó xác định ẩn số thứ hai, xong kiểm tra lại từ điều kiện bền,
làm như vậy cho đến khi xác định được kích thước hợp lý nhất.
Thường để giải quyết bài toán được nhanh chóng ta viết điều kiện bền lại như sau:
(IX-6)
Rồi chọn trước tỷ sốĠ, việc chọn tỷ số này đơn giản hơn việc chọn wx hay wy.
- Ðối với mặt cắt ngang chữ nhật ĠĽ
- Ðối với mặt cắt ngang chữ U Ġ= 5 ( 7
- Ðối với mặt cắt ngang chữ I Ġ= 8 ( 10
Ðối với mặt cắt ngang dạng bất kỳ, điểm nguy hiểm vẫn là điểm xa trục trung hòa nhất
(B và C)
5. Ðộ võng của dầm khi uốn xiên TOP
Gọi fx và fy là độ võng do Mx và My gây ra tại mặt cắt nào đó. Ðộ võng toàn phần f sẽ
bằng tổng hình học của fx và fy
Với cách đó ta có thể xác định được độ võng tại các mặt cắt khác nhau và như vậy ta có thể
xác định được đường đàn hồi của dầm.
Nếu đường đàn hồi nằm ngang trong mặt phẳng thì ta có uốn xiên phẳng, nếu là một đường
cong ghềnh thì gọi là uốn xiên không gian
Phương của chuyển vị: