CHƯƠNG 11
THANH CONG PHẲNG
I. KHÁI NIỆM
II. ỨNG SUẤT PHÁP TRONG THANH CONG PHẲNG CHỊU UỐN THUẦN TÚY
1. Giả thuyết mặt cắt ngang phẳng
2. Giả thuyết về các thớ dọc
III. TÍNH THANH CONG CHỊU LỰC PHỨC TẠP
IV. XÁC ÐỊNH VỊ TRÍ ÐƯỜNG TRUNG HÒA ÐỐI VỚI MỘT SỐ MẶT CẮT
NGANG ÐƠN GIẢN
1. Mặt cắt ngang hình thang
2. Mặt cắt ngang hình tam giác
3. Mặt cắt ngang hình chữ nhật
4. Mặt cắt ngang hình tròn
5. Phương pháp gần đúng để tính rth
6. Xác định rth theo bảng
I. KHÁI NIỆM TOP
Khi trục thanh có dạng thẳng ta có thanh thẳng
Khi trục thanh có dạng cong ta có thanh cong. Ví dụ: vòng xích, móc cầu trục...
Aính hưởng của độ cong đến độ bền của thanh được đặc trưng bởi tỉ sốĠ trong đó:
h: chiều cao của mặt cắt ngang
(: bán kính cong của trục tại mặt cắt ngang có chiều cao h đang xét.
Khi thanh có độ cong bé, nghĩa làĠ thì ứng suất trên mặt cắt ngang của thanh cong gần
giống thanh thẳng
Ví dụ: khi Ġ thì (max chênh lệch 4,6% còn (min lệch khoảng 7% , khũ thì (max chênh
lệch 1,5% còn (min lệch khoảng 3% so với thanh thẳng
Khi thanh có độ cong lớn, nghĩa là Ġthì ứng suất trên mặt cắt ngang của thanh cong và
thanh thẳng khác nhau nhiều.
Vì vậy đối với thanh
cong có độ cong bé ta coi
như thanh thẳng ở đây ta chỉ
tính toán đối với thanh cong
có độ cong lớn. Giới hạn
nghiên cứu như sau:
a. Thanh cong phẳng
có các trục đối xứng nằm
trong mặt phẳng chứa trục Z
của thanh, ta gọi đó là mặt phẳng đối xứng của
thanh.
b. Tải trọng tác dụng lên thanh đều nằm
trong mặt phẳng đối xứng của thanh.
Nếu trên mặt cắt ngang của thanh có momen uốn Mx ta gọi thanh chọn uốn thuần túy
phẳng.
Nếu trên mặt cắt ngang có đầy đủ ba thành phần nội lực Mx, Qy , Nz ta gọi thanh chịu
lực phức tạp.
II. ỨNG SUẤT PHÁP TRONG THANH CONG PHẲNG CHỊU UỐN THUẦN
TÚY TOP
Cũng như trong thanh thẳng, thanh cong chịu uốn thuần túy có những thớ trung hòa,
những thớ trung hòa tạo thành lớp trung hòa. Giao tuyến của lớp trung hòa với mặt cắt ngang
gọi là đường trung hòa. Vì lý do đối xứng nên đường trung hòa vuông góc với mặt đối xứng
của thanh. Khác với thanh thẳng, đường trung hòa trong thanh cong không đi qua trọng tâm
của mặt cắt ngang.
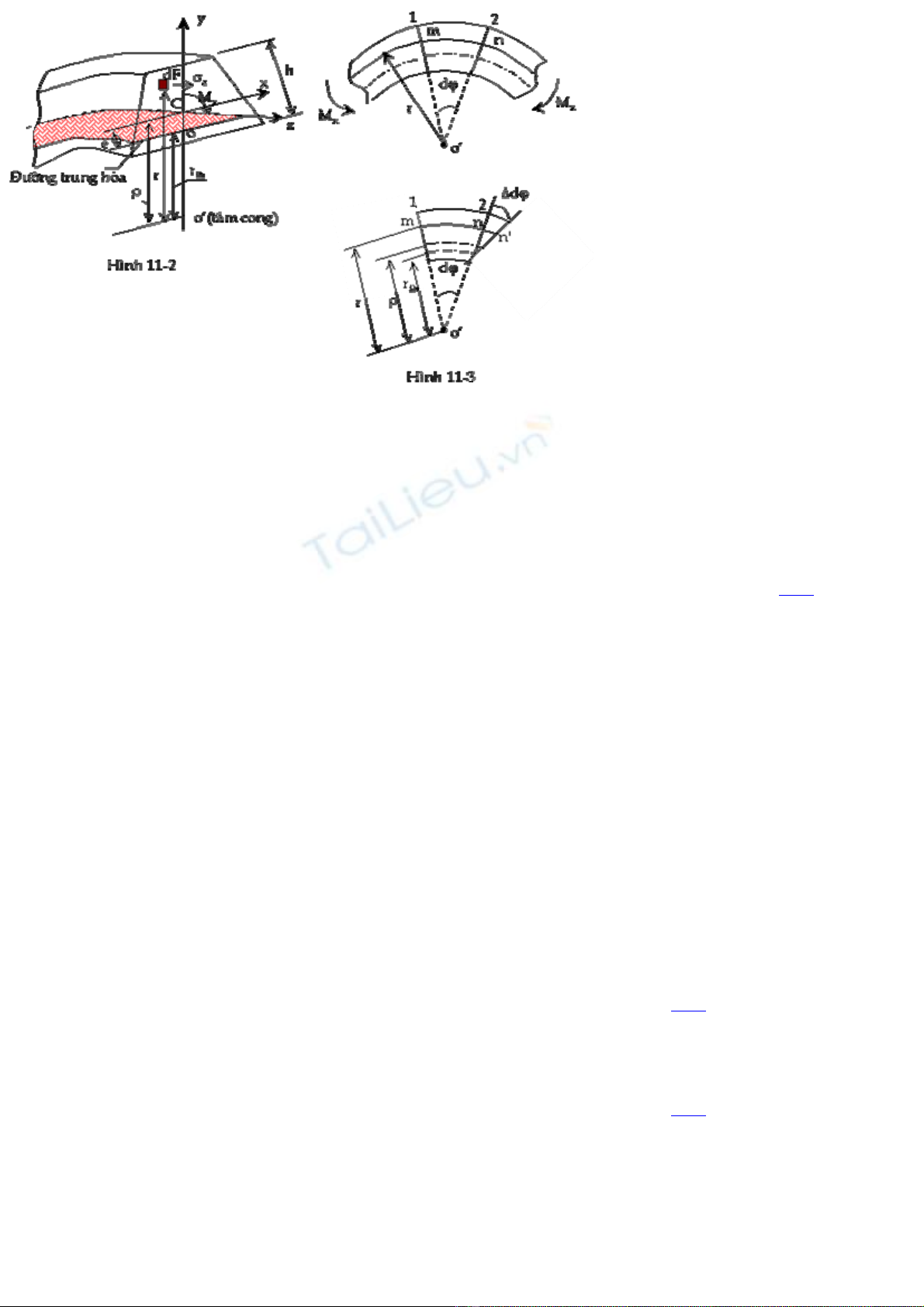
Gọi C là trọng tâm của mặt cắt ngang đang xét. Hệ trục tọa độ Cxyz được chọn như
hình vẽ 11-2, trong đó chiều dương của trục Y hướng từ tâm cong O ra ngoài.
Như vậy momen uốn Mx được coi là dương khi làm cho thanh bị cong thêm (cong về
phía chiều dương của trục y)
a)
Ðể tính ứng suất và biến dạng của thanh cong ta dựa vào hai giả thuyết sau:
1. Giả thuyết mặt cắt ngang phẳng TOP
Trước và sau khi bị biến dạng mặt cắt ngang của thanh vẫn phẳng và vuông góc với trục
của thanh.
2. Giả thuyết về các thớ dọc TOP
b)
Trong quá trình biến dạng, các thớ dọc (thớ song song với trục cong của thanh) không
ép lên nhau và cũng không tách xa nhau.
Xét một đoạn thanh cong giới hạn bởi hai mặt cắt 1-1 và 2-2 hợp với nhau một góc d(. Sau
khi biến dạng, mặt cắt ngang 2-2 xoay đi một góc (d( so với mặt cắt ngang 1-1 quanh đường
trung hòa (hình 11-3a, b).
Chiều dài thớ mn trước biến dạng
ds = mn = r.dϕ
Ðộ dãn dài của thớ mn sau biến dạng là
Dds = (r - rth).Δdϕ
Ðộ biến dạng tỉ đối:Ġ
Theo giả thuyết mặt cắt ngang phẳng ta có (zx = (zy = 0
Theo giả thuyết các thớ dọc ta có (x = (y = 0
Vậy trạng thái của điểm đang xét là trạng thái ứng suất đơn. Theo định luật Húc:
Xác định (z : ta có ĉ (XI- 1b)
Ta có:
Thế (z vào: Ġ
Vì Ġ= const đối với mọi điểm trên mặt cắt nên
VìĠ( 0 (Ġ
Ta cóĠ
VậyĠ (XI-2)
Ðó là công thức để xác định bán kính cong rth của thớ trung hòa
Nếu lấy tổng momen của các ứng lực (z.dF đối với tâm cong O, ta được:
Thay (z từ công thức (XI-1b) vào (XI-3) ta được:
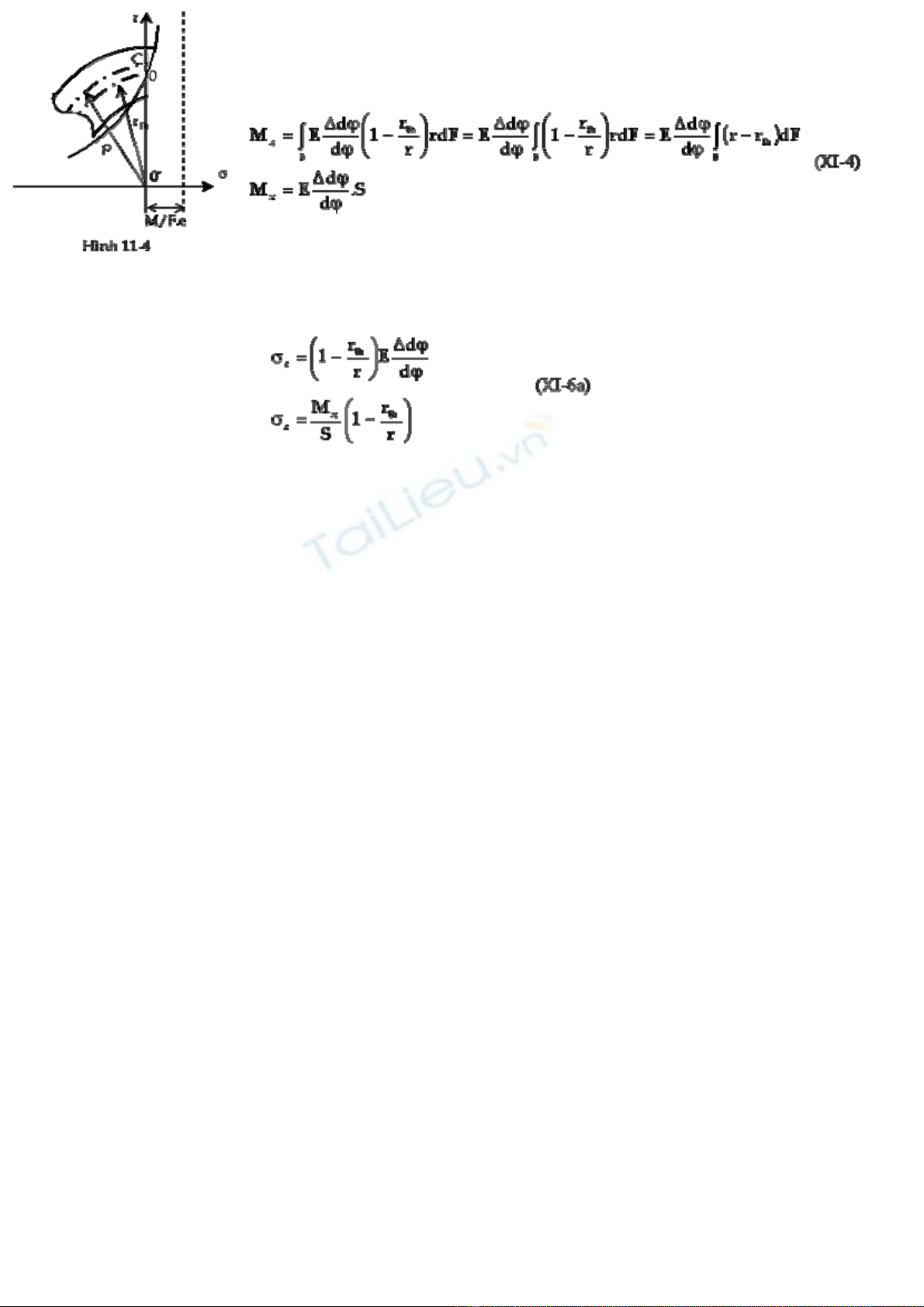
Trong đó:Ġ= moment tĩnh của mặt cắt ngang đối với đường trung
hòa
Thay tỷ số trên vào các biểu thức (XI-1b) ta có
Vậy Ġ (XI-5)
Nếu gọi e khoảng cách từ trọng tâm mặt cắt ngang đến trục trung hòa
Ta có S = F.e ; F: diện tích mặt cắt; S : momen tĩnh của mặt cắt ngang đối với trục trung
hòa
Vậy Ġ (XI-6b)
Trong đó: Mx: momen uốn trên mặt cắt ngang
ang đến trục trung hòa
cong
hypecbol, những điểm có cùng khoảng cách đến tâm cong thì ứng suất pháp bằng nhau.
g với pháp tuyến của mặt cắt (trục (z), và đườngĠ song song
với trục đối xứng của mặt cắt.
ở phía trong ngắn hơn nên có biến dạng
dài tương đốïi lớn hơn, do đó có ứng suất lớn hơn.
h cong
thường có kích thước ngang lớn về phía tâm cong (để đưa trọng tâm gần xuống đáy).
F: diện tích mặt cắt ngang
e: khoảng cách từ trọng tâm mặt cắt ng
rth: bán kính cong của thớ trung hòa
r: bán kính cong của điểm đang xét ; với (y = r - rth)
Từ công thức của (z ta thấy biểu đồ của (z dọc theo bán kính r là một đường
Ðường cong hypecbol đó có hai đường tiệm cận vuông góc với nhau. Ðó là đường đi
qua tâm cong đồng thời song son
Từ biểu đồ hình 11-4 ta nhận thấy những điểm ở phía ngoài đường trung hòa r > rth có
ứng suất pháp tăng chậm theo chiều cao của mặt cắt, còn các điểm ở phía tâm cong r < rth
có ứng suất tăng nhanh. Sở dĩ như thế vì theo giả thuyết mặt cắt phẳng, các thớ có cùng một
khoảng cách và ở hai phía đối với thớ trung hòa thì có biến dạng dài tuyệt đối như nhau,
nhưng chiều dài ban đầu của chúng khác nhau, thớ
Những điểm ở ngoài cùng r = rmax và ở trong cùng r = rmin có ứng suất pháp lớn nhất
về kéo và nén. Ðối với mặt cắt có bề rộng không đổi thì giá trị tuyệt đối ứng suất của điểm ở
phía trong lớn hơn. Ðể làm giảm trị số ứng suất ở mép trong, mặt cắt ngang của than
III. TÍNH THANH CONG CH
Trong thanh cong chịu lực phức tạp, nội lực gồm 3 thành phần là momen uốn Mx , lực
cắt Qy và lực dọc Nz . Aïp dụng nguyên , ta tính ứng suất do từng nội lực
gây ra.
Ứng suất pháp do Mx gây raĠ
Ứng suất pháp trong tạp
ỊU LỰC PHỨC TẠP
lý độc lập tác dụng
Ứng suất do Nz gây raĠ
thanh cong chịu lực phức
(XI-7)
Lấy lực cắt Qy chỉ gây ứ
pháp. Ưïng suất tiếp đó có thể t
ng suất tiếp mà không ảnh hưởng đến sự phân bố của ứng suất
ính gần đúng theo công thức Durápski của thanh thẳng
(XI-8)
Chú ý hệ trục xy là hệ trục quán tính chính trung tâm của mặt cắt ngang.
ÐỊNH VỊ TRÍ ÐƯỜNG TRUNG HÒA ÐỐI VỚI MỘT SỐ MẶT CẮT
NGANG ÐƠN GIẢN
cắt ngang hình thang
Ta cóĠ
IV. XÁC
1. Mặt
Theo công thức