1
BÀI TẬP NHÓM
HỌC PHẦN: ĐÁNH GIÁ TRONG DẠY HỌC TOÁN
ĐỀ TÀI: PHÂN LOẠI CÁC MỤC TIÊU GIÁO DỤC TOÁN
THEO CÁC MỨC ĐỘ NHẬN THỨC CỦA BLOOM VỀ
CHỦ ĐỀ QUAN HỆ SONG SONG.
Nhóm thực hiện: Nhóm 2, Toán 4A
Thành viên: 1. Hoàng Thị Lê.
2.Trương Thị Diệu Loan.
3.Nguyễn Thị Mai Trang.
4. Trần Thị Thoa.
2
Trong bài tiểu luận này nhóm xin trình bày sự phân loại các mục tiêu giáo dục toán
theo các mức độ của nhận thức của Bloom về đề tài: Quan hệ song song.
Sơ đồ thang nhận thức của Bloom như sau:
I. N
-Nâ .
1. N
1.1.
-Phát biểu đư c các định ngh a vị tr tương đ i của hai đư ng th ng trong h ng
gian đồng ph ng, ch o nhau, song song , đư ngth ng song song v i m t ph ng, m t
ph ng song song v i m t ph ng, ph p chi u song song, hình biểu diễn của một hình
trong h ng gian hình l ng trụ, hình hộp, hình chóp cụt).
-Bi t đư c các hiệu :
-Trong định ngh a ph p chi u song song h c sinh ph i bi t đư c : P là m t ph ng
chi u, là phương chi u , là hình chi u song song của điểm qua ph p chi u nói
trên.
-Nh các định l , t nh ch t, hệ qu của chương này
1.2. N
- ác định giao tuy n của hai m t ph ng c t nhau chứa hai đư ng th ng song song
Những
kh n ng
bậc cao
Vận dụng
Th ng hiểu
Nhận bi t
3
- ác định giao tuy n của hai m t ph ng c t nhau c ng song song v i một đư ng
th ng cho trư c.
- ác định tâm của hình hộp.
- ác định hình biểu diễn của đư ng th ng, đoạn th ng, tia, đư ng tr n, hai đư ng
th ng song song qua ph p chi u song song.
2. T
2.1. :
-Chuyển đ i các hái niệm hình h c cho dư i dạng l i sang dạng hình v trong h ng
gian.
- i t dư i dạng hiệu của định l , t nh ch t, hệ qu cho b ng l i và ngư c lại.
2.2.
-Hiểu đư c các bư c chứng minh của các định l , t nh ch t, hệ qu .
-Có h n ng tóm t t một bài toán hình h c h ng gian b ng hiệu.
-Th y đư c t nh đ i xứng qua tâm của hình hộp.
-Nêu đư c phương pháp chứng minh đư ng th ng đồng quy.
-Nêu đư c các phương pháp chứng minh đư ng th ng song song v i m t ph ng.
- Nêu đư c các phương pháp chứng minh hai m t ph ng song song v i nhau.
2.3. N
- ác định thi t diện của một hình c t b i một m t ph ng cho trư c.
-L y đư c v dụ trực quan: hình l ng trụ, hình hộp, hình chóp cụt có trong thực t .
-Qua ph p chi u song song bi n trung điểm của một đoạn th ng thành trung điểm
đoạn th ng.
3.
- p dụng các t nh ch t và đinh l có trong chương quan hệ song song để chứng minh
các bài toán liên quan đ n quan hệ song song: giữa đư ng th ng v i đư ng th ng,
đư ng th ng v i m t ph ng, m t ph ng v i m t ph ng.
-Ngoài việc s dụng các i n thức đ bi t liên quan đ n quan hệ song song trong
h ng gian h c sinh cần t h p các t nh ch t trong hình h c ph ng để gi i toán và
dựng thi t diện.
4
4. N
-Kh ng ph i bài toán nào h c sinh cũng dễ dàng vận dụng các quy t c hay phương
pháp chung để gi i quy t, có những trư ng h p h c sinh ph i tr i qua một quá trình
phân t ch, t ng h p, đánh giá m i có thể đưa bài toán về trư ng h p quen thuộc để
gi i.
-Sau khi h c xong chương quan hệ song song h c sinh ph i bi t phân t ch gi thi t bài
toán thanh những phần ch nh và thi t lập m i quan hệ song song giữa đư ng th ng v i
đư ng th ng, đư ng th ng v i m t ph ng, m t ph ng v i m t ph ng.
-Từ gi thi t sau quá trình phân t ch h c sinh định hư ng đư c mình s vận dụng định
l quy t c, phương pháp nào để gi i bài toán có tình hu ng từ đó đưa về tình hu ng
quen thuộc.
II. N
1. N
1.1.
V d 1: Mệnh đề nào sau đây đ ng
A. Hai đư ng th ng phân biệt c ng song song v i m t ph ng thì song song
v i nhau.
B. Hai m t ph ng phân biệt c ng song song v i một đư ng th ng thì song
song v i nhau.
C. Hai m t ph ng phân biệt h ng song song thì c t nhau.
D. Hai m t ph ng phân biệt c ng song song v i một m t ph ng thứ ba thì
song song v i nhau.
E. Một đư ng th ng c t một trong hai m t ph ng song song thì c t m t ph ng
c n lại.
Đáp án: C, D, E.
Để tr l i câu h i này thì h c sinh ph i bi t đư c vị tr tương đ i của đư ng
th ng v i đư ng th ng, đư ng th ng v i m t ph ng, m t ph ng v i m t ph ng,
bi t hệ qu trang 62 SGKHH11 NC, đinh l trang 1 nh lại i n thức và
th ng tin).
A.Sai .Từ định l ( trang SGKHH NC ta ch ra đư c tồn tại hai đư ng
th ng c t nhau c ng song song v i một m t ph ng.
B.Sai.Từ hệ qu trang ta ch ra đư c có hai m t ph ng c t nhau c ng
song song v i một đư ng th ng.
C.Đ ng. ị tr tương đ i của hai m t ph ng phân biệt song song, c t nhau).
5
D.Đ ng. Từ hệ qu trang .
E.Đ ng. ị tr tương đ i của đư ng th ng v i m t ph ng.
1.2.
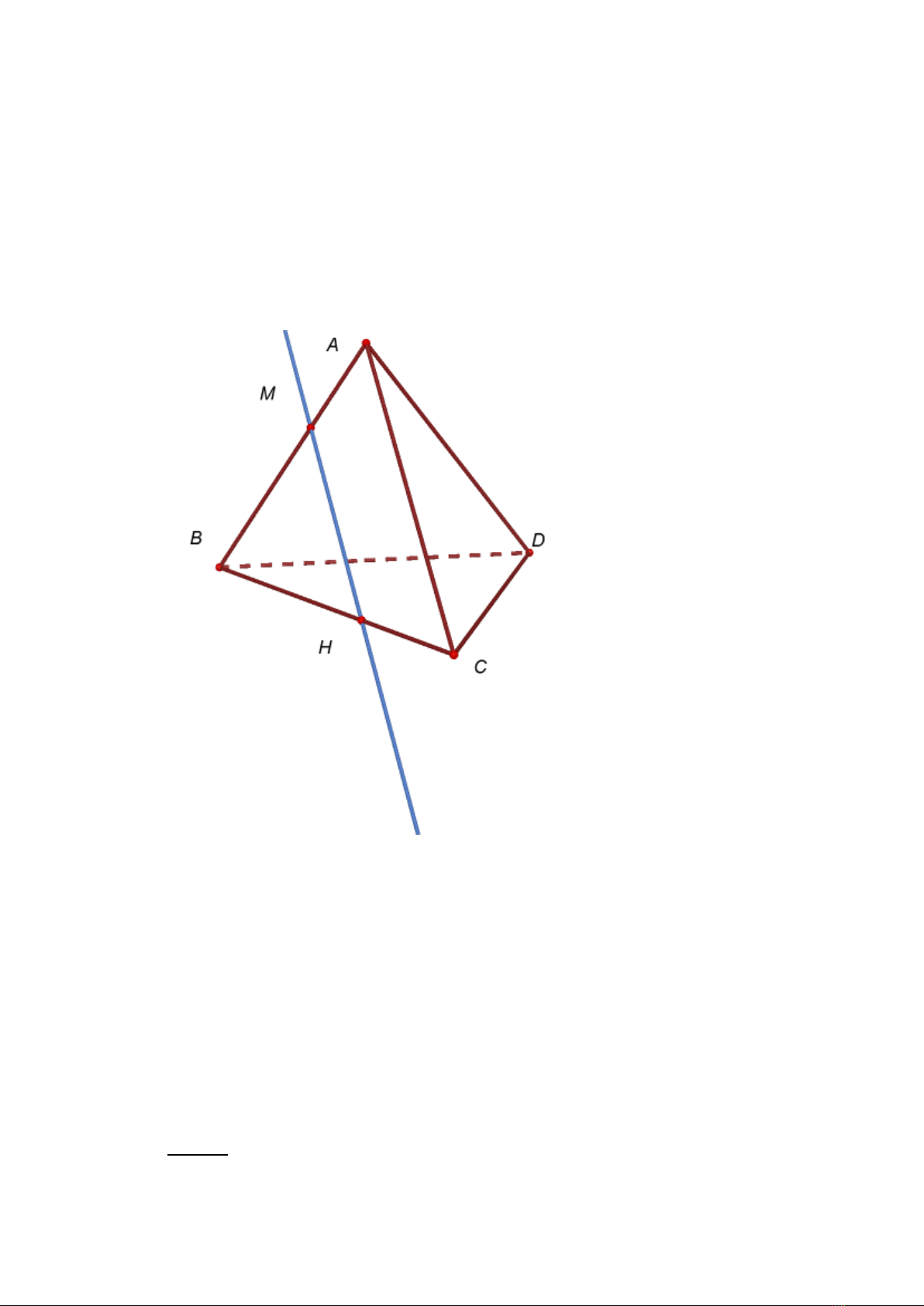
2: Cho bài toán ABCD. Trên cạnh AB l y điểm M, cho là m t
ph ng qua M và song song v i AC. Tìm giao tuy n của v i m t ph ng
(ABC).
Gi i:
Do AC mp(ABC) mà // AC nên giao tuy n của hai m t ph ng và
(ABC) song song v i AC.
Từ M kẻ (d)// AC. G i . Khi đó MH là giao tuy n cần tìm
Đâ l n bi t của h c sinh:
p dụng định l SGKHH -NC thì h c sinh s ch ra đư c giao tuy n của
hai m t ph ng ( va song song v i .
Do M n m trong m t ph ng và M thuộc m t ph ng ( nên M thuộc
giao tuy n t nh ch t thừa nhận 4 SGKHH 11- NC trang 43). Từ đó dựa vào
định ngh a hai đư ng th ng song song và t nh ch t thừa nhận 5 ta v đư c MH
như trên.
2. T u:
Ví dụ 3:
Cho hình chóp có đáy là hình bình hành.