TÝnh to¸n ®éng häc vµ m« pháng 3D r«bèt Gryphon
§inh V¨n Phong *, §ç Sanh *, NguyÔn Träng ThuÇn *, §ç §¨ng Khoa **
*Tr−êng §¹i häc B¸ch Khoa Hµ néi, **§Ò tµi 3.312.01
Tãm t¾t: Bµi b¸o ®Ò cËp ®Õn bµi to¸n ®iÒu khiÓn ®éng häc cña r«bèt vµ ¸p dông vµo
r«bèt Gryphon. Néi dung cña bµi b¸o nh»m gi¶i quyÕt bµi to¸n thuËn, bµi to¸n ng−îc vµ m«
pháng ho¹t ®éng cña r« bèt trong kh«ng gian ®å ho¹ ba chiÒu. §ång thêi trong bµi b¸o
còng giíi thiÖu h−íng nghiªn cøu viÖc ®iÒu khiÓn r« bèt Gryphon b»ng m¸y tÝnh.
1. Më ®Çu
Trong bµi b¸o nµy kh¶o s¸t bµi to¸n ®iÒu khiÓn ®éng häc r« bèt, chñ yÕu tËp trung
vµo hai bµi to¸n :
• Bµi to¸n thuËn : x¸c ®Þnh vÞ trÝ ®iÓm cuèi vµ h−íng tay kÑp mµ tay m¸y ®¹t ®−îc khi qui
luËt thay ®æi theo thêi gian cña c¸c th«ng sè ®Þnh vÞ cña tay m¸y lµ hµm ®· biÕt. Bµi
to¸n nµy nh»m phôc vô bµi to¸n x¸c ®Þnh ph¹m vi ho¹t ®éng cña tay m¸y, bµi to¸n
thuËn trong ®éng lùc häc tay m¸y….
• Bµi to¸n ng−îc : x¸c ®Þnh qui luËt thay ®æi theo thêi gian cña tay m¸y ®Ó nã n¾m b¾t
®−îc vÞ trÝ ®· cho cña ®èi t−îng theo mét h−íng ®Þnh tr−íc cña tay kÑp. Bµi to¸n nµy
nh»m phôc vô c¸c bµi to¸n ®iÒu khiÓn quÜ ®¹o, c¸c bµi to¸n ®iÒu khiÓn tèi −u...
Bµi b¸o d−íi ®©y sÏ tr×nh bµy c¬ së lý thuyÕt cña c¶ hai bµi to¸n vµ minh ho¹ qua viÖc ¸p
dông ®Ó m« pháng mét r« bèt cô thÓ.
2. C¬ së lý thuyÕt.
2.1 C«ng thøc x¸c ®Þnh vÞ trÝ
Trong bµi b¸o nµy chóng ta sÏ sö dông ph−¬ng ph¸p ma trËn Denavit-Hartenberg.
g¾n c¸c hÖ trôc täa ®é vµo tõng kh©u cña tay m¸y (r«bèt). Nhê ®ã mèi quan hÖ vÒ to¹ ®é
cña cïng mét ®iÓm trªn hai hÖ trôc kÕ tiÕp nhau sÏ ®−îc x¸c ®Þnh b»ng mét ma trËn chuyÓn
4x4.,xem tr 53 [3].
Gäi
j
j
-1
H lµ ma trËn chuyÓn to¹ ®é mét ®iÓm tõ hÖ j ( Oxjyjzj ) vÒ hÖ j-1 ( Oxj-1yj-1zj-1 ), ta
cã:
cos( ) cos( ).sin( ) sin( ).sin( ) .cos( )
sin( ) cos( ).cos( ) -sin( ).cos( ) .sin( )
0sin() cos()
00 0 1
jjj jjkj
jjj jjkj
jjj
a
a
d
θ
αθ αθ θ
θαθ αθ θ
αα
=
j
j-1
H (2.1)
trong ®ã c¸c tham sè cã ý nghÜa nh− sau:
• θj lµ gãc quay trôc xj-1 ®Õn trôc xj quanh trôc zj-1,
• dj lµ ®o¹n dÞch trôc xj-1 ®Õn trôc xj däc trôc zj-1,
• aj lµ ®o¹n dÞch trôc zj-1 ®Õn trôc zj däc trôc xj-1,
• αj lµ gãc quay trôc zj-1 ®Õn trôc zj quanh trôc xj-1.
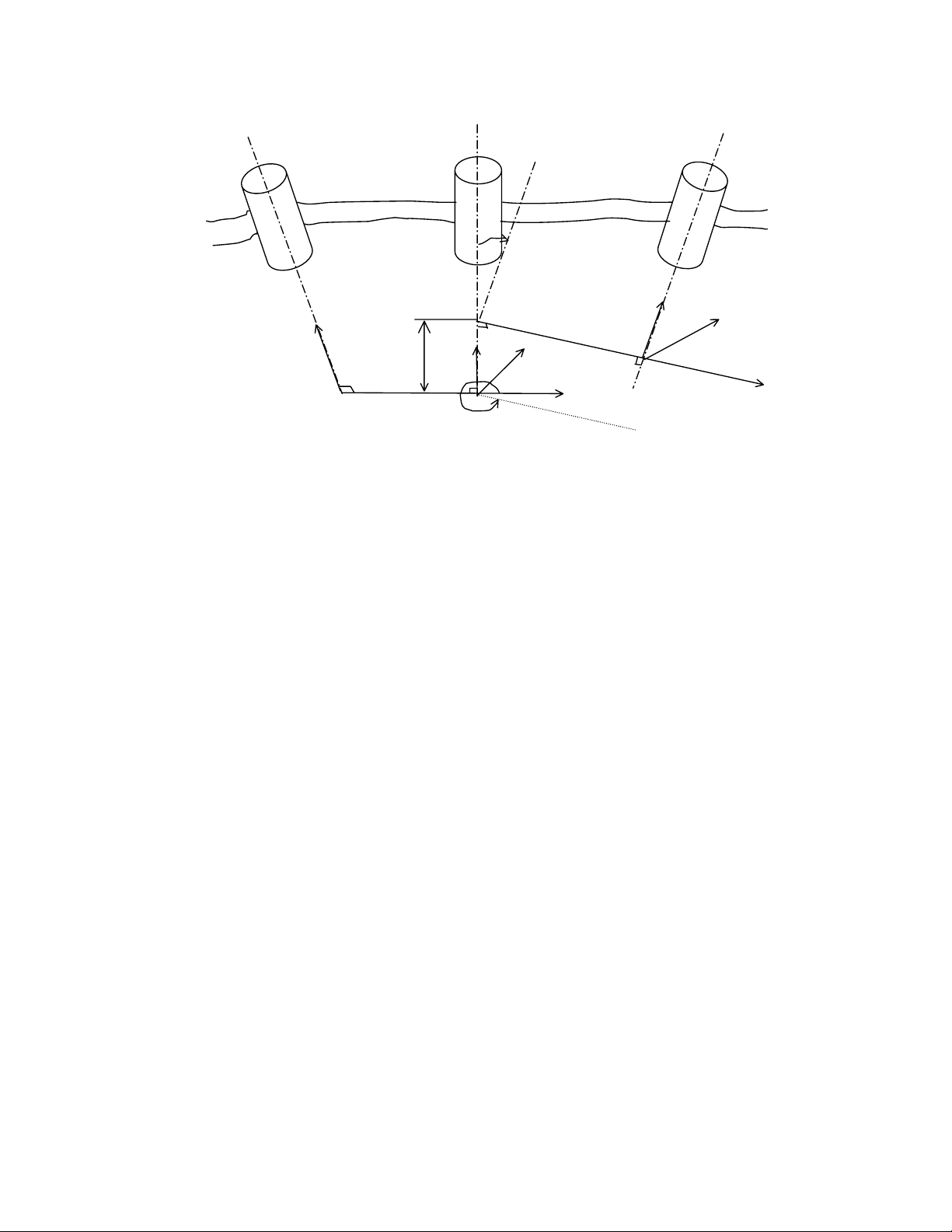
Th«ng qua viÖc sö dông liªn tiÕp c¸c hÖ to¹ ®é, ma trËn chuyÓn hÖ to¹ ®é g¾n vµo
tay kÑp vÒ hÖ to¹ ®é g¾n vµo ®Õ cña r« bèt cã d¹ng:
(
)
(
)
(
)
(
)
12 n
qq q
tay kep 1 2 n n
de 0 1 n-1 0
H = H .H ....H = H q
(
)
n
0
Hq
cã d¹ng:
(
)
(
)
1
Rq pq
0 (2.2)
trong ®ã hÖ to¹ ®é ®Õ r« bèt kÝ hiÖu lµ 0, hÖ to¹ ®é tay kÑp r« bèt kÝ hiÖu lµ n, q lµ ma trËn
nx1 cña c¸c to¹ ®é suy réng,chóng lµ c¸c th«ng sè ®Þnh vÞ cña r«bèt. R(q) lµ ma trËn 3x3
x¸c ®Þnh h−íng cña tay kÑp, p(q) lµ vect¬ 3x1 x¸c ®Þnh vÞ trÝ ®Çu bµn kÑp so víi hÖ ®Õ. Ba
cét cña ma trËn R t−¬ng øng víi h−íng cña ba vect¬ ®¬n vÞ trªn hÖ g¾n víi tay kÑp so víi
hÖ ®Õ r«bèt (hÖ to¹ ®é nÒn).
VÞ trÝ cña mét ®iÓm P thuéc tay kÑp ®−îc x¸c ®Þnh theo c«ng thøc :
(
)
0
n′
pp
r=H qr (2.3)
trong ®ã p
r lµ vect¬ ®Þnh vÞ ®iÓm P thuéc tay kÑp so víi hÖ to¹ ®é nÒn, ′p
r lµ vect¬ ®Þnh vÞ
®iÓm P trong hÖ to¹ ®é g¾n vµo tay kÑp r«bèt.
2.2 C«ng thøc x¸c ®Þnh vËn tèc.
Tõ c«ng thøc (2.3) ta dÔ dµng x¸c ®Þnh ®−îc vËn tèc ®iÓm P g¾n vµo tay kÑp r«bèt
so víi hÖ to¹ ®é nÒn :
′
pp np
0
v=r=H.r
&
& (2.4)
§Ó tiÕn hµnh ®iÒu khiÓn ho¹t ®éng cña tõng kh©u r«bèt, ta tiÕn hµnh biÓu diÔn ma
trËn n
0
H
& d−íi d¹ng sau :
∑
n
n(i)
0i
i=1
H= Hq
&& (2.5)
trong ®ã H(i) lµ ma trËn øng víi khíp i vµ chØ phô thuéc vµo biÕn khíp,
p
r
&lµ vÐc t¬ vËn tèc
cña ®iÓm cuèi tay kÑp so víi hÖ to¹ ®é nÒn, n
0
H
& lµ ma trËn ®¹o hµm cña ma trËn Denavit-
Kh©u
j
-2 Kh©u
j
-1 Kh©u
j
Kh©u
j
+1
zj-2
dj zj-1 yj-1
xj-1
θ
j
xj
yj
zj
aj
aj-1
xj
H×nh 1
zj
Khíp
j
-1 Khíp
j
Khíp
j
+1
α
j
Hartenberg gi÷a hÖ to¹ ®é nÒn víi hÖ to¹ ®é g¾n vµo tay kÑp, i
q
& lµ vËn tèc cña chuyÓn
®éng t¹i khíp thø i.
3. Kh¶o s¸t ®éng häc cña r« bèt Gryphon.
3.1 Giíi thiÖu m« h×nh vµ nguyªn t¾c ho¹t ®éng.
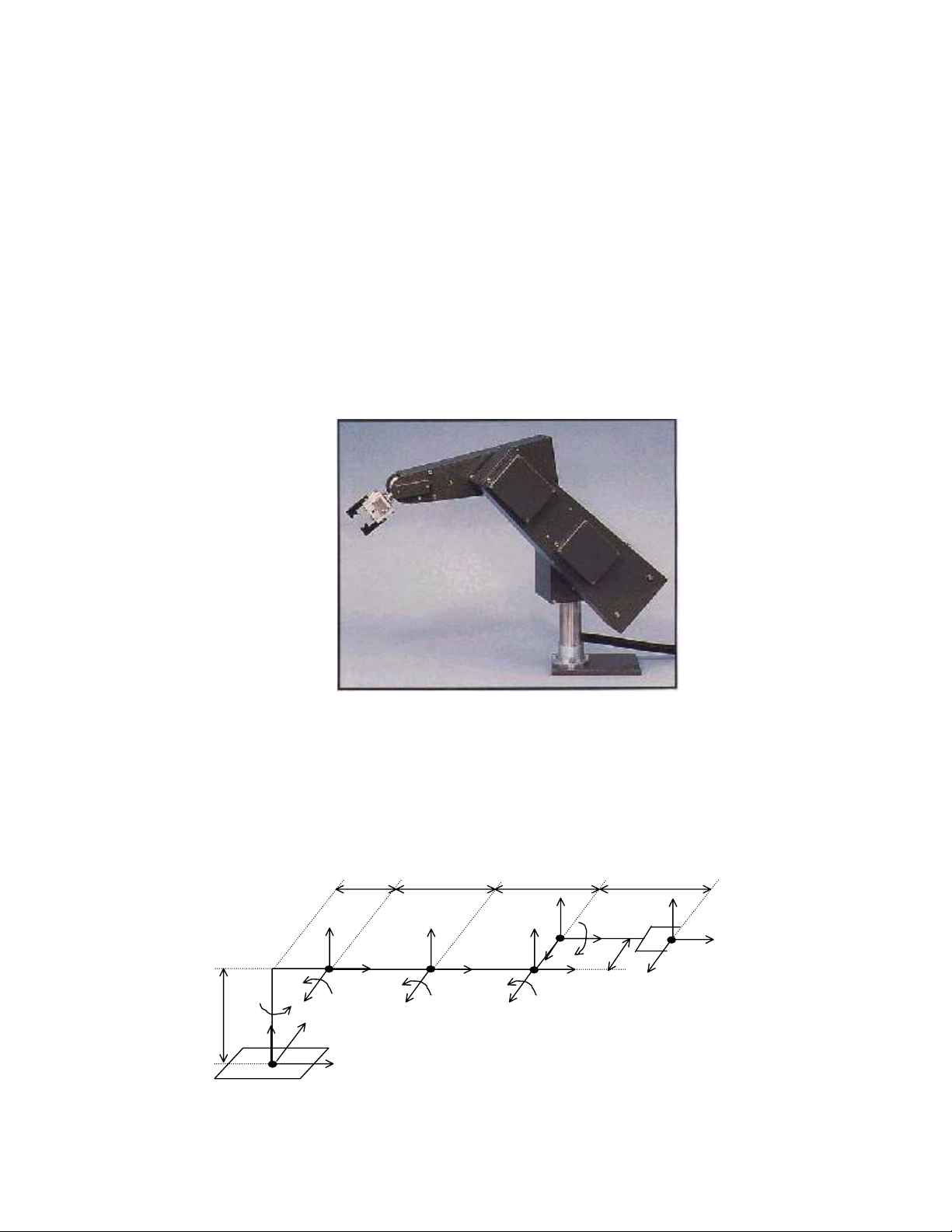
R« bèt Gryphon do h·ng FeedBack cña Anh s¶n xuÊt phôc vô cho môc ®Ých nghiªn
cøu. §©y lµ mét r«bèt n¨m trôc kÌm theo bµn kÑp nh− h×nh 2
• Trôc h«ng (waist axis).
• Trôc vai (shoulder axis).
• Trôc khuûu tay (elbow axis).
• Trôc cæ tay (tool pitch axis).
• Trôc cæ tay (tool roll axis).
• Bµn kÑp (gripper).
H×nh 2
Nh÷ng −u ®iÓm næi bËt cña r«bèt lµ chuyÓn ®éng nhanh, chÝnh x¸c vµ mÒm m¹i.
R«bèt ®−îc ®iÒu khiÓn bëi bèn vi xö lý cho phÐp ®iÒu khiÓn ®Æt vËt chÝnh x¸c. Mçi trôc cña
r«bèt ®−îc ®iÒu khiÓn bëi mét ®éng c¬ b−íc víi bé m· ho¸ ph¶n håi. Trong bé ®iÒu khiÓn,
mét vi xö lý sÏ gi¸m s¸t vÞ trÝ cña c¸c trôc. Hai c¸i kh¸c sÏ qu¶n lý c¸c ®éng c¬ vµ c¸i cßn
l¹i sÏ gi¸m s¸t c¶ ba c¸i trªn ®ång thêi lµm nhiÖm vô giao tiÕp víi m¸y chñ.
3.2 C«ng thøc x¸c ®Þnh vÞ trÝ
Khi ¸p dông ph−¬ng ph¸p Denavit-Hartenberg g¾n c¸c hÖ trôc to¹ ®é vµo c¸c kh©u
x
0
y
0
z
0
a1
θ
1
z
1
x1
y
1
a2 a4a
5
a
6
z
5
y
5
x
5
a
3
x4
y
4
z4
z
3
x
3
y
3
z2
θ
4
θ
5
θ
2
x2
y
2
θ
3
H×nh 3
ta thu ®−îc s¬ ®å ®éng häc cña r«bèt Gryphon nh− h×nh 3.
• B¶ng tham sè Denavit-Hartenberg:
Theo thuËt to¸n Denavit-Hartenberg ta cã b¶ng tham sè Denavit-Hartenberg øng
víi s¬ ®å ®éng häc trªn :
Trôc θ Dα a
1 θ1 a1 π/2 a2
2 θ2 00 a
4
3 θ3 00 a
5
4 θ4 -a3 π/2 0
5 θ5 a6 0 0
• X¸c ®Þnh c¸c ma trËn chuyÒn.
§©y lµ c¸c ma trËn chuyÓn thµnh chuyÓn c¸c hÖ to¹ ®é trªn s¬ ®å ®éng häc (h×nh 3).
1121
1121
1
0
0
01 0
00 0 1
CSaC
SCaS
a
−
=
1
0
H,
22 42
22 42
0
0
0010
0001
CS aC
SC aS
−
=
2
1
H,
33 53
33 53
0
0
0010
0001
CS aC
SC aS
−
=
3
2
H
,
44
44
3
00
00
01 0
00 0 1
CS
SC
a
−
=
−
4
3
H,
55
55
6
00
00
001
0001
CS
SC
a
−
=
5
4
H (3.1)
• Ma trËn chuyÓn toµn hÖ
ta
y
ke
p
de
H lµ ma trËn truyÒn thuÇn nhÊt gi÷a hÖ to¹ ®é nÒn vµ hÖ to¹ ®é g¾n vµo tay kÑp.
taykep 1 2 3 4 5
de 0 1 2 3 4
H =H.H.H.H.H
(
)
()
1 234 5 1 5 1 234 5 1 5 1 234 1 234 6 23 5 2 4 2 1 3
1 234 5 1 5 1 234 5 1 5 1 234 1 234 6 23 5 2 4 2 1 3
234 5 234 5 234 234 6 23 5 2 4 1
000 1
CC C SS CC S SC CS C S a C a C a a Sa
SC C CS SC S CC SS S S a C a Ca a Ca
SC SS C Ca Sa Sa a
+−+ +++−
−− − ++++
=
−−−+++
taykep
de
H
(3.2).
§Ó viÕt ®¬n gi¶n ta sö dông c¸c kÝ hiÖu sau: C1=cos(θ1), C234=cos(θ2+θ3+θ4), S1=sin(θ1),
S234=sin(θ2+θ3+θ4)….
• Ma trËn R
1 234 5 1 5 1 234 5 1 5 1 234
1 234 5 1 5 1 234 5 1 5 1 234
234 5 234 5 234
CC C SS CC S SC CS
SC C CS SC S CC SS
SC SS C
+− +
=−−−
−−
R (3.3)
• Vect¬ p
()
()
1 234 6 23 5 2 4 2 1 3
1 234 6 23 5 2 4 2 1 3
234 6 23 5 2 4 1
CS a Ca Ca a Sa
SSa Ca Ca a Ca
Ca Sa Sa a
+++−
=++++
−+++
p (3.4)
Xem [1].
3.3 Bµi to¸n thuËn
Ta cã thÓ x¸c ®Þnh vÞ trÝ vµ vËn tèc nh− sau:
Trong bµi to¸n thuËn
(
)
n
0
Hq tõ (2.3) lµ hµm ®· biÕt cña thêi gian, do ®ã ta tÝnh
®−îc
(
)
t=
pp
rr
Trong c«ng thøc (2.5) v×
(
)
(
)
,tt==qq qq
&& do ®ã (i)
H lµ hµm ®· biÕt cña t, tõ (2.4)
ta tÝnh ®−îc
(
)
t
pp
v=v .
3.4 Bµi to¸n ng−îc
3.4.1 Bµi to¸n vÞ trÝ
Môc ®Ých bµi to¸n nh»m x¸c ®Þnh c¸c gãc (1,5)
ii
θ
= ®Ó tay m¸y n¾m b¾t ®−îc ®èi
t−îng t¹i mét vÞ trÝ ®· cho vµ theo mét h−íng x¸c ®Þnh. Do ®ã d÷ liÖu vµo lµ vÞ trÝ ®Çu bµn
kÑp T
xyz
ppp
=
T
p vµ h−íng tay kÑp R.
Tõ c¸c c«ng thøc (3.3) vµ (3.4) ta nhËn thÊy r»ng cét thø 3 cña ma trËn R vµ p
kh«ng phô thuéc vµo θ5 mµ chØ phô thuéc vµo c¸c gãc θ1, θ2, θ3, θ4 do ®ã c¸c gãc nµy sÏ
®−îc x¸c ®Þnh theo vect¬ cÊu h×nh tay kÑp :
w=[px, py, pz, R13, R23, R33]. Nãi c¸ch kh¸c ta thu ®−îc hÖ ph−¬ng tr×nh sau:
(
)
()
1
12346 235 24 2 13
2
1 234 6 23 5 2 4 2 1 3
3
234 6 23 5 2 4 1
413
1234
523
1 234
633
234
w
w
w
ww
w
w
x
y
z
p
CS a Ca Ca a Sa
p
SSa Ca Ca a Ca
p
Ca Sa Sa a
R
CS
R
SS
R
C
+++−
++++
−+++
===
−
(3.5)
thùc hiÖn c¸c phÐp biÕn ®æi gi¶i tÝch, ta thu ®−îc kÕt qu¶ sau:
• Gãc quay ë khíp h«ng θ1 ®−îc tÝnh nh− sau
§Æt 222
123
wwba=± + −
1213123
atan2(w b-w a ,w b+w a )q⇒= (3.6)
• Gãc quay ë khíp khuûu θ3 ®ùoc tÝnh nh− sau:
(
)
(
)
1 1 13 1 2 13 1 2346 2
11 21 2346 2
2312346
ww
ww
w
bSaCCaSSaa
CSSaa
baCa
=+ +− − −
=+− −
=−+
víi 234 1 4 1 5 6
atan2( ,-w )qCwSw=+
2222
1245
3
45
2
bbaa
qaa
+−−
⇒=± (3.7)
• Gãc quay ë khíp vai θ2 ®−îc tÝnh nh− sau:
