http://ebook.here.vn Ti min phí ð thi, eBook, Tài liu hc tp
CHƯƠNG V
M(T S* BÀI TOÁN T*I ƯU TRÊN ð2 TH3
5.1. ð2 TH3 CÓ TR7NG S* VÀ BÀI TOÁN ðƯ8NG ðI NG9N NH:T.
5.1.1. M; ñ=u:
Trong ñi sng, chúng ta thưng gp nhng tình hung như sau: ñ ñi t ña
ñim A ñn ña ñim B trong thành ph, có nhi"u ñưng ñi, nhi"u cách ñi; có lúc ta
ch&n ñưng ñi ng'n nh(t (theo nghĩa c, ly), có lúc l/i c0n ch&n ñưng ñi nhanh nh(t
(theo nghĩa thi gian) và có lúc ph2i cân nh'c ñ ch&n ñưng ñi r4 ti"n nh(t (theo nghĩa
chi phí), v.v...
Có th coi sơ ñ9 c:a ñưng ñi t A ñn B trong thành ph là m;t ñ9 th, v<i ñ=nh
là các giao l; (A và B coi như giao l;), c/nh là ño/n ñưng ni hai giao l;. Trên m?i
c/nh c:a ñ9 th này, ta gán m;t s dương, Ang v<i chi"u dài c:a ño/n ñưng, thi gian
ñi ño/n ñưng hoc cư<c phí vBn chuyn trên ño/n ñưng ñó, ...
ð9 th có tr&ng s là ñ9 th G=(V,E) mà m?i c/nh (hoc cung) e∈E ñưHc gán bJi
m;t s th,c m(e), g&i là tr&ng s c:a c/nh (hoc cung) e.
Trong ph0n này, tr&ng s c:a m?i c/nh ñưHc xét là m;t s dương và còn g&i là
chi"u dài c:a c/nh ñó. M?i ñưng ñi t ñ=nh u ñn ñ=nh v, có chi"u dài là m(u,v), bOng
tPng chi"u dài các c/nh mà nó ñi qua. Kho2ng cách d(u,v) gia hai ñ=nh u và v là chi"u
dài ñưng ñi ng'n nh(t (theo nghĩa m(u,v) nhS nh(t) trong các ñưng ñi t u ñn v.
Có th xem m;t ñ9 th G b(t kỳ là m;t ñ9 th có tr&ng s mà m&i c/nh ñ"u có
chi"u dài 1. Khi ñó, kho2ng cách d(u,v) gia hai ñ=nh u và v là chi"u dài c:a ñưng ñi t
u ñn v ng'n nh(t, tAc là ñưng ñi qua ít c/nh nh(t.
5.1.2. Bài toán tìm ñưBng ñi ngDn nhEt:
Cho ñơn ñ9 th liên thông, có tr&ng s G=(V,E). Tìm kho2ng cách d(u
0
,v) t m;t
ñ=nh u
0
cho trư<c ñn m;t ñ=nh v b(t kỳ c:a G và tìm ñưng ñi ng'n nh(t t u
0
ñn v.
Có m;t s thuBt toán tìm ñưng ñi ng'n nh(t; J ñây, ta có thuBt toán do E.
Dijkstra, nhà toán h&c ngưi Hà Lan, ñ" xu(t năm 1959. Trong phiên b2n mà ta s` trình
bày, ngưi ta gi2 sa ñ9 th là vô hư<ng, các tr&ng s là dương. Ch= c0n thay ñPi ñôi chút
là có th gi2i ñưHc bài toán tìm ñưng ñi ng'n nh(t trong ñ9 th có hư<ng.
Phương pháp c:a thuBt toán Dijkstra là: xác ñnh tu0n t, ñ=nh có kho2ng cách
ñn u
0
t nhS ñn l<n.
Trư<c tiên, ñ=nh có kho2ng cách ñn a nhS nh(t chính là a, v<i d(u
0
,u
0
)=0. Trong
các ñ=nh v ≠ u
0
, tìm ñ=nh có kho2ng cách k
1
ñn u
0
là nhS nh(t. ð=nh này ph2i là m;t
trong các ñ=nh k" v<i u
0
. Gi2 sa ñó là u
1
. Ta có:
d(u
0,
u
1
) = k
1
.
http://ebook.here.vn Ti min phí ð thi, eBook, Tài liu hc tp
Trong các ñ=nh v ≠ u
0
và v ≠ u
1
, tìm ñ=nh có kho2ng cách k
2
ñn u
0
là nhS nh(t. ð=nh
này ph2i là m;t trong các ñ=nh k" v<i u
0
hoc v<i u
1
. Gi2 sa ñó là u
2
. Ta có:
d(u
0
,u
2
) = k
2
.
Tip tdc như trên, cho ñn bao gi tìm ñưHc kho2ng cách t u
0
ñn m&i ñ=nh v c:a G.
Nu V={u
0
, u
1
, ..., u
n
} thì:
0 = d(u
0
,u
0
) < d(u
0
,u
1
) < d(u
0
,u
2
) < ... < d(u
0
,u
n
).
5.1.3. Thut toán Dijkstra:
procedure Dijkstra (G=(V,E) là ñơn ñ9 th liên thông, có tr&ng s v<i tr&ng s dương)
{G có các ñ=nh a=u
0
, u
1
, ..., u
n
=z và tr&ng s m(u
i
,u
j
), v<i m(u
i
,u
j
) =
∞ nu (u
i
,u
j
) không là m;t c/nh trong G}
for i := 1 to n
L(u
i
) := ∞
L(a) := 0
S := V \ {a}
u := a
while S ≠ ∅
begin
for t(t c2 các ñ=nh v thu;c S
if L(u) +m(u,v) < L(v) then L(v) := L(u)+m(u,v)
u := ñ=nh thu;c S có nhãn L(u) nhS nh(t
{L(u): ñ; dài ñưng ñi ng'n nh(t t a ñn u}
S := S \ {u}
end
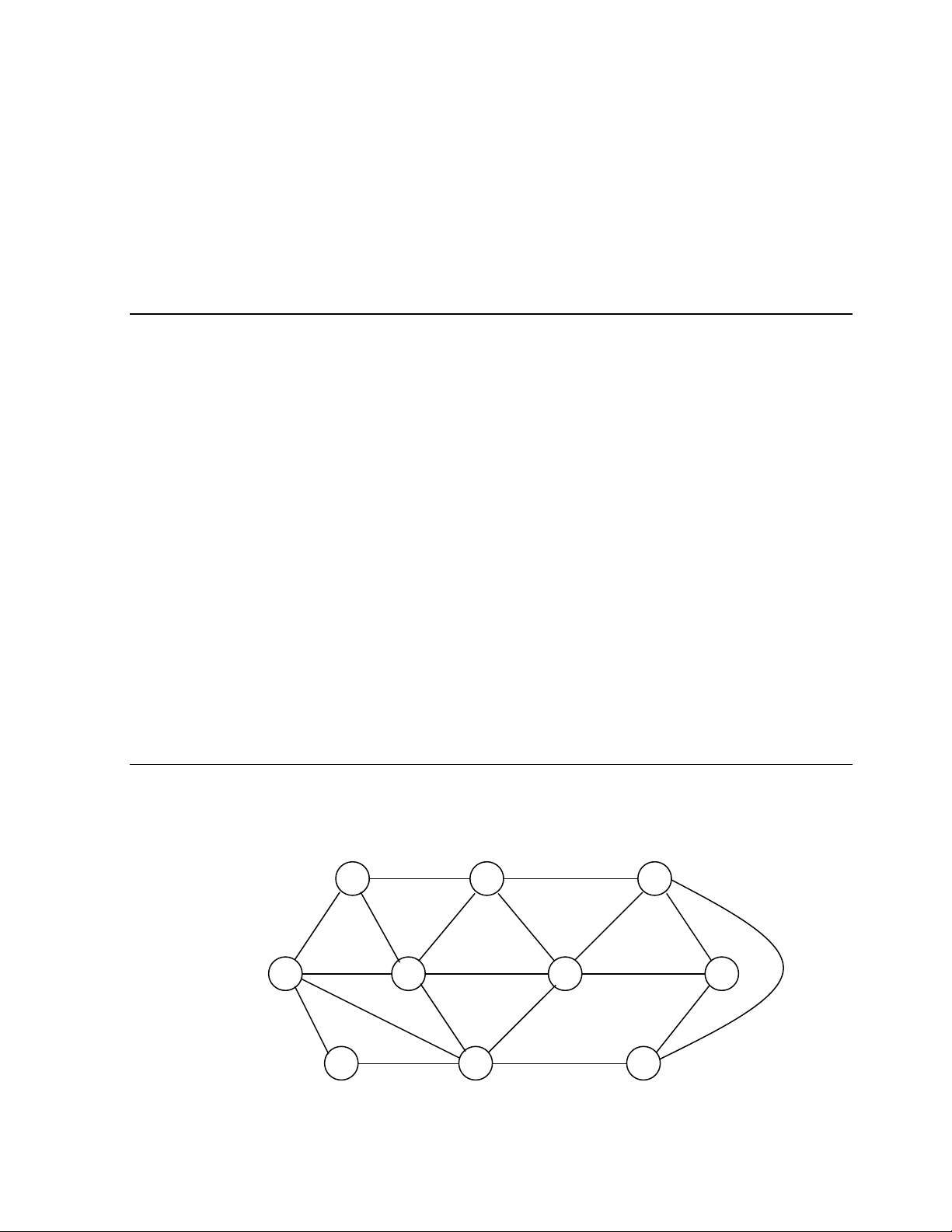
Thí dN 1: Tìm kho2ng cách d(a,v) t a ñn m&i ñ=nh v và tìm ñưng ñi ng'n nh(t t a
ñn v cho trong ñ9 th G sau.
a
n
b
e
d
g
m
c
h
k
1
3
3
2
1
4
2
4
2
6
2
3
5
5
6
3
1
2
3
http://ebook.here.vn Ti min phí ð thi, eBook, Tài liu hc tp
L(a) L(b) L(c) L(d) L(e) L(g) L(h) L(k) L(m) L(n)
5.1.4. ðPnh lý:
ThuBt toán Dijkstra tìm ñưHc ñưng ñi ng'n nh(t t m;t ñ=nh cho trư<c
ñn m;t ñ=nh tuỳ ý trong ñơn ñ9 th vô hư<ng liên thông có tr&ng s.
ChRng minh: ðnh lý ñưHc chAng minh bOng quy n/p. T/i bư<c k ta có gi2 thit quy
n/p là:
(i) Nhãn c:a ñ=nh v không thu;c S là ñ; dài c:a ñưng ñi ng'n nh(t t ñ=nh a t<i ñ=nh
này;
(ii) Nhãn c:a ñ=nh v trong S là ñ; dài c:a ñưng ñi ng'n nh(t t ñ=nh a t<i ñ=nh này và
ñưng ñi này ch= chAa các ñ=nh (ngoài chính ñ=nh này) không thu;c S.
Khi k=0, tAc là khi chưa có bư<c lp nào ñưHc th,c hirn, S=V \ {a}, vì th ñ; dài
c:a ñưng ñi ng'n nh(t t a t<i các ñ=nh khác a là ∞ và ñ; dài c:a ñưng ñi ng'n nh(t t
a t<i chính nó bOng 0 (J ñây, chúng ta cho phép ñưng ñi không có c/nh). Do ñó bư<c
cơ sJ là ñúng.
Gi2 sa gi2 thit quy n/p là ñúng v<i bư<c k. G&i v là ñ=nh l(y ra khSi S J bư<c
lp k+1, vì vBy v là ñ=nh thu;c S J cui bư<c k có nhãn nhS nh(t (nu có nhi"u ñ=nh có
nhãn nhS nh(t thì có th ch&n m;t ñ=nh nào ñó làm v). T gi2 thit quy n/p ta th(y rOng
0
∞
∞
∞
∞
∞
∞
∞
∞
∞
−
3
3
2
1
∞
∞
∞
∞
∞
−
−
5
2
2
∞
∞
∞
∞
3
−
−
−
3
2
5
∞
∞
∞
∞
−
−
−
−
4
6
3
∞
∞
∞
−
−
−
−
−
6
6
4
∞
∞
−
−
−
−
−
−
10
6
6
∞
−
−
−
−
−
−
−
9
6
8
−
−
−
−
−
−
−
7
8
−
−
−
−
−
−
−
−
−
−
8
http://ebook.here.vn Ti min phí ð thi, eBook, Tài liu hc tp
trư<c khi vào vòng lp thA k+1, các ñ=nh không thu;c S ñã ñưHc gán nhãn bOng ñ; dài
c:a ñưng ñi ng'n nh(t t a. ð=nh v cũng vBy ph2i ñưHc gán nhãn bOng ñ; dài c:a
ñưng ñi ng'n nh(t t a. Nu ñi"u này không x2y ra thì J cui bư<c lp thA k s` có
ñưng ñi v<i ñ; dài nhS hơn L
k
(v) chAa c2 ñ=nh thu;c S (vì L
k
(v) là ñ; dài c:a ñưng ñi
ng'n nh(t t a t<i v chAa ch= các ñ=nh không thu;c S sau bư<c lp thA k). G&i u là ñ=nh
ñ0u tiên c:a ñưng ñi này thu;c S. ðó là ñưng ñi v<i ñ; dài nhS hơn L
k
(v) t a t<i u
chAa ch= các ñ=nh không thu;c S. ði"u này trái v<i cách ch&n v. Do ñó (i) vvn còn ñúng
J cui bư<c lp k+1.
G&i u là ñ=nh thu;c S sau bư<c k+1. ðưng ñi ng'n nh(t t a t<i u chAa ch= các
ñ=nh không thu;c S s` hoc là chAa v hoc là không. Nu nó không chAa v thì theo gi2
thit quy n/p ñ; dài c:a nó là L
k
(v). Nu nó chAa v thì nó s` t/o thành ñưng ñi t a t<i
v v<i ñ; dài có th ng'n nh(t và chAa ch= các ñ=nh không thu;c S khác v, kt thúc bOng
c/nh t v t<i u. Khi ñó ñ; dài c:a nó s` là L
k
(v)+m(v,u). ði"u ñó chAng tS (ii) là ñúng vì
L
k+1
(u)=min(L
k
(u), L
k
(v)+m(v,u)).
5.1.5. Mnh ñ:
ThuBt toán Dijkstra tìm ñưng ñi ng'n nh(t t m;t ñ=nh cho trư<c ñn
m;t ñ=nh tuỳ ý trong ñơn ñ9 th vô hư<ng liên thông có tr&ng s có ñ; phAc t/p là O(n
2
).
ChRng minh: ThuBt toán dùng không quá n−1 bư<c lp. Trong m?i bư<c lp, dùng
không hơn 2(n−1) phép c;ng và phép so sánh ñ saa ñPi nhãn c:a các ñ=nh. Ngoài ra,
m;t ñ=nh thu;c S
k
có nhãn nhS nh(t nh không quá n−1 phép so sánh. Do ñó thuBt toán
có ñ; phAc t/p O(n
2
).
5.1.6. Thut toán Floyd:
Cho G=(V,E) là m;t ñ9 th có hư<ng, có tr&ng s. ð tìm ñưng ñi ng'n nh(t
gia m&i cp ñ=nh c:a G, ta có th áp ddng thuBt toán Dijkstra nhi"u l0n hoc áp ddng
thuBt toán Floyd ñưHc trình bày dư<i ñây.
Gi2 sa V={v
1
, v
2
, ..., v
n
} và có ma trBn tr&ng s là W ≡ W
0
. ThuBt toán Floyd xây
d,ng dãy các ma trBn vuông c(p n là W
k
(0 ≤ k ≤ n) như sau:
procedure Xác ñnh W
n
for i := 1 to n
for j := 1 to n
W[i,j] := m(v
i
,v
j
) {W[i,j] là ph0n ta dòng i c;t j c:a ma trBn W
0
}
for k := 1 to n
if W[i,k] +W[k,j] < W[i,j] then W[i,j] := W[i,k] +W[k,j]
{W[i,j] là ph0n ta dòng i c;t j c:a ma trBn W
k
}
5.1.7. ðPnh lý:
ThuBt toán Floyd cho ta ma trBn W*=W
n
là ma trBn kho2ng cách nhS
nh(t c:a ñ9 th G.
http://ebook.here.vn Ti min phí ð thi, eBook, Tài liu hc tp
ChRng minh: Ta chAng minh bOng quy n/p theo k mrnh ñ" sau:
W
k
[i,j] là chi"u dài ñưng ñi ng'n nh(t trong nhng ñưng ñi ni ñ=nh v
i
v<i ñ=nh
v
j
ñi qua các ñ=nh trung gian trong {v
1
, v
2
, ..., v
k
}.
Trư<c ht mrnh ñ" hin nhiên ñúng v<i k=0.
Gi2 sa mrnh ñ" ñúng v<i k•1.
Xét W
k
[i,j]. Có hai trưng hHp:
1) Trong các ñưng ñi chi"u dài ng'n nh(t ni v
i
v<i v
j
và ñi qua các ñ=nh trung gian
trong {v
1
, v
2
, ..., v
k
}, có m;t ñưng ñi γ sao cho v
k
∉ γ. Khi ñó γ cũng là ñưng ñi ng'n
nh(t ni v
i
v<i v
j
ñi qua các ñ=nh trung gian trong {v
1
, v
2
, ..., v
k•1
}, nên theo gi2 thit quy
n/p,
W
k•1
[i,j] = chi"u dài γ ≤ W
k•1
[i,k]+W
k•1
[k,j].
Do ñó theo ñnh nghĩa c:a W
k
thì W
k
[i,j]=W
k•1
[i,j].
2) M&i ñưng ñi chi"u dài ng'n nh(t ni v
i
v<i v
j
và ñi qua các ñ=nh trung gian trong
{v
1
, v
2
, ..., v
k
}, ñ"u chAa v
k
. G&i γ = v
i
... v
k
... v
j
là m;t ñưng ñi ng'n nh(t như th thì
v
1
... v
k
và v
k
... v
j
cũng là nhng ñưng ñi ng'n nh(t ñi qua các ñ=nh trung gian trong
{v
1
, v
2
, ..., v
k•1
} và
W
k•1
[i,k]+W
k•1
[k,j] = chi"u dài(v
1
... v
k
) + chi"u dài(v
k
... v
j
)
= chi"u dài γ < W
k•1
[i,j].
Do ñó theo ñnh nghĩa c:a W
k
thì ta có:
W
k
[i,j] = W
k•1
[i,k]+W
k•1
[k,j] .
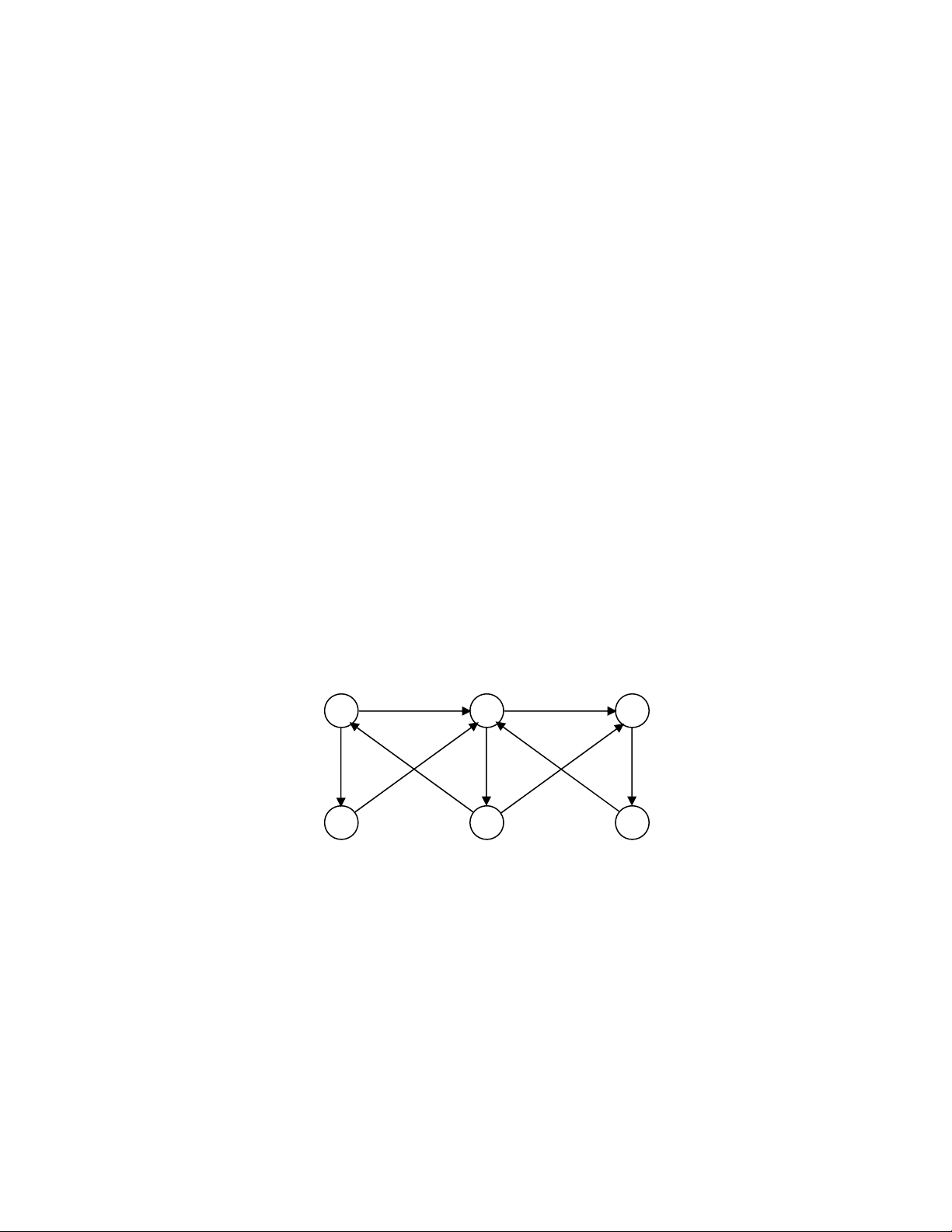
Thí dN 2: Xét ñ9 th G sau:
Áp ddng thuBt toán Floyd, ta tìm ñưHc (các ô trng là ∞)
W = W
0
=
1
22
4
3
14
27
v1
v2
v3
v4
v5
v6
4
7
2
2
4
1
1
2
3
![Bài giảng Toán rời rạc 1: Bài toán đếm - Ngô Xuân Bách [Mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2024/20241231/tambang1206/135x160/431735607183.jpg)
![Bài tập Đại số tuyến tính [chuẩn nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250930/dkieu2177@gmail.com/135x160/79831759288818.jpg)
