PHÒNG GD&ĐT HUYỆN ČƯ M’GAR
TRƯỜNG THCS NGÔ QUYỀN
KỲ THI CHỌN HỌC SINH GIỎI CẤP TRƯỜNG
NĂM HỌC 2017-2018
Khóa thi: Ngày 20/ 10/ 2017
MÔN: TOÁN 9
Thời gian: 120 phút (không kể thời gian giao đề)
Bài 1:(5 điểm ).
a) Phân tích đa thức sau thành nhân tử :
x5 + x4 + 1
b) Tìm các cặp các số nguyên x và y để cho
1 3
8 8
x
y
Bài 2: (4 điểm)
a, Chứng minh đa thức sau không có nghiệm:
4x2 + 4x + 5
b, Giải phương trình
3 4 1 8 6 1 5
x x x x
Câu 3: (7 điểm) Cho tam giác ABCvuông tại A, đường cao AH (H
BC).
Biết AB = 33cm , BC = 65cm.
a) Tính đường cao HC.
b) Chứng minh tam giác AHB đồng dạng tam giác CHA.
c) Gọi AE là phân giác của góc A( E
BC). Tính diện tích Tam giác AEB.
Bài 4: (2 điểm)
Cho tam giác ABC vuông tại A các đường trung tuyến AD và BE vuông góc tại G biết
AB =
18
. Tính cạnh huyền BC
Bài 5: (2 điểm).
Chứng minh A =
-----------------------------HẾT---------------------------
ĐỀ CHÍNH THỨC
PHÒNG GD&ĐT HUYỆN ČƯ M’GAR
TRƯỜNG THCS NGÔ QUYỀN
HƯỚNG DẪN CHẤM
KỲ THI CHỌN HỌC SINH GIỎI CẤP TRƯỜNG
NĂM HỌC 2017-2018
Khóa thi: Ngày 20/ 10/ 2017
MÔN: TOÁN 9
Thời gian: 120 phút (không kể thời gian giao đề)
Bài Câu Nội dung Điểm
Bài 1
5 điểm
a x
5
+ x
4
+ 1 =
= x5 + x4 + x3 - x3 + x2 - x2 + x - x +1
= (x5+x4+x3) -(x3+x2 +x) +(x2 +x+1)
= x3(x2 +x+1) - x(x2+x+1) + (x2 +x+ 1)
= (x2 + x +1) ( x3 - x +1)
1
0,5
0,5
0,5
b Điều kiện x
0
2 3
5 5
y
x
xy – 10 = 3x
xy – 3x = 10
x(y – 3) = 10 Suy ra x, y – 3là Ư(10)
Ư(10) =
1; 2; 5; 10
Xét bảng
x -1 1 - 2 2 - 5 5 - 10 10
y-3 -10 10 - 5 5 - 2 2 - 1 1
y -7 13 - 2 8 1 5 2 4
Vậy có 8 cặp số nguyên (x,y)thỏa mãn: (- 1;- 5); (1;13);
(- 2;-2); (2; 8); (-5; 1); (5; 5); (10; 2); (10; 4)
0,25
0,25
0,5
0,25
1,0
0,25
Bài 2
4 điểm
a 4x
2
+ 4x + 5 = (2x)
2
+ 2.2x + 1 + 4
(2x +1)2 + 4
Vì (2x +1)2
0 với mọi x
Nên (2x +1)2 + 4 > 0 với mọi x
Do đó f(x) không có nghiệm
0,5
0,25
0,25
0,25
0,25
b ĐKXĐ ta được x
1
3 4 1 8 6 1 5
x x x x
2 2
( 1 2) ( 1 3) 5
1 2 1 3 5
1 2 2 1
1 2 0
5
x x
x x
x x
x
x
Kết hợp với ĐKXĐ ta được 1
x
5
0,25
0,5
0,5
0,5
0,5
0,25
Bài 3
7 điểm
Vẽ hình ,ghi GT và KL đúng A
1
ĐỀ CHÍNH THỨC
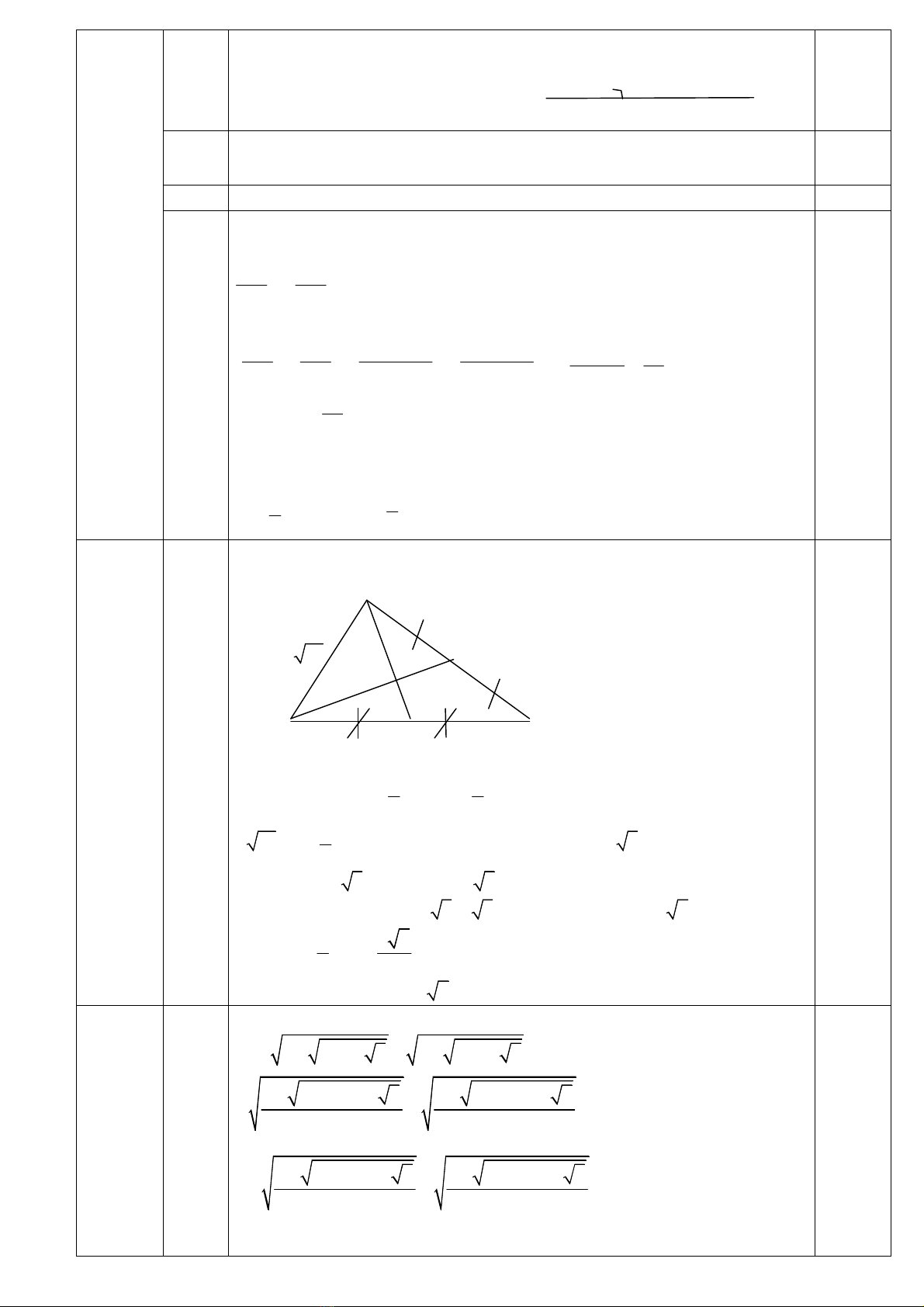
B H E C
a Tính được AC = 56cm
Tính được HC ≈ 48,246cm
1
1
b Chứng minh được tam giác AHB đồng dạng với tam giác CHA 1,5
C Áp dụng được tính chất đường phân giác trong của tam giác tính
được
EB
AB = EC
AC
Theo tính chất của dãy tỉ số bằng nhau suy ra:
EB
AB = EC
AC = EB+EC
AB+AC = BC
AB+AC =
65 65
33 56 89
EB =
65
89
. 33
24,101 (cm)
Ta có: AH.BC=AB.AC
AH=(AB.AC):BC
=(33.56):65
28,431(cm)
S =
2
1EB. AH
1
2 .24,101.28,431
342,608 (cm2 )
0,5
0,5
0,5
0,5
0,5
Bài 4
2 điểm
Vẽ hình ,ghi GT và KL đúng
A
18
E
G
B D C
Áp dụng hệ thức b2 = ab/ trong Δ vuôngABE ta có: AB2 =
BE.BG = BE.
2
3
BE =
2
3
BE2 (G là trọng tâm)
(
18
)2 =
2
3
BE2
BE2 = 27
BE = 3
3
(đv đ đ d)
BG = 2
3
; GE =
3
AG2 = BG.EG = 2
3
.
3
= 6
AG =
6
(đv đ đ d)
AD =
3 3 6
2 2
AG (đv đ đ d)
Do đó BC= 2AD = 3
6
(đv đ đ d)
0,5
0,25
0,25
0,25
0,25
0,5
Bài 5
2 điểm
Áp dụng công thức “căn phức tạp”
8 40 8 5 8 40 8 5
8 64 40 8 5 8 64 40 8 5
2 2
8 64 40 8 5 8 64 40 8 5
2 2
A
5
5
5
2
8 42 8 5 8 ( 2 5 2
2. 2.
2 2
12 4 5 ( 10 5) 10 2
5
.....................................*◊*................................
PHÒNG GD&ĐT HUYỆN ČƯ M’GAR
TRƯỜNG THCS NGÔ QUYỀN
KỲ THI HỌC SINH GIỎI CẤP TRƯỜNG
NĂM HỌC 2017-2018
Khóa thi: Ngày 20/ 10/ 2017
Môn: VẬT LÝ 9
Thời gian: 120 phút (không kể thời gian giao đề)
Bài 1: (2,0 điểm)
Một người đi xe đạp từ A đến B. Trên một phần ba quãng đường đầu đi với vận tốc v1 =
12km/h, phần quãng đường còn lại với vận tốc v2 nào đó. Biết rằng vận tốc trung bình
trên cả quãng đường là 9km/h. Hãy tính vận tốc v2.
Bài 1:(2,0điểm)
Một vật rắn ở nhiệt độ 1500C được thả vào một bình nước thì làm cho nhiệt độ của nước
tăng từ 200C đến 500C. Nếu cùng với vật trên ta thả thêm một vật như thế ở nhiệt độ
1000C thì nhiệt độ của lượng nước đó bằng bao nhiêu?
Giả thiết chỉ có sự trao đổi nhiệt giữa vật và nước, bỏ qua sự mất mát nhiệt của hệ.
Bài 3:(2,0 điểm)
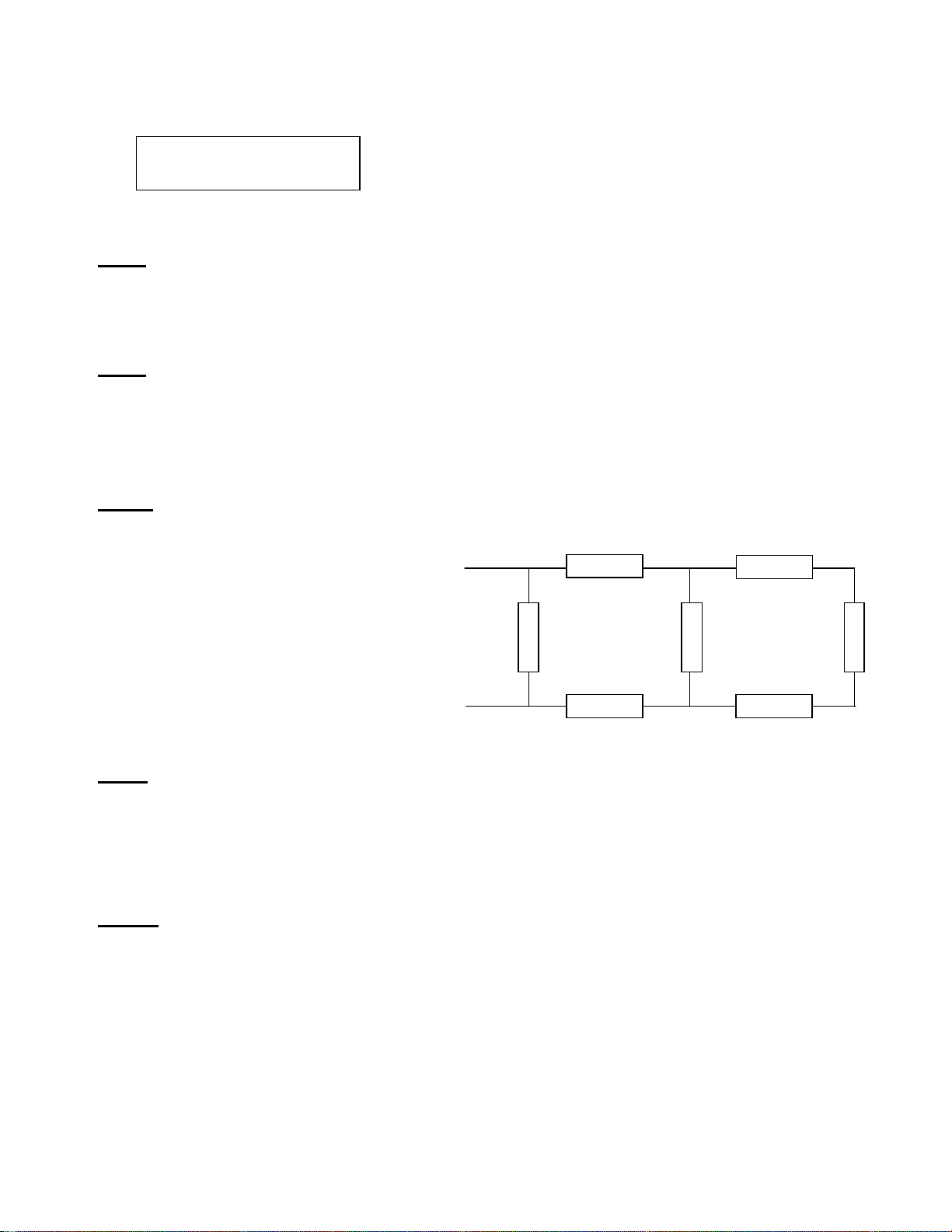
Cho mạch điện như hình vẽ:
Biết: R1 = 2R4 =8
, R2 = 3
, R3 =
5
, R7 = 2R6 = 4R5 = 24
. Cường
độ dòng điện mạch chính I =1A.
a,Tính hiệu điện thế hai đầu đoạn
mạch.
b, Tính cường độ dòng điện qua mỗi
điện trở.
Bài4:(2,0điểm)
Một mạch điện gồm một Am pe kế có điện trở RA, một điện trở R = 10
và một vôn kế
có điện trở RV = 1000
mắc nối tiếp. Đặt vào hai đầu đoạn mạch một hiệu điện thế U,
thì số chỉ của Vôn kế là 100V. Nếu mắc Vôn kế song song với điện trở R thì số chỉ của
nó vẫn là 100V. Tính RA và U.
Bài 5: (2,0điểm)
Xác định khối lượng riêng của một chất lỏng với các dụng cụ: Thước có vạch chia, giá thí
nghiệm và dây treo, một cốc nước đã biết khối lượng riêng Dn, một cốc có chất lỏng cần
xác định khối lượng riêng Dx, hai vật rắn khối lượng khác nhau có thể chìm trong các
chất lỏng nói trên.
-----------------------HẾT--------------------
1
R2
R
3
R
4
R
5
R
6
R
7
R
A
B
C
D
ĐỀ CHÍNH THỨC