TR NG THPT Đ NG THÚC H AƯỜ Ặ Ứ Đ KI M TRA S 1 - NĂM 2008Ề Ể Ố
GV: Tr n Đình Hi nầ ề Môn thi : Toán
Th i gian làm bài: 180 phútờ
Câu I: (2 đi m). Cho hàm s y = - xể ố 3 + 3mx2 -3m – 1.
1. Kh o sát s bi n thiên và v đ th c a hàm s khi m = 1.ả ự ế ẽ ồ ị ủ ố
2. Tìm các giá tr c a m đ hàm s có c c đ i, c c ti u. V i giá tr nào c a m thì đ th hàm s cóị ủ ể ố ự ạ ự ể ớ ị ủ ồ ị ố
đi m c c đ i, đi m c c ti u đ i x ng v i nhau qua đ ng th ng d: x + 8y – 74 = 0.ể ự ạ ể ự ể ố ứ ớ ườ ẳ
Câu II: (2 đi m).ể
1. Gi i ph ng trình : 1 + ả ươ
3
(sinx + cosx) + sin2x + cos2x = 0
2. Tìm m đ ph ng trình ể ươ
2 2
2
2 .( 4). 2 8 2 14 0
4
x
x x m x x x m
x
+
− + − + + − − − =
−
có nghi mệ
th c.ự
Câu III: (2 đi m).ể
Trong không gian v i h tr c to đ Đ các Oxyz, cho hai đ ng th ng ớ ệ ụ ạ ộ ề ườ ẳ ∆1 :
1 2 1
x y z
= =
−
,
∆2 :
1 1 1
1 1 3
x y z− + −
= =
−
1. Ch ng minh hai đ ng th ng ứ ườ ẳ ∆1 và ∆2 chéo nhau.
2. Vi t ph ng trình m t ph ng (P) ch a đ ng th ng ế ươ ặ ẳ ứ ườ ẳ ∆2 và t o v i đ ng th ng ạ ớ ườ ẳ ∆1 m t gócộ
300.
Câu IV: (2 đi m).ể
1. Tính tích phân :
2
3
2
1
ln( 1)x
I dx
x
+
==
.
2. Cho x, y, z > 0 và x + y + z ≤ xyz . Tìm giá tr l n nh t c a bi u th c.ị ớ ấ ủ ể ứ
2 2 2
1 1 1
2 2 2
Px yz y zx z xy
= + +
+ + +
Câu Va: (2 đi m).ể
1. Trong m t ph ng v i h to đ Đ các Oxy, cho tam giác ABC cân t i A , ph ng trình c nhặ ẳ ớ ệ ạ ộ ề ạ ươ ạ
AB: x + y – 3 = 0 , ph ng trình c nh AC : x – 7y + 5 = 0, đ ng th ng BC đi qua đi m M(1;ươ ạ ườ ẳ ể
10). Vi t ph ng trình c nh BC và tính di n tích c a tam giác ABC.ế ươ ạ ệ ủ
2. Tìm s h ng không ch a x trong khai tri n nh th c Niut n c a ố ạ ứ ể ị ứ ơ ủ
1
2.
n
xx
� �
+
� �
� �
, bi t r ngế ằ
2 1
1
4 6
n
n n
A C n
−
+
− = +
(n là s nguyên d ng, x > 0, ố ươ
là s ch nhh p ch p k c a n ph n t , ố ỉ ợ ậ ủ ầ ử
là s t h p ch p kố ổ ợ ậ
c a n ph n t )ủ ầ ử
………………. H t ……………….ế
1
ĐÁP ÁN Đ KI M TRA S 1 – GV: Tr n Đình Hi nỀ Ể Ố ầ ề
Câu N i dungộĐi mể
I-1 Khi m = 1. Ta có hàm s y = - xố3 + 3x2 – 4.
T p xác đ nh ậ ị D = R.
S bi n thiên.ự ế
Chi u bi n thiên.ề ế
y’ = - 3x2 + 6x , y’ = 0 ⇔ x = 0 v x = 2.
y’> 0 ∀ x ∈( 0;2). Hàm s đ ng bi n trên kho ng ( 0; 2).ố ồ ế ả
y’ < 0 ∀ x ∈(- ∞; 0) ∪ (2; +∞).Hàm s ngh ch bi n trên các kho ng (- ∞;0) và (2; +∞).ố ị ế ả
0,25
C c tr .ự ị Hàm s đ t c c đ i t i x = 2, yố ạ ự ạ ạ CĐ = y(2) = 0. Hàm s đ t c c ti u t i x = 0, yố ạ ự ể ạ CT = y(0) =
- 4.
Gi i h n.ớ ạ
3 2 3 2
( 3 4) , ( 3 4)
x x
Lim x x Lim x x
L−mx +L
− + − = +L− + − = −=
.Đ th hàm s không có ti mồ ị ố ệ
c n.ậ
0,25
Tính l i, lõm và đi m u n.ồ ể ố
y’’ = - 6x +6 , y’’ = 0 ⇔ x = 1.
x -∞ 1 +∞
y’’ + 0 -
Đ thồ ị
Lõm Đi m u nể ố L iồ
I(1; - 2) B ng bi nả ế
thiên.
x -∞ 0 1 2 +∞
y’ - 0 + 0 -
y +∞ 0
(I)
- 2
- 4 -∞
0,25
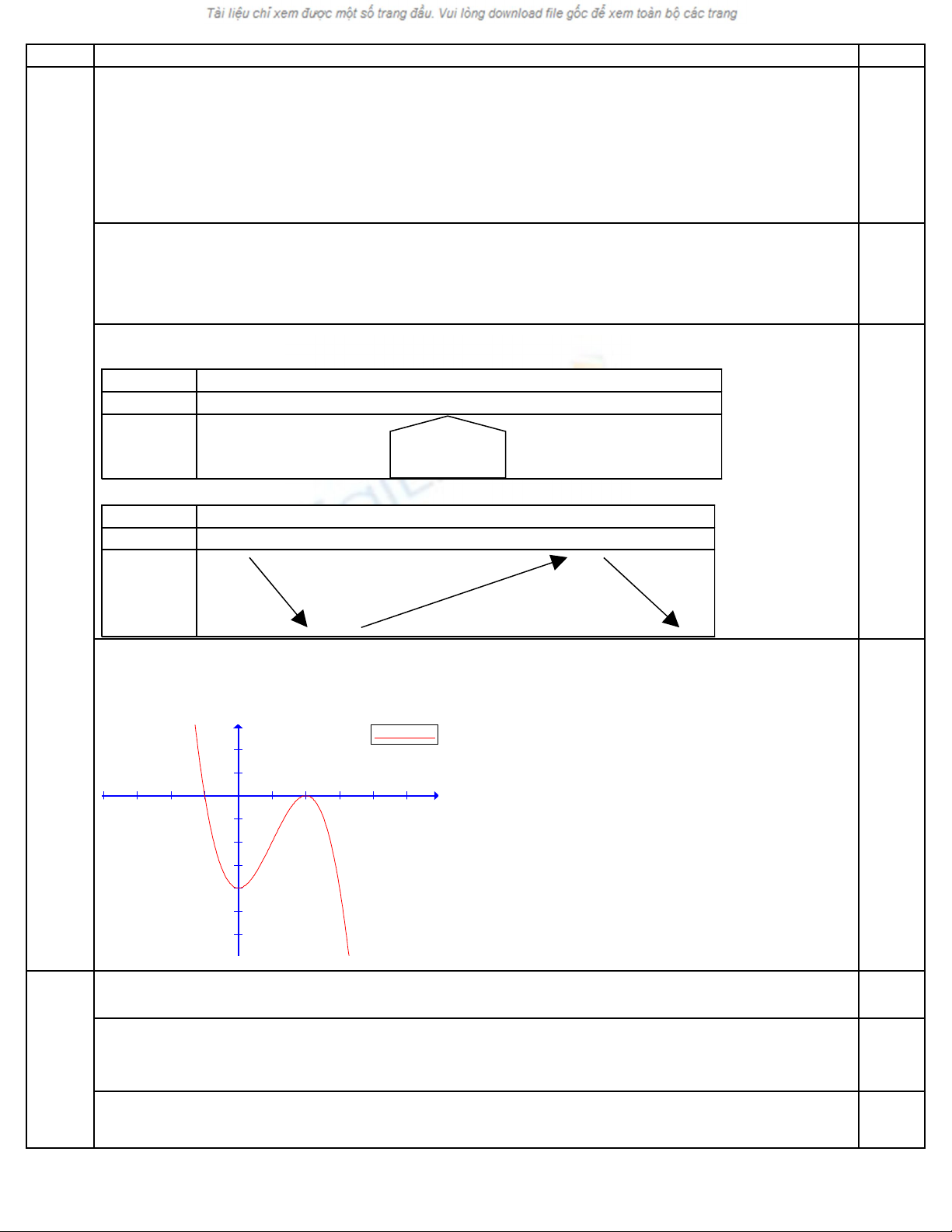
Đ th .ồ ị
Đ th hàm s c t tr c Ox tai các đi m (- 1; 0) , (2; 0). Đ th hàm s c t tr c Oy tai đi m (0 ;ồ ị ố ắ ụ ể ồ ị ố ắ ụ ể
-4). Đ th hàm s có tâm đ i x ng là đi m u n I(1;- 2).ồ ị ố ố ứ ể ố
H s góc c a ti p tuy n t i đi m u n là k = y’(1) = 3.ệ ố ủ ế ế ạ ể ố
f(x)=-x^3+3x^2-4
-3 -2 -1 1 2 3 4 5
-6
-5
-4
-3
-2
-1
1
2
x
y
0,25
I-2 Ta có y’ = - 3x2 + 6mx ; y’ = 0 ⇔ x = 0 v x = 2m.
Hàm s có c c đ i , c c ti u ố ự ạ ự ể ⇔ ph ng trình y’ = 0 có hai nghi m phân bi t ươ ệ ệ ⇔ m ≠ 0. 0,25
Hai đi m c c tr là A(0; - 3m - 1) ; B(2m; 4mể ự ị 3 – 3m – 1)
Trung đi m I c a đo n th ng AB là I(m ; 2mể ủ ạ ẳ 3 – 3m – 1)
Vect ơ
3
(2 ;4 )AB m m=
uuur
; M t vect ch ph ng c a đ ng th ng d là ộ ơ ỉ ươ ủ ườ ẳ
(8; 1)u= −
r
.
0,25
Hai đi m c c đ i , c c ti u A và B đ i x ng v i nhau qua đ ng th ng d ể ự ạ ự ể ố ứ ớ ườ ẳ ⇔
I d
AB d
A
A
A⊥
⊥
0,25
2
⇔
3
8(2 3 1) 74 0
. 0
m m m
AB u
A+ − − − =
+
+=
=
=
uuur r
⇔ m = 2 0,25
3
II-1 T p xác đ nh ậ ị D = R.
Ph ng trình đã cho t ng đ ng v i ươ ươ ươ ớ
( 3 s inx sin 2 ) 3 cos (1 os2 ) 0x x c x
� �
+ + + + =
� �
0,25
⇔
2
( 3 s inx 2sinx.cos ) ( 3 cos 2 os ) 0x x c x+ + + =
⇔
sinx( 3 2cos ) cos ( 3 2cos ) 0x x x+ + + =
0,25
⇔
( 3 2cos )(sinx cos ) 0x x+ + =
⇔
3
cos 2
sinx cos
x
x
x= −
=
== −
=
=
0,25
⇔
5
56
6
4
2
2 ,
t anx 1
x k
x k k Z
x k
π
π
π
π
π
π
π=k+
==
=k+
=� �
�
��
= − = − +
==
=
0,25
II-2
Đi u ki n:ề ệ
2
20
4
4 2 4
8 2 0
x
x
x x
x x
+
++
+−
−− <� � �
�
�+ −0
+
+
0,25
Ph ng trình đã cho t ng đ ng v i ươ ươ ươ ớ
2 2
2
2 | 4 | 2. 8 2 14 0
4
x
x x m x x x m
x
+
− − − + + − − − =
−
⇔
2 2 2
( 2 8) 8 2 2 8 2 6 0x x m x x x x m− − + + − + − + + − − − =
. (1)
Đ t t = ặ
2
8 2x x+ −
; Khi x ∈ [ - 2; 4) thì t ∈ [ 0; 3] . (2)
Ph ng trình tr thành : - tươ ở 2 – mt + 2t – 6 – m = 0 ⇔
2
2 6
1
t t
mt
− + −
=+
.
0,25
Xét hàm s ố
[ ]
2
2 6
( ) ; 0;3
1
t t
f t t
t
− + −
=+ +
; f’(t) =
2
2
2 8
( 1)
t t
t
− − +
+
; f’(t) = 0 ⇔ t = - 4 v t = 2.
B ng bi n thiên c a hàm s f(t) trên đo n ả ế ủ ố ạ [ 0 ; 3 ].
t -∞ -4 -1 0 2 3 +∞
f’(t) - 0 + + + 0 -
f(t)
- 2
-6
9
4
−
0,25
Ph ng trình đx cho có nghi m x ươ ệ ∈ [ - 2; 4) ⇔ Ph ng trình (2) có nghi m t ươ ệ ∈ [ 0; 3 ]
⇔ Đ ng th ng y = m c t đ th hàm s f(t) , t ườ ẳ ắ ồ ị ố ∈ [ 0; 3 ] ⇔ - 6 ≤ m ≤ - 2 0,25
III-1 Đ ng th ng ườ ẳ ∆1 có m t vect ch ph ng ộ ơ ỉ ươ
1
(1; 2;1)u= −
uur
, Đi m M ể≡ O(0; 0; 0) ∈ ∆1.0,25
Đ ng th ng ườ ẳ ∆2 có m t vect ch ph ng ộ ơ ỉ ươ
2
(1; 1;3)u= −
uur
, đi m N(1;-1;1) ể∈ ∆2.0,25
Ta có
1 2
2 1 1 1 1 2
, ; ; ( 5; 2;1)
1 3 3 1 1 1
u u − −� �
� �
= = − −
� �
� � − −
� �
uur uur
;
(1; 1;1)ON = −
uuur
. 0,25
Ta có
1 2
, . 5 2 1 2 0u u ON
� � = − + + = −0
� �
uur uur uuur
. Suy ra hai đ ng th ng ườ ẳ ∆1 và ∆2 chéo nhau. 0,25
III -2 Ph ng trình đ ng th ng ươ ườ ẳ ∆2 :
0
3 2 0
x y
y z
+ =
+
++ + =
+
.0,25
4
Ph ng trình m t ph ng (P) ch a đ ng th ng ươ ặ ẳ ứ ườ ẳ ∆2 có d ngạ
λ(x + y) + µ(3y + z + 2) = 0 v i ớλ2 + µ2 ≠ 0 ⇔ λx + (λ + 3µ)y + µz + 2µ = 0.
M t vect pháp tuy n c a m t ph ng (P) là ộ ơ ế ủ ặ ẳ
( ; 3 ; )n
λ λ µ µ
= +
r
.
0,25
M t ph ng (P) t o v i đ ng th ng ặ ẳ ạ ớ ườ ẳ ∆1 m t góc 30ộ0. Ta có sin(∆1,(P)) =
1
| os( , ) |c u n
uur r
⇔ sin300 =
2 2 2
|1. 2( 3 ) 1. |
6. ( 3 )
λ λ µ µ
λ λ µ µ
− + +
+ + +
⇔
2 2
3. 3 5 | 5 |
λ λµ µ λ µ
+ + = − −
0,25
⇔ 2λ2 - λµ - 10µ2 = 0 ⇔ (2λ - 5µ)(λ + 2µ) = 0 ⇔ 2λ = 5µ v λ = - 2µ
V iớ 2λ = 5µ ch n ọλ = 5, µ = 2 ta có ph ng trình m t ph ng (P) là: 5x + 11y + 2z + 4 = 0ươ ặ ẳ
V iớ λ = - 2µ ch n ọλ = 2, µ = - 1 ta có ph ng trình m t ph ng (P) là: 2x – y – z – 2 = 0.ươ ặ ẳ
K t lu n:ế ậ Có hai ph ng trình m t ph ng (P) tho mãn 5x + 11y + 2z + 4 = 0 ; 2x – y – z – 2 =ươ ặ ẳ ả
0.
0,25
IV-1
Đ t ặ
2
2
32
2
ln( 1) 1
1
2
x
du
u x x
dx
dv v
xx
x
x=
= + =
� � +
+
� �
=
� � = −
==
=
0,25
Do đó I =
2
2
2 2
1
2
ln( 1)
1
2 ( 1)
x dx
x x x
+
− + +
+
0,25
2
2
1
ln 2 ln 5 1
2 8 1
xdx
xx
� �
= − + −
� �
+
� �
�
2 2 2
2
1 1
ln 2 ln 5 1 ( 1)
2 8 2 1
dx d x
xx
+
= − + − +
� �
0,25
2
2
ln 2 ln 5 1
ln | | ln | 1| 1
2 8 2
x x
� �
= − + − +
� �
� �
=
5
2ln 2 ln 5
8
−
0,25
IV -2 T gi thi t ta có xyz ≥ x + y + z ≥ ừ ả ế
3
3xyz
⇔ (xyz)3 ≥ 27.xyz ⇔ xyz ≥ 3
3
.0,25
Áp d ng BĐT Cauchy ta có ụ
x2 + yz + yz ≥
2
3
3 ( )xyz
; y2 + zx + zx ≥
2
3
3 ( )xyz
; z2 + xy + xy ≥
2
3
3 ( )xyz
0,25
T đó ta có P ừ
2 2 2 2 2
3 3 3 3 3
1 1 1 1 1 1
3
3 ( ) 3 ( ) 3 ( ) ( ) (3 3)
xyz xyz xyz xyz
x+ + =y=
0,25
T đó ta có Max P = ừ
1
3
đ t đ c khi ạ ượ
3
x y z x y z
x y z xyz
= =
== = =�
�+ + =
+
.0,25
Va-1 To đ đi m A là nghi m c a h ph ng trình: ạ ộ ể ệ ủ ệ ươ
3 0 2
7 5 0 1
x y x
x y y
+ − = =
� �
�
� �
− + = =
� �
.Hay A(2;1)
Ph ng trình đ ng phân giác góc A là ươ ườ
3 7 5
2 5 2
x y x y
+ − − +
=−
⇔
1
2
3 5 0
3 5 0
d
x y
d
x y
+ − =
+
+− − =
−
0,25
Do tam giác ABC cân t i A nên đ ng phân giác trong k t A cũng là đ ng cao.ạ ườ ẻ ừ ườ
* N u dế1 là đ ng cao c a tam giác ABC k t A thì ph ng trình c nh BC là 3x – y + 7 = 0ườ ủ ẻ ừ ươ ạ
* N u dế2 là đ ng cao c a tam giác ABC k t A thì ph ng trình c nh BC là x + 3y - 31 = 0ườ ủ ẻ ừ ươ ạ 0,25
TH1: Ph ng trình c nh BC: 3x – y + 7 = 0ươ ạ
To đ đi m B là nghi m c a h ph ng trình ạ ộ ể ệ ủ ệ ươ
3 0 1
3 7 0 4
x y x
x y y
+ − = = −
� �
�
� �
− + = =
� �
. Hay B(-1; 4)
To đ đi m C là nghi m c a h ph ng trình ạ ộ ể ệ ủ ệ ươ
11
5
2
5
7 5 0
3 7 0
x
x y
x y y
y=−
=
− + =
−−
−
� �
−+=
−−=
=
=
. Hay C(
11 2
5 5
;−
)
Di n tích tam giác ABC là : ệ
1 1 24 36
( , ). . .3 2
2 2 5
5 2
S d C AB AB
= = =
(đvdt)
0,25
5