Ch−¬ng 6: Uèn ngang ph¼ng thanh th¼ng
1. Kh¸i niÖm chung
1.1. Kh¸i niÖm
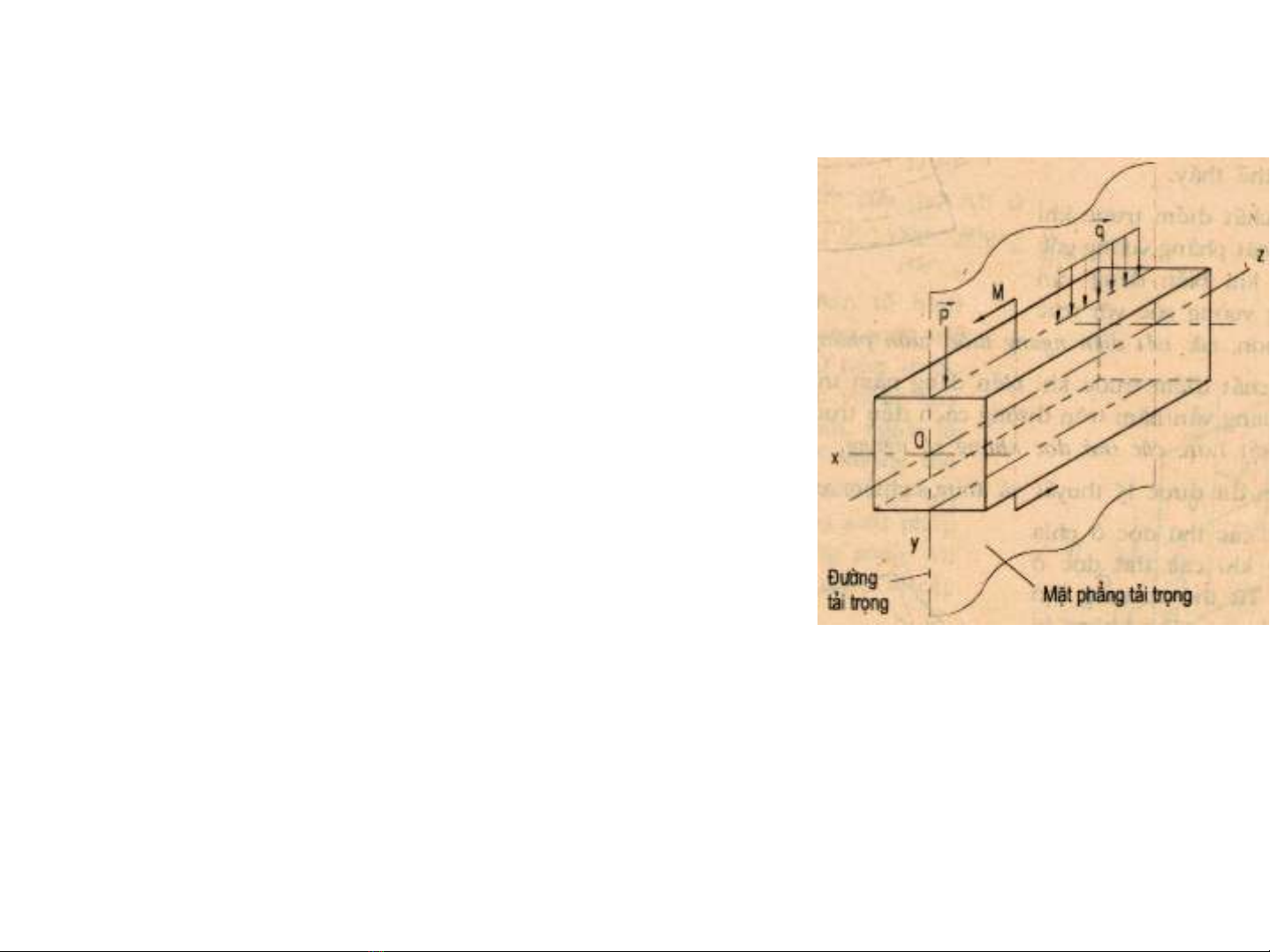
- Thanh chÞu uèn ngang ph¼ng;
- MÆt ph¼ng t¶i träng;
-§−êng t¶i träng;
- MÆt ph¼ng qu¸n tÝnh chÝnh trung t©m
- Thanh chÞu uèn thuÇn tuý.
1.2. BiÓu ®å néi lùc
-BiÓu ®å cña Mx, QyhoÆc My, Qx
-Sö dông ph−¬ng ph¸p mÆt c¾t
NhËn xÐt
- N¬i cã lùc tËp trung ⇒BiÓu ®å Qy, Mx;
- N¬i cã M« men uèn tËp trung;
-N¬i cã dμn lùc ph©n bè ®Òu.
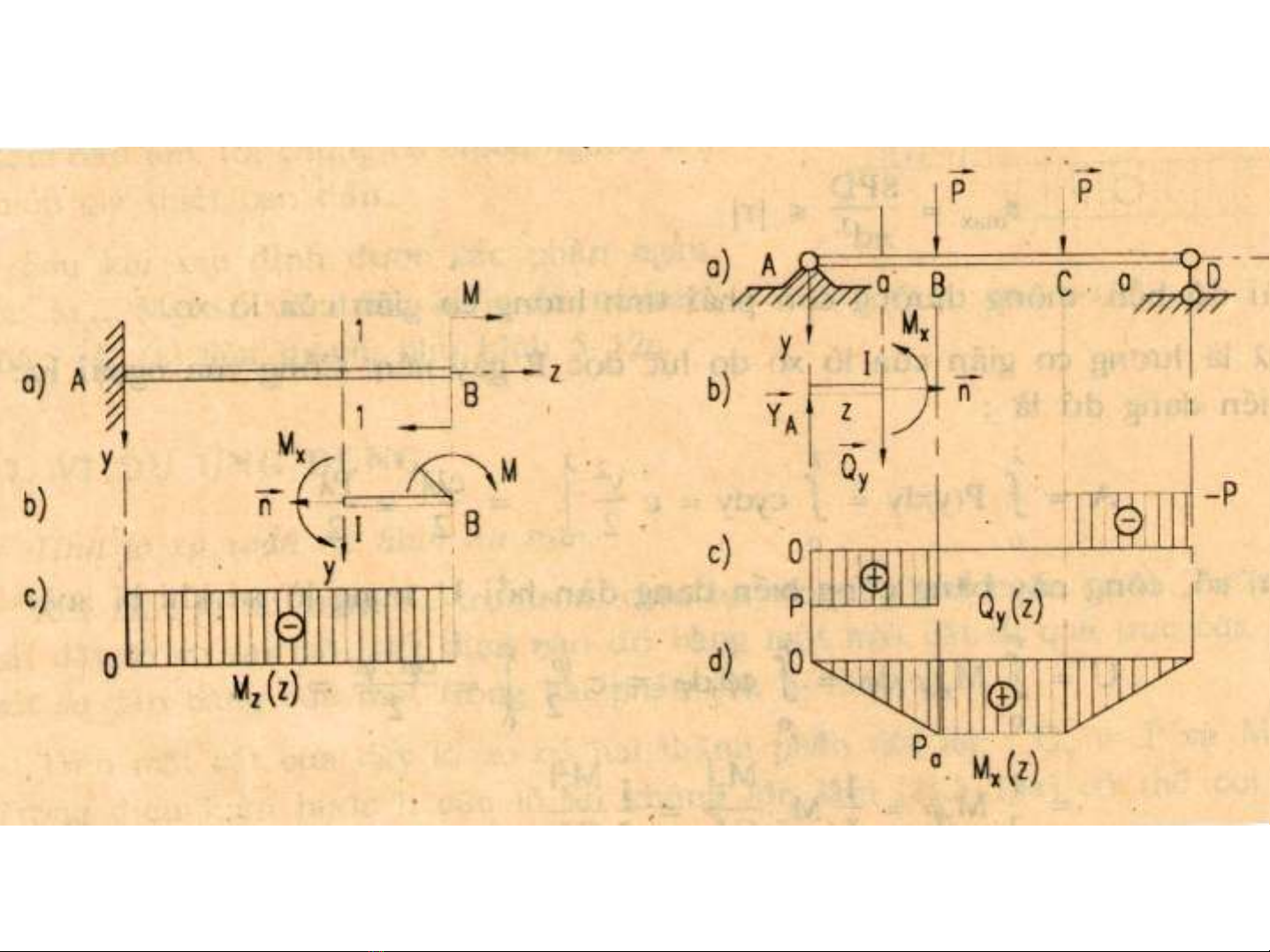
VÝ dô:
2. Uèn thuÇn tuý thanh th¼ng
2.1. øng suÊt
2.1.1. ThÝ nghiÖm
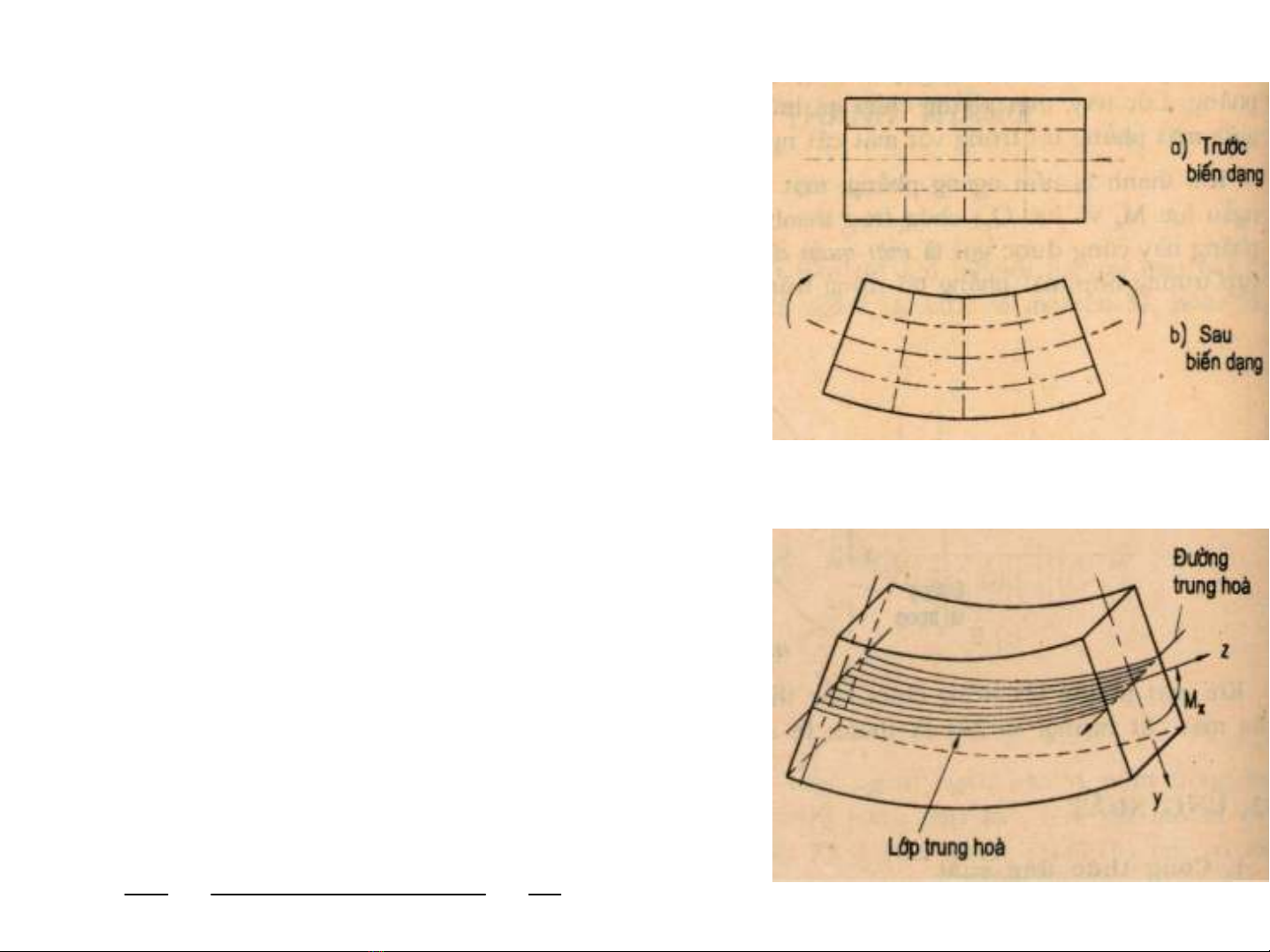
-KÎl−íi « h×nh ch÷ nhËt hoÆc vu«ng;
- T¸c dông m« men uèn ngo¹i lùc;
- C¸c mÆt c¾t ngang vÉn ph¼ng vμ
vu«ng gãc víi trôc cña thanh;
- C¸c thí däc kh«ng bÞ x« ngang.
2.1.2. §Æc ®iÓm biÕn d¹ng
- PhÇn co vμgi·n;
- Thí trung hoμvμlíp trung hoμ;
-§−êng trung hoμ-trôc trung hoμ;
-TÝnh l−îng biÕn d¹ng:
ϕ
ρ
ddz =
()
ϕ
ρ
δ
dyzdz +=+
()
ρϕρ
ϕ
ρ
ϕ
ρ
δ
ε
y
d
ddy
dz
z
z=
−
+
==
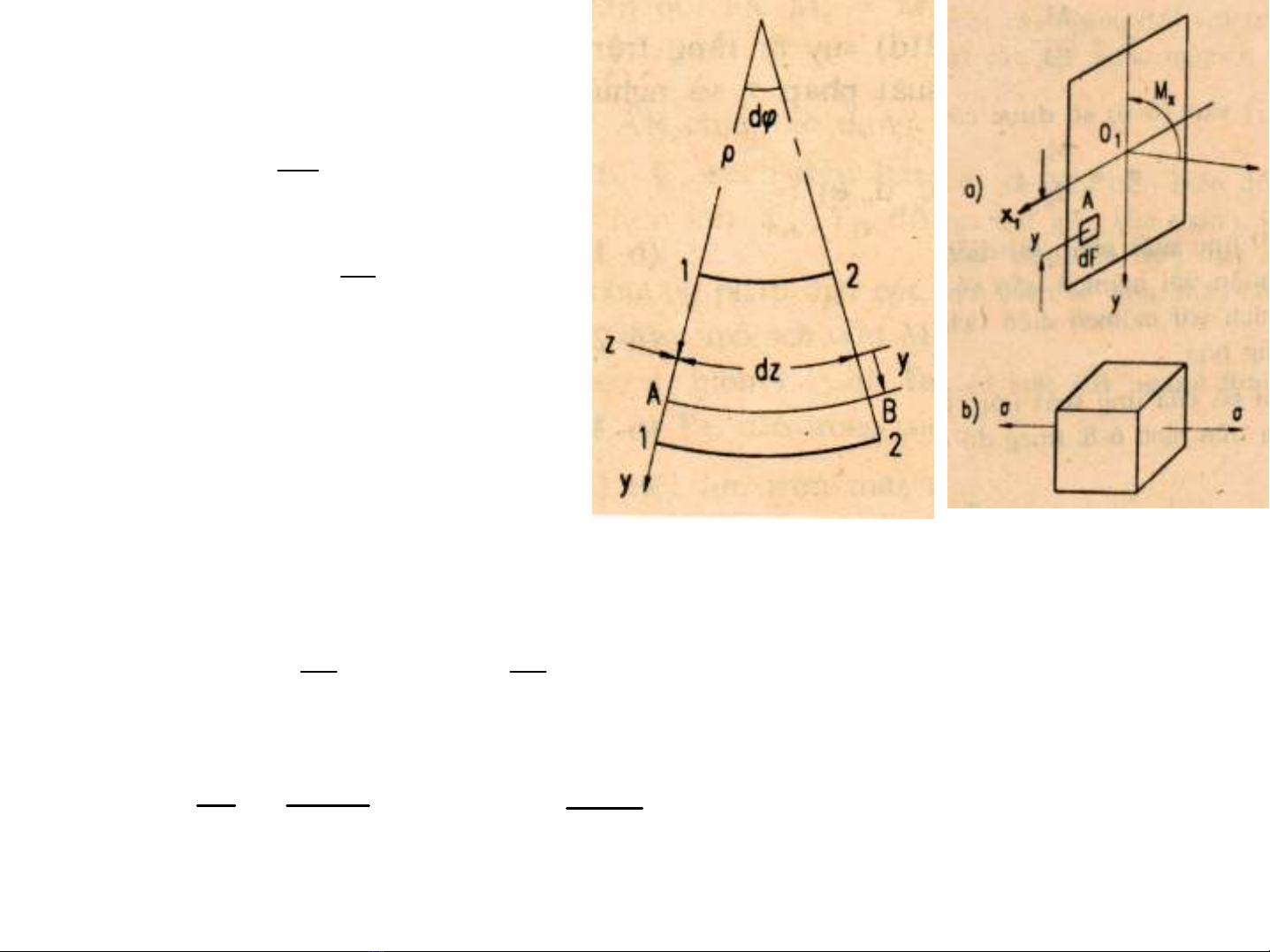
2.1.3. TÝnh øng suÊt
- §Þnh luËt Hóc
- Thay:
-Vμ
-Khi
- Trôc trung hoμ®i qua träng
t©m cña mÆt c¾t ngang. HÖ
Oxy lμhÖ trôc qu¸n tÝnh chÝnh trung t©m.
- Ta cã:
- Hay:
⇒
zz E
ε
σ
=
y
E
z
ρ
σ
=
0=== ∫∫
FF
zz ydF
E
dFN
ρ
σ
0==
∫x
F
SydF
x
F
xJ
E
dFy
E
M∫==
ρρ
2
x
x
EJ
M
=
ρ
1y
J
M
x
x
z=
σ
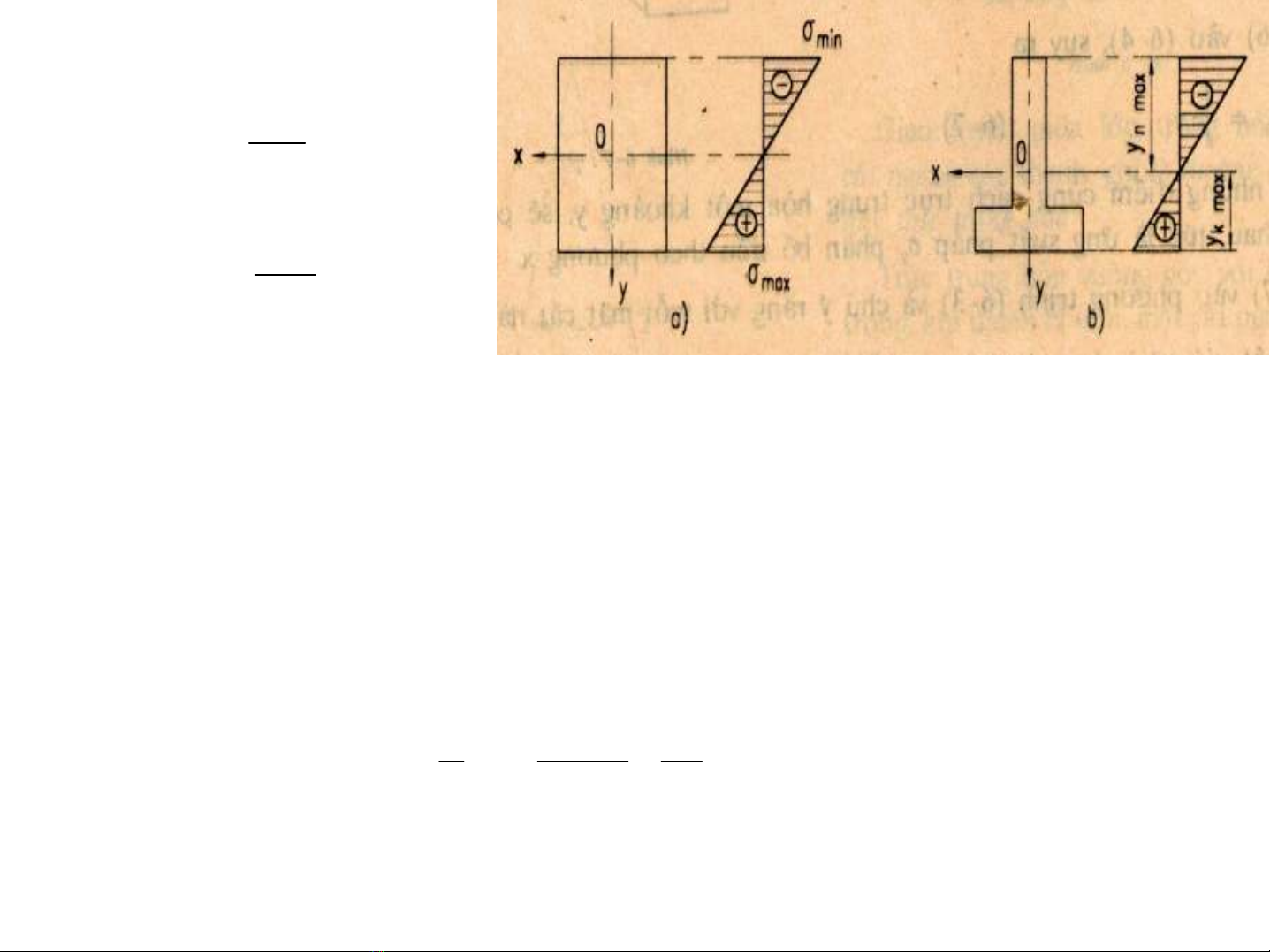
-
ø
ng suÊt lín nhÊt
- Víi ox lμtrôc ®èi xøng
σzmax = - σzmin
- M« men qu¸n tÝnh Jx cña mét sè tiÕt diÖn:
Ch÷ nhËt, vμnh kh¨n, trßn
2.2. BiÕn d¹ng
2.2.1. §é cong
-Kh¶o s¸t thanh chÞu uèn thuÇn tuý trong mÆt ph¼ng Oyz.
-§é cong cña thanh:
Trong ®ã: EJxlμ®é cøng uèn cña thanh.
2.2.2. §é vâng
-
§
−
ên
g
®μn håi ⇒®
−
ên
g
tr
ô
c - u
è
n con
g
,
®
é
vân
g
t
¹
i 1 ®i
Ó
m
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=maxmax max k
x
x
zy
J
M
σ
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=minmin min n
x
x
zy
J
M
σ
dz
d
zEJ
zM
z
x
x
ϕ
ρ
== )(
)(
)(
1


























