1
1
1
VËT Lý HIÖn ®¹i
(modern physics)
Ch
Ch−¬
−¬ng 2
ng 2
Thêi l−îng: 3 ®vht
Gi¶ng viªn: TS. TrÇn ThÞ T©m
2
CH−¬NG II: mét sè vÊn ®Ò c¬ b¶n cña
vËt lý l−îng tö
(6:2)
2.1 Gi¶ thiÕt cña De Broglie vÒ l−ìng tÝnh
sãng h¹t cña h¹t vi m«.
2.2 KiÓm chøng gi¶ thiÕt cña De Broglie: ThÝ
nghiÖm cña Davisson-Germer, thÝ nghiÖm
cña Thomson. Mét sè øng dông cña sãng
vËt chÊt.
2.3 Hµm sãng
2.4 Sãng ¸nh s¸ng vµ photon
2.1 Gi
2.1 Gi
thiÕt c
thiÕt cñ
ña De Broglie vÒ l
a De Broglie vÒ l−ì
−ìng tÝnh
ng tÝnh
sãng h
sãng h¹
¹t c
t cñ
ña h
a h¹
¹t vi m
t vi m«
«.
.
2.2 Ki
2.2 KiÓ
Óm ch
m chø
øng gi
ng gi
thiÕt c
thiÕt cñ
ña De Broglie: ThÝ
a De Broglie: ThÝ
nghi
nghiÖ
Öm c
m cñ
ña Davisson
a Davisson-
-Germer, thÝ nghi
Germer, thÝ nghiÖ
Öm
m
c
cñ
ña Thomson. M
a Thomson. Mé
ét s
t sè
èø
øng dông c
ng dông cñ
ña sãng
a sãng
v
vË
Ët
t chÊt.
chÊt.
2.3
2.3 H
Hµ
µm sãng
m sãng
2.4
2.4 Sãng
Sãng ¸
¸nh s
nh s¸
¸ng v
ng vµ
µphoton
photon
3
CH−¬NG II: mét sè vÊn ®Ò c¬ b¶n cña
vËt lý l−îng tö
(tiÕp theo)
2.5 Sãng vËt chÊt vµ ®iÖn tö. N¨ng l−îng cña
c¸c tr¹ng th¸i cho phÐp. N¨ng l−îng ®iÓm
zero.
2.6 Nguyªn tö Hydro.
2.7 HiÖu øng ®−êng ngÇm
2.8 Nguyªn lý bÊt ®Þnh Heizenberg
2.9 Sãng vµ h¹t
2.5 Sãng vËt chÊt vµ ®iÖn tö. N¨ng l−îng cña
c¸c tr¹ng th¸i cho phÐp. N¨ng l−îng ®iÓm
zero.
2.6 Nguyªn tö Hydro.
2.7 HiÖu øng ®−êng ngÇm
2.8 Nguyªn lý bÊt ®Þnh Heizenberg
2.9 Sãng vµ h¹t
4
2.1 Gi¶ thiÕt cña De Broglie vÒ l−ìng tÝnh
sãng - h¹t cña h¹t vi m«.
Sãng vËt chÊt?
Ng−êi ta cã thÓ ®Æt ra c©u hái:
LiÖu khi
¸nh s¸ng ho¹t ®éng nh−mét h¹t, vËy c¸c
h¹t vËt chÊt cã thÓ ho¹t ®éng nh−lµ mét
sãng kh«ng?
C©u tr¶ lêi lµ: Cã
Lêi gi¶i n»m trong lÜnh vùc nghiªn cøu cña c¬ l−îng tö, lµ
®èi t−îng vµ môc ®Ých nghiªn cøu cña m«n häc nµy.
C©u tr¶ lêi lµ: Cã
Cã
Lêi gi¶i n»m trong lÜnh vùc nghiªn cøu cña c¬ l−îng tö, lµ
®èi t−îng vµ môc ®Ých nghiªn cøu cña m«n häc nµy.
2
2
5
Ta hiÓu thÕ nµo vÒ l−ìng tÝnh sãng - h¹t
cña bøc x¹ ®iÖn tõ?
Quan ®iÓm sãng
Giao thoa
NhiÔu x¹
Ph©n cùc
Sãng -
ν
,
λ
Quan ®iÓm h¹t
HiÖu øng quang ®iÖn
HiÖu øng Compton
Tia X
h¹t - E, p
6
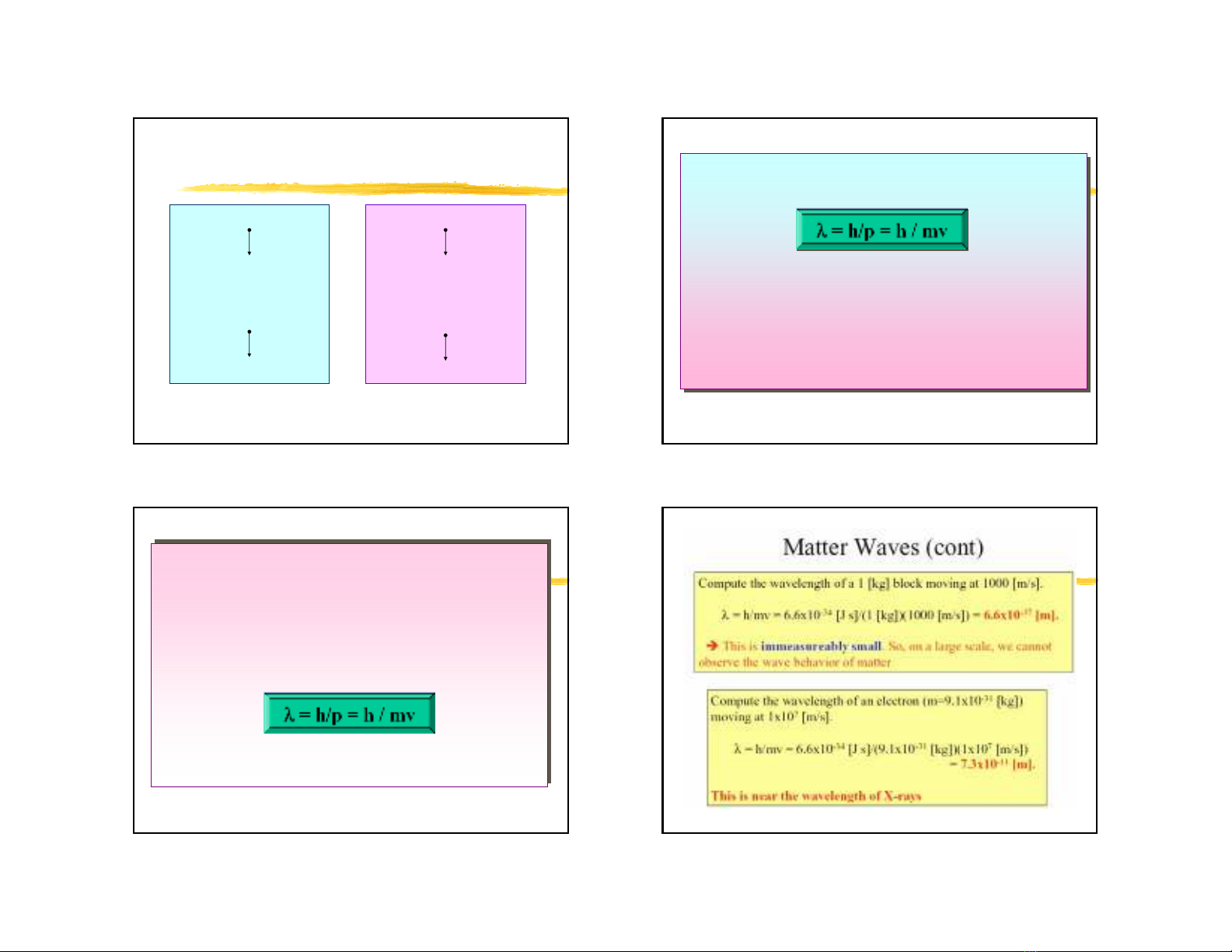
C¸c h¹t còng cã b−íc sãng theo biÓu thøc sau:
Nh−vËy, b−íc sãng cña h¹t phô thuéc vµo
moment cña chÝnh nã, gièng hÖt nh−photon.
Sù kh¸c nhau chÝnh ®ã lµ c¸c h¹t vËt chÊt cã
khèi l−îng, cßn photon th× kh«ng cã.
C¸c h¹t còng cã b−íc sãng theo biÓu thøc sau:
Nh−vËy, b−íc sãng cña h¹t phô thuéc vµo
moment cña chÝnh nã, gièng hÖt nh−photon.
Sù kh¸c nhau chÝnh ®ã lµ c¸c h¹t vËt chÊt cã
khèi l−îng, cßn photon th× kh«ng cã.
7
Nãi mét c¸ch tæng qu¸t h¬n, chuyÓn ®éng cña ®iÖn tö
còng nh−cña tÊt c¶ c¸c h¹t vi m« ®Òu lµ qu¸ tr×nh truyÒn
sãng – mét lo¹i sãng míi tr−íc ®©y ch−a hÒ ®−îc biÕt
®Õn, gäi lµ
sãng de Broglie
. §©y lµ hÖ thøc (theo
de Broglie) cã thÓ dïng ®Ó g¸n b−íc sãng cho h¹t vËt
chÊt cã xung l−îng cho tr−íc. B−íc sãng ®−îc tÝnh tõ
c«ng thøc trªn ®−îc gäi lµ b−íc sãng de Broglie.
chó ý tíi vai trß trung t©m cña h»ng sè Planck
h
trong viÖc nèi kÕt
c¸c ph−¬ng diÖn sãng vµ h¹t cña c¶ ¸nh s¸ng lÉn vËt chÊt!!!.
Nãi mét c¸ch tæng qu¸t h¬n, chuyÓn ®éng cña ®iÖn tö
còng nh−cña tÊt c¶ c¸c h¹t vi m« ®Òu lµ qu¸ tr×nh truyÒn
sãng – mét lo¹i sãng míi tr−íc ®©y ch−a hÒ ®−îc biÕt
®Õn, gäi lµ
sãng de Broglie
. §©y lµ hÖ thøc (theo
de Broglie) cã thÓ dïng ®Ó g¸n b−íc sãng cho h¹t vËt
chÊt cã xung l−îng cho tr−íc. B−íc sãng ®−îc tÝnh tõ
c«ng thøc trªn ®−îc gäi lµ b−íc sãng de Broglie.
chó ý tíi vai trß trung t©m cña h»ng sè Planck
h
trong viÖc nèi kÕt
c¸c ph−¬ng diÖn sãng vµ h¹t cña c¶ ¸nh s¸ng lÉn vËt chÊt!!!.
8
3
3
910
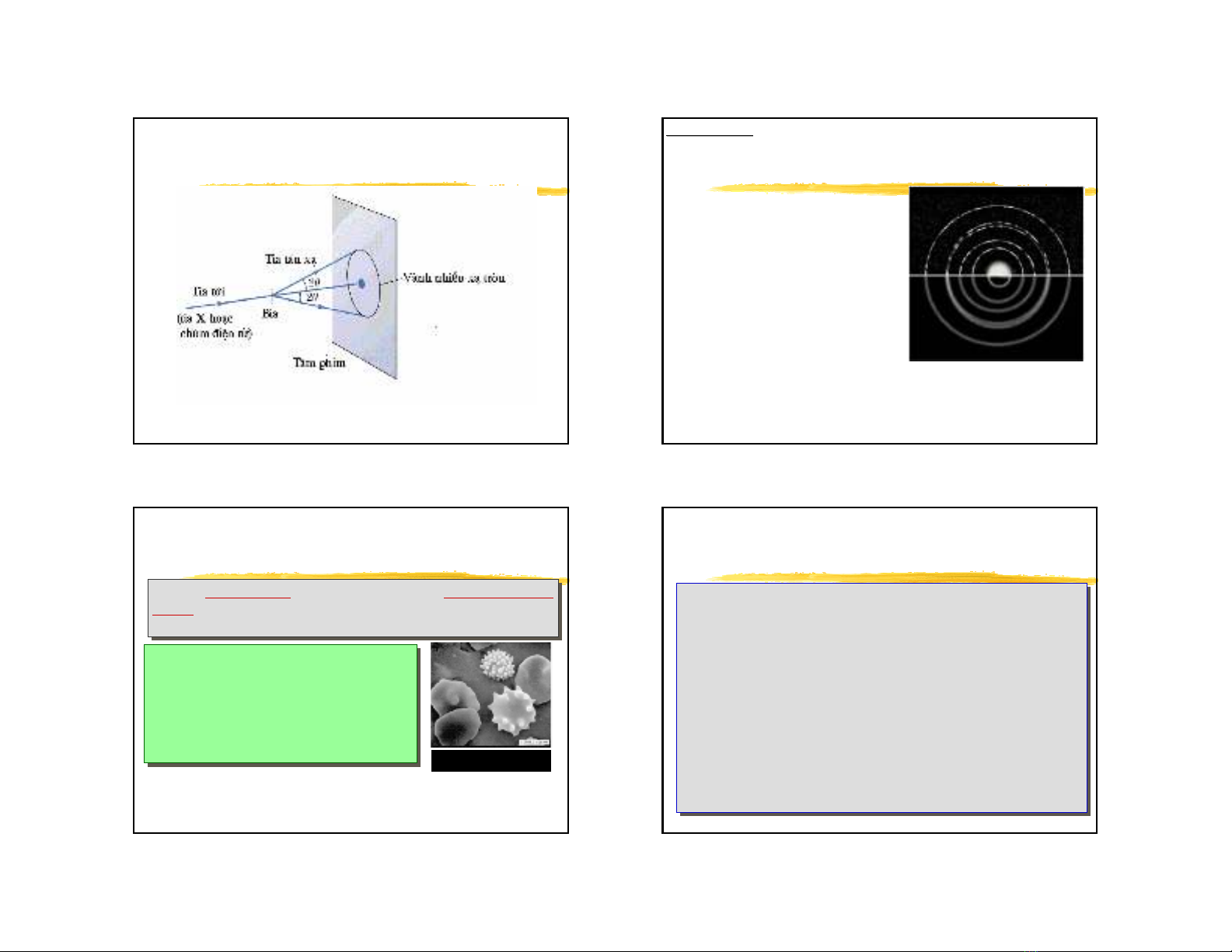
Nh÷ng hiÖu qu¶ l«gic cña gi¶ thiÕt vÒ sãng de
Broglie: Sù nhiÔu x¹ cña c¸c h¹t
Li
LiÖ
Öu c
u c¸
¸c h
c h¹
¹t v
t vË
Ët chÊt cã th
t chÊt cã thÓ
Óhi
hiÖ
Ön tÝnh chÊt sãng (vÝ dô nh
n tÝnh chÊt sãng (vÝ dô nh−
−nhiÔu
nhiÔu
x
x¹
¹) gi
) giè
èng nh
ng nh−
−tia X ho
tia X hoÆ
Æc
c ¸
¸nh s
nh s¸
¸ng v
ng vï
ïng nh
ng nh×
×n thÊy?
n thÊy?
•NÕu chóng nhiÔu x¹ th× de Broglie ®· gi¶ thiÕt ®óng, vµ c¸c h¹t
vËt chÊt cã sãng liªn ®íi m« t¶ chuyÓn ®éng cña chóng (gièng nh−
c¸c bøc x¹ ®iÖn tõ- tr−êng ®iÖn tõ)
Ta xem xÐt 1 ®iÖn tö, vµ tÝnh b−íc sãng de Broglie cña nã, khi
®iÖn tö ®−îc gia tèc b»ng hiÖu ®iÖn thÕ V.
•NÕu nh−V= 150 V th×
λ
= 1Åvµ nh÷ng ®iÖn tö nµy cã b−íc
sãng cïng bËc víi b−íc sãng tia X, nªn chóng ta cã thÓ quan s¸t
hiÖu øng nhiÔu x¹ b»ng c¸ch sö dông m¹ng tinh thÓ nh−c¸ch tö
nhiÔu x¹ (gièng nh−®èi víi tia X) vµ nÕu ta quan s¸t thÊy hiÖn
t−îng nhiÔu x¹ ⇒de Broglie ®· gi¶ thiÕt ®óng!
•NÕu nh−V= 150 V th×
λ
= 1Åvµ nh÷ng ®iÖn tö nµy cã b−íc
sãng cïng bËc víi b−íc sãng tia X, nªn chóng ta cã thÓ quan s¸t
hiÖu øng nhiÔu x¹ b»ng c¸ch sö dông m¹ng tinh thÓ nh−c¸ch tö
nhiÔu x¹ (gièng nh−®èi víi tia X) vµ nÕu ta quan s¸t thÊy hiÖn
t−îng nhiÔu x¹ ⇒de Broglie ®· gi¶ thiÕt ®óng!
11
2.2
2.2 Ki
KiÓ
Óm ch
m chø
øng gi
ng gi
thiÕt c
thiÕt cñ
ña De Broglie:
a De Broglie:
ThÝ
ThÝ nghi
nghiÖ
Öm c
m cñ
ña Davisson
a Davisson-
-Germer, thÝ
Germer, thÝ
nghi
nghiÖ
Öm c
m cñ
ña Thomson. M
a Thomson. Mé
ét s
t sè
èø
øng dông
ng dông
c
cñ
ña sãng v
a sãng vË
Ët chÊt.
t chÊt.
ThÝ nghiÖm Davisson - Germer
12
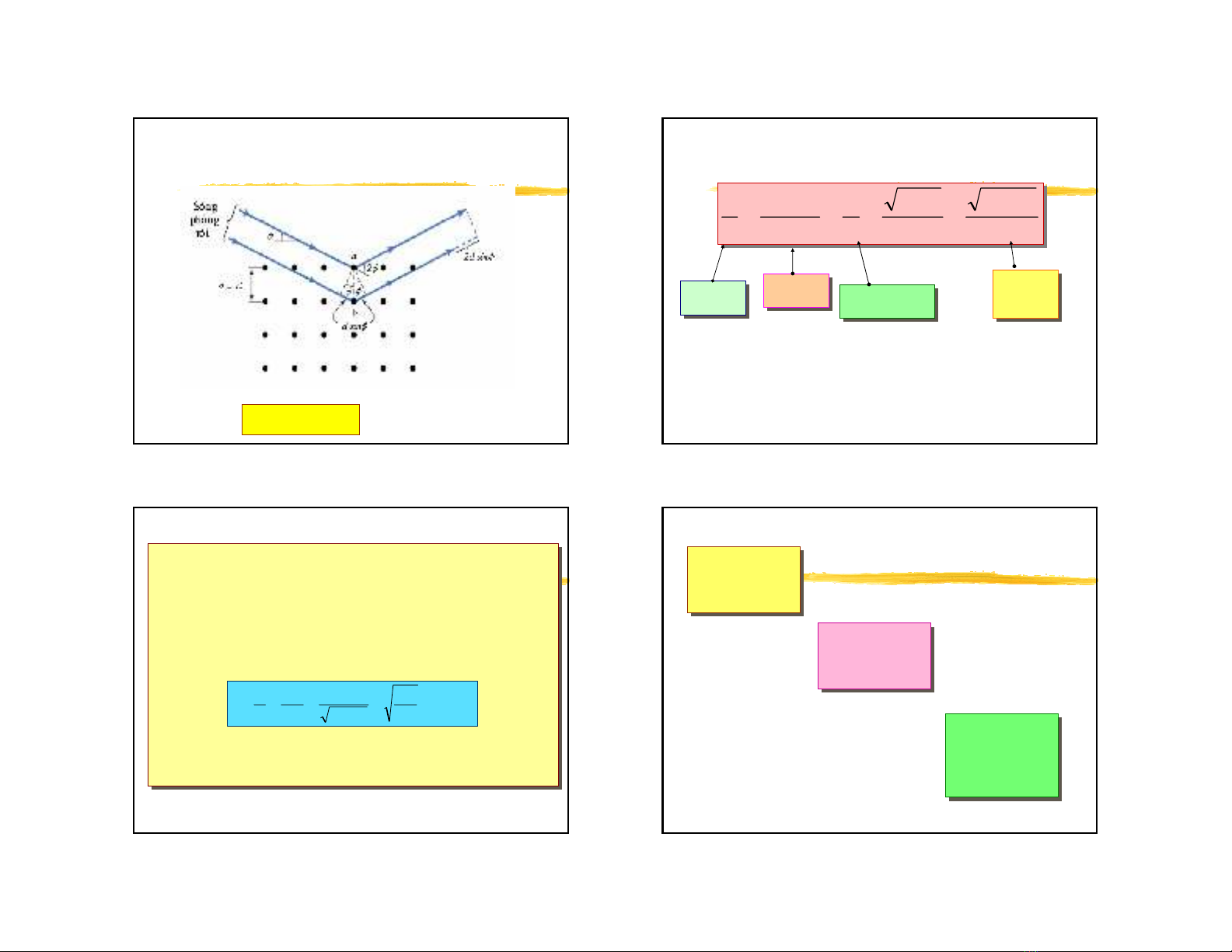
§å thÞ theo täa ®é cùc cña c−êng ®é dßng víi c¸c thÕ gia tèc
kh¸c nhau. Chïm nhiÔu x¹ m¹nh râ rÖt ë gãc
φ
= 500 ®èi víi
V=54V . NÕu ®iÖn thÕ gia tèc h¬i t¨ng hoÆc gi¶m th× c−êng ®é
tia nhiÔu x¹ ®Òu gi¶m.
4
4
13
H×nh ¶nh s¬ l−îc vÒ c¸c nguyªn tö t¹o nªn m¹ng tinh thÓ trong thÝ
nghiÖm. Tinh thÓ xö sù nh−mét c¸ch tö nhiÔu x¹, c¸c ®−êng
nguyªn tö c¸ch nhau mét kho¶ng là d. §èi víi tinh thÓ niken ®−îc
dïng trong thÝ nghiÖm trªn th× d= 215 pm
Cùc ®¹i chÝnh ®èi víi c¸ch tö nµy ph¶i tháa m·n ®iÒu kiÖn Bragg:
m= 1, 2, 3, ...
λ
φ
md =sin 14
h
meV
h
mE
h
p
d
m22
sin
1====
θ
λ
B−íc sãng
cña ®iÖn tö
B−íc sãng
cña ®iÖn tö
§iÒu kiÖn
Bragg
§iÒu kiÖn
Bragg Mèi t−¬ng quan
de Broglie
Mèi t−¬ng quan
de Broglie
Gia tèc qua
hiÖu ®iÖn
thÕ V
Gia tèc qua
hiÖu ®iÖn
thÕ V
15
§ã cã ph¶i lµ cùc ®¹i nhiÔu x¹?:
•Do d= 215 pm ®èi víi Ni, vµ
φ
= 500 vµ m= 1, ®iÒu kiÖn ®Ó t¹o
nªn giao thoa
λ
= d sin
φ
= 215 sin 500 [pm] = 165 pm
•B−íc sãng de Broglie tÝnh theo thÕ gia tèc:
B−íc sãng cña ®iÖn tö
hoµn toµn
phï hîp rÊt tèt víi
cùc ®¹i phæ nhiÔu x¹ !!!
§ã cã ph¶i lµ cùc ®¹i nhiÔu x¹?:
•Do d= 215 pm ®èi víi Ni, vµ
φ
= 500 vµ m= 1, ®iÒu kiÖn ®Ó t¹o
nªn giao thoa
λ
= d sin
φ
= 215 sin 500 [pm] = 165 pm
•B−íc sãng de Broglie tÝnh theo thÕ gia tèc:
B−íc sãng cña ®iÖn tö
hoµn toµn
phï hîp rÊt tèt víi
cùc ®¹i phæ nhiÔu x¹ !!!
pm
V
meV
h
m
h
p
h167
150
2=====
υ
λ
16
1924
Gi¶ thiÕt
deBroglie ra ®êi
1924
1924
Gi¶ thiÕt
deBroglie ra ®êi
1927
ThÝ nghiÖm
Davisson-Germer
1927
1927
ThÝ nghiÖm
Davisson-Germer
1929
Gi¶i th−ëng
Nobel cho
deBroglie
1929
1929
Gi¶i th−ëng
Nobel cho
deBroglie
5
5
17
ThÝ nghiÖm cña G.P. Thomson (1927)
18
G. P. Thomson
G. P. Thomson
• Lµ con trai cña J. J. Thomson - ng−êi
®· x¸c ®Þnh ®iÖn tö lµ mét h¹t, cã nghÜa
lµ cã khèi l−îng, moment vµ n¨ng
l−îng - ®−îc gi¶i Nobel n¨m 1906.
• G. P. Thomson chøng minh ®−îc tÝnh
chÊt sãng cña ®iÖn tö - ®ång h−ëng gi¶i
Nobel víi Davisson n¨m 1937.
• ¤ng chiÕu mét chïm tia ®iÖn tö ®¬n
n¨ng qua mét tÊm kim lo¹i máng ∼
1µm (Ke ∼10-60 keV) vµ quan s¸t thÊy
c¸c vµnh trßn nhiÔu x¹ ®ång t©m nh−
tr−íc kia ®· quan s¸t ®−îc víi tia X.
•HÖ thÝ nghiÖm vµ kÕt qu¶ - vÒ c¬ b¶n dùa trªn thÝ nghiÖm nhiÔu x¹ cña
Debye-Sherrer trªn tÊm kim lo¹i máng nh−ng dïng chïm tia ®iÖn tö thay
chç tia X.
19
Mét sè øng dông cña sãng vËt chÊt
KÝnh hiÓn vi ®iÖn tö
⇒KÝnh hiÓn vi ®iÖn tö lµ mét thiÕt bÞ øng dông tÝnh chÊt sãng cña
®iÖn tö ®Ó nh×n thÊy nh÷ng h×nh ¶nh mµ kh«ng thÓ thÊy ®−îc b»ng
kÝnh hiÓn vi quang häc b×nh th−êng !!!
⇒KÝnh hiÓn vi ®iÖn tö lµ mét thiÕt bÞ øng dông tÝnh chÊt sãng cña
®iÖn tö ®Ó nh×n thÊy nh÷ng h×nh ¶nh mµ kh«ng thÓ thÊy ®−îc b»ng
kÝnh hiÓn vi quang häc b×nh th−êng !!!
TÕ bµo m¸u
H×nh ¶nh nµy thu ®−îc khi dïng kÝnh hiÓn vi
®iÖn tö quÐt SEM (Scanning Electron
Microscope).
ThiÕt bÞ nµy cã ®é ph©n gi¶i xuèng tíi xÊp xØ
1 nm - mét 100 lÇn cao h¬n kÝnh hiÓn vi
quang häc dïng ¸nh s¸ng vïng nh×n thÊy.
H×nh ¶nh nµy thu ®−îc khi dïng kÝnh hiÓn vi
®iÖn tö quÐt SEM
SEM (Scanning Electron
Microscope).
ThiÕt bÞ nµy cã ®é ph©n gi¶i xuèng tíi xÊp xØ
1 nm - mét 100 lÇn cao h¬n kÝnh hiÓn vi
quang häc dïng ¸nh s¸ng vïng nh×n thÊy.
§iÓm quan träng ë ®©y: C¸c h¹t cã n¨ng l−îng cao ®−îc
dïng ®Ó ph¸t hiÖn cÊu tróc cña vËt chÊt 20
Vµi Lêi b×nh luËn vÒ ®Çu dß b»ng
h¹t vËt chÊt
⌧Chóng ta võa kh¼ng ®Þnh r»ng c¸c h¹t cã n¨ng l−îng
cao (®iÖn tö trong tr−êng hîp SEM) cã thÓ dïng ®Ó ph¸t
hiÖn cÊu tróc cña vËt chÊt khi kÝnh hiÓn vi quang häc b×nh
th−êng kh«ng thÓ. C¸c sãng vËt chÊt lµ mét bæ sung rÊt cã
gi¸ trÞ cho tia X trong viÖc nghiªn cøu cÊu tróc nguyªn tö
cña chÊt r¾n.
⌧Moment cña h¹t cµng cao, th× b−íc sãng de Broglie
cµng nhá.
⌧Khi b−íc sãng cµng nhá, cµng cã thÓ ph¸t hiÖn tinh tÕ
h¬n cÊu tróc cña vËt chÊt.
⌧Chóng ta võa kh¼ng ®Þnh r»ng c
c¸
¸c h
c h¹
¹t cã n
t cã n¨
¨ng l
ng l−î
−îng
ng
cao
cao (®iÖn tö trong tr−êng hîp SEM) cã thÓ dïng ®Ó ph
ph¸
¸t
t
hi
hiÖ
Ön cÊu tr
n cÊu tró
óc c
c cñ
ña v
a vË
Ët chÊt
t chÊt khi kÝnh hiÓn vi quang häc b×nh
th−êng kh«ng thÓ. C¸c sãng vËt chÊt lµ mét bæ sung rÊt cã
gi¸ trÞ cho tia X trong viÖc nghiªn cøu cÊu tróc nguyªn tö
cña chÊt r¾n.
⌧Moment c
Moment cñ
ña h
a h¹
¹t c
t cµ
µng cao
ng cao, th× b−íc sãng de Broglie
cµng nhá.
⌧Khi b
b−í
−íc sãng c
c sãng cµ
µng nh
ng nhá
á, c
, cµ
µng cã th
ng cã thÓ
Óph
ph¸
¸t hi
t hiÖ
Ön tinh tÕ
n tinh tÕ
h
h¬
¬n cÊu tr
n cÊu tró
óc c
c cñ
ña v
a vË
Ët chÊt
t chÊt.