BÀI TẬP ĐIỆN XOAY CHIỀU HAY VÀ KHÓ
TRONG MÙA THI THỬ 2013
Diễn đàn www.vatliphothong.vn
Version 1 :15 Exercises
Cần Thơ,ngày 28 tháng 04 năm 2013
Câu 1: Đặt một điện áp u=U0cos ωt(V)vào hai đầu đoạn mạch gồm cuộn dây nối tiếp với một tụ
điện Ccó điện dung thay đổi được. Ban đầu tụ điện có dung kháng 100Ω , cuộn dây có cảm kháng
50Ω . Giảm điện dung một lượng ∆C= 10−3/(8π)(F).thì tần số góc dao động riêng của mạch là
80πrad/s . Tần số góc ωcủa dòng điện trong mạch là:
A. 50πrad/s.
B. 100πrad/s.
C. 40πrad/s.
D. 60πrad/s.
Lời giải
Ta có C=1
100.ω (F)
⇒C1=1
100.ω −10−3
8π
L=50
ω
80π=ω0=1
√L.C1
Thay Lvà C1vào ta tính được ω= 40π
Chọn C
Câu 2: Đoạn mạch RLC mắc nối tiếp .Hiệu điện thế hai đầu đoạn mạch là u=
120√2 cos ωt(V).Khi ω=ω1= 100πrad/s thì dòng điện sớm pha hơn hiệu điện thế hai đầu
đoạn mạch góc π/6và có giá trị 1(A).Khi Khi ω=ω1= 100πrad/s và Khi ω=ω2= 400πrad/s
thì dòng điện có cùng giá trị hiệu dụng. Giá trị của Llà :
A. 0,2
π(H).B. 0,3
π(H).
C. 0,4
π(H).D. 0,5
π(H).
Lời giải
Ta có khi ω1= 100πthì inhanh pha hơn umột góc π
6nên ta có:
ZC−ZL
R=1
√3(1)
-Ta có Z=U
I= 120Ω(2)
-Từ (1) và (2) ta có
ZC−ZL= 60Ω ⇒ω1L−1
ω1C= 60(3)
-Khi ω2= 400πthì Ikhông đổi nên ta có
ZL−ZC= 60Ω ⇒ω2L−2
ω2C= 60(4)
1
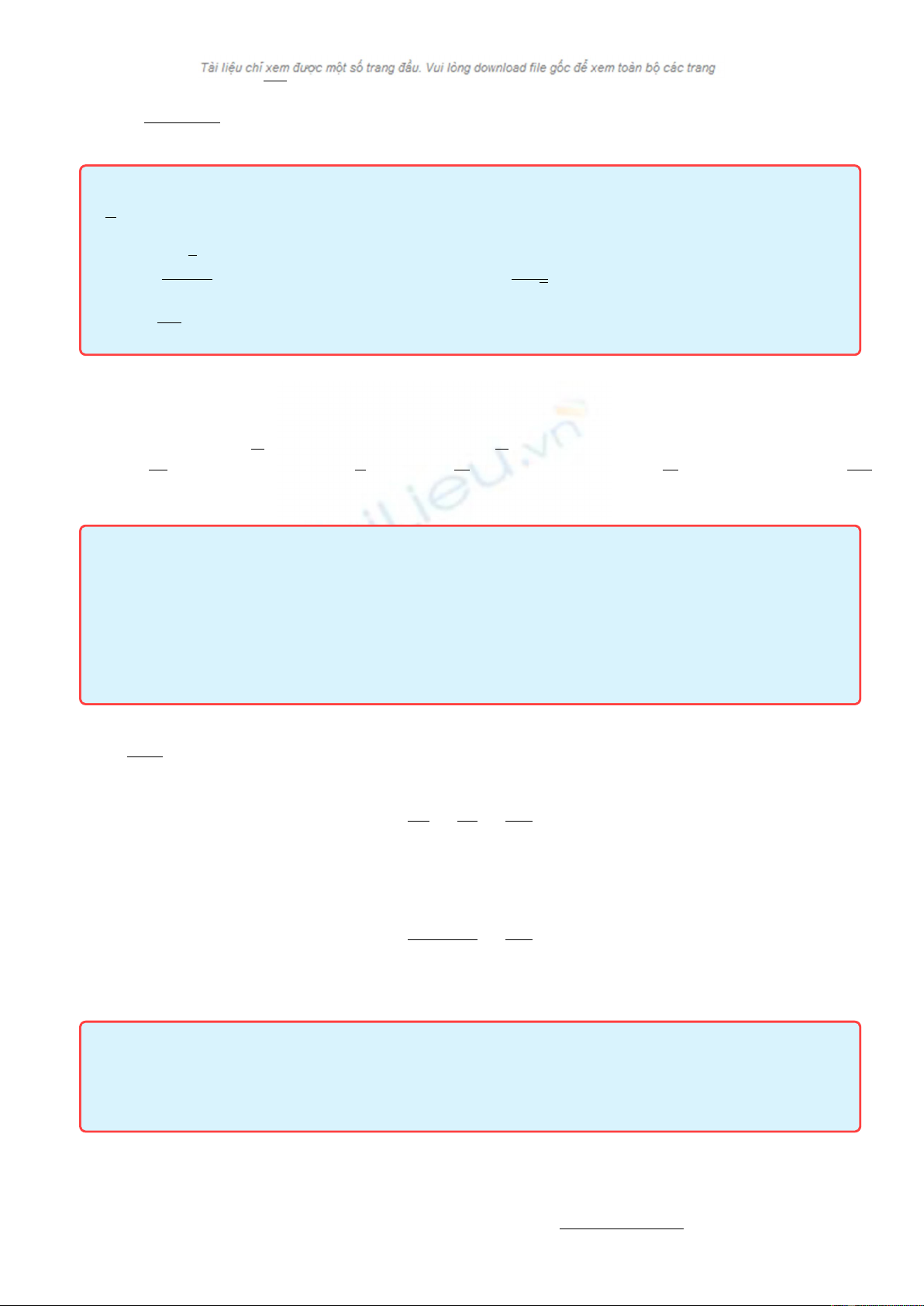
-Từ (3) và (4) ta có L=0.2
π
Và C=1,25.10−4
π
Đáp án : A
Câu 3: Dòng điện xoay chiều hình sin chạy qua mạch có biểu thức cường độ là i=I0cos(ωt −
π
2)(A),I0>0.Tính từ lúc t= 0(s)điện lượng chuyển qua tiết diện thẳng dây dẫn của đoạn mạch
đó trong thời gian một nửa chu kỳ dòng điện là :
A. π√2I0
ω.B. πI0
ω√2.
C. 2I0
ω.D. 0.
Lời giải
Lượng điên tích dịch chuyển qua dây sẽ được tính theo công thức
i=q0=dq
dt ⇒q=Z
T
2
0
I0cos(ωt−π
2)dt ⇔q=I0
ωZ
T
2
0
sin(ωt)dt ⇔q=−I0
ω(cos π−cos 0) ⇔q=2I0
ω
Đáp án :C
Câu 4: Một người định quấn một máy hạ áp từ điện áp U1= 220(V)xuống U2= 110(V)với lõi
không phân nhánh, xem máy biến áp là lí tưởng, khi máy làm việc thì suất điện động hiệu dụng
xuất hiện trên mỗi vòng dây là 1,25V n/vng. Người đó quấn đúng hoàn toàn cuộn thứ cấp nhưng lại
quấn ngược chiều những vòng cuối của cuộn sơ cấp. Khi thử máy với điện áp U1= 220Vthì điện
áp hai đầu cuộn thứ cấp đo được là 121(V). Số vòng dây bị quấn ngược là:
A. 9. B. 8.
C. 12. D. 10.
Lời giải
N1=220
1,25 = 176 vòng
Nếu không quấn ngược thì ta có
N2
N1
=U2
U1
=110
220
⇒N2= 88
Gọi số vòng quấn ngược là x, khi đó ta có thể hiểu như số vòng được quấn ở cuộn sơ cấp chỉ là 176 −2x
Khi đó 176 −2x
88 =220
121
⇒x= 8
Chọn B
Câu 5: Đặt điện áp 200V−50Hz vào đoạn mạch R(Lr)C,trong đó r= 40Ω,ZL= 60Ω,ZC= 80Ω
và biến trở Rthuộc 0≤R < ∞.Khi thay đổi Rthì công suất của mạch cực đại bằng :
A. 1000W.B. 144W.
C. 800W.D. 125W.
Lời giải
Ta đã có công thức giải nhanh là Pmax ⇔R=|ZL−ZC| − r
Mà
r= 40 >|ZL−ZC|= 20Pmax ⇔R= 0Pmax =U2r
r2+|ZL−ZC|2= 800W
2
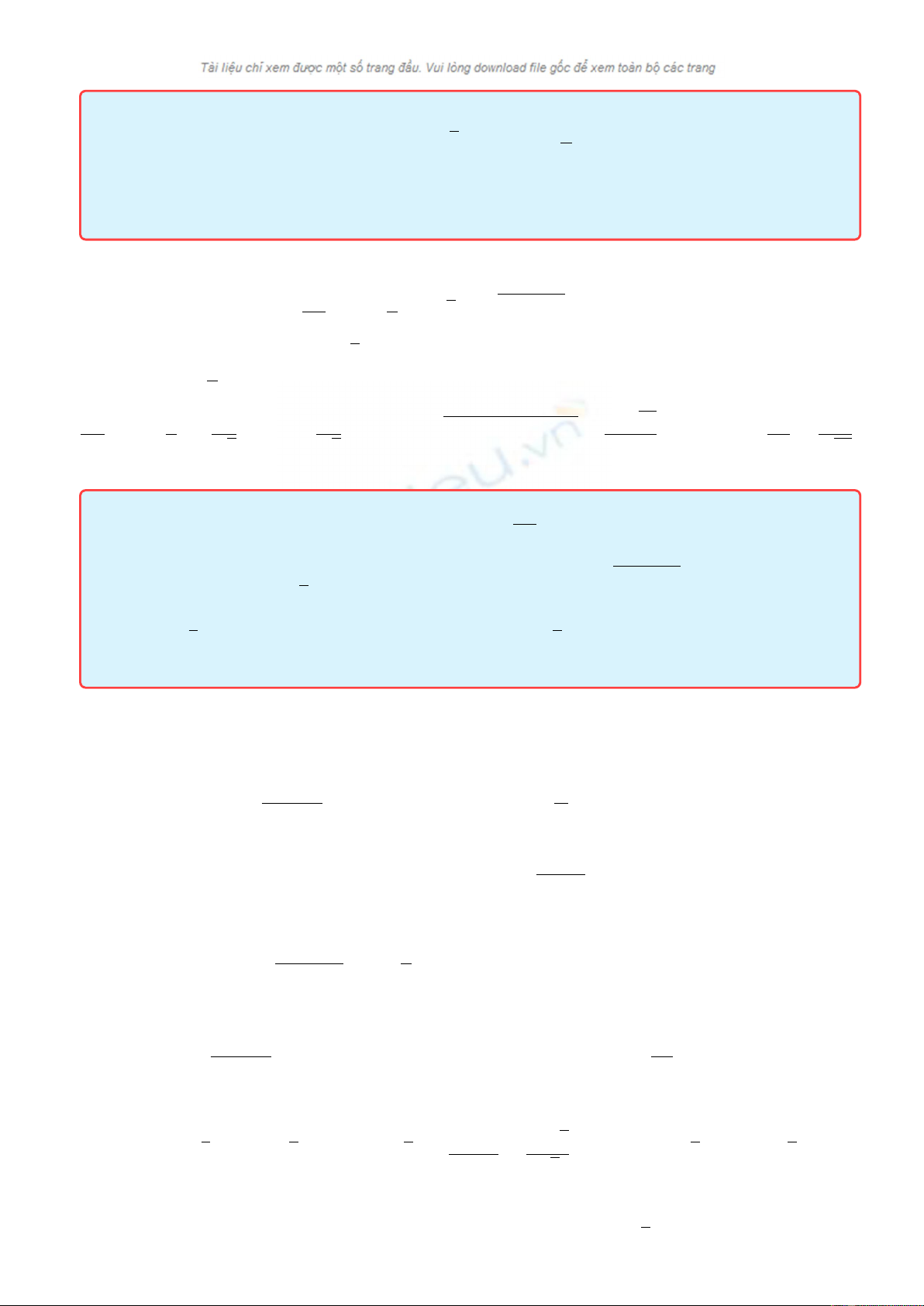
Đáp án : C
Câu 6: Cho mạch điện LRC mắc nối tiếp (Cuộn dây thuần).Biểu thức cường độ dòng điện qua
mạch là i=i0cos 100πt(A).Biết uLR = 100√2 cos(100πt +π
3)(V)và lệch pha π/2so với điện áp
của đoạn mạch RC.Hệ số công suất của đoạn mạch là :
A. 0,845 .B. 0,534.
C. 0,654.D. 0,926.
Lời giải
Ta có UL
UR
= tan(π
3) = √3(1)qU2
R+U2
L= 100(2)
Từ (1),(2) ⇒UR= 50V;UL= 50√3V
Vì ULR lệch pha π
2so với URC nên ta sẽ có
UC
UR
= tan(π
6) = 1
√3⇒UC=50
√3V⇔U=qU2
R+ (UL−UC)2=50√21
3V⇒cos α=UR
U=3
√21 ≈0,654
Đáp án :C
Câu 7: Mạch điện xoay chiều gồm cuộn dây có L=0.4
π(H)mắc nối tiếp với tụ điện C.Đặt vào
hai đầu đoạn mạch một điện áp u=U0cos(ωt)(V).Khi C=C1=2,5.10−3
π(F)thì hiệu điện thế
hai đầu tụ UCmax = 100√5(V).Khi C= 2,5C1thì cường độ dòng điện trễ pha π/4so với điện áp
hai đầu đoạn mạch.Giá trị của U0là :
A. 50√2(V).B. 100√2(V).
C. 200(V).D. 150(V).
Lời giải
Ta có .Khi C= 2,5C1thì cường độ dòng điện trễ pha π/4so với điện áp hai đầu đoạn mạch chứng tỏ còn
có điện trở thuồn r Khi
UCmax ⇔ZCmax =r2+Z2
L
ZL
() ⇒ZLZCmax =r2+Z2
L⇒L
C=r2+Z2
L⇒r2+Z2
L= 160Ω(1)
Khi
C= 2,5Cmax ⇔ZC=ZCmax
2,5
Cường độ dòng điện trễ pha π/4so với điện áp hai đầu đoạn mạch nên ta có Khi đó
ZL−ZC
r= tan π
4= 1 ⇒ZCmax = 2,5(ZL−r)(2)
Thế (2) vào ∗ta có
r2+Z2
L
ZL
= 2,5(ZL−r)⇒1,5Z2
L−2,5ZLr−r2= 0 ⇒ZL
r= 2(3)
Từ (1)và(3) ta có
r= 4√2; ZL= 8√2; Zmax = 10√2I=UCmax
ZCmax
=10√5
√2A⇒Ur= 40√5; UL= 80√5
Mặt khác khi UCmaxthì Uvuông pha với ULr nên
U2=U2
Cmax −U2
r−U2
L= 100 ⇒U0= 100√2
3