1
CÁC BÀI TOÁN VỀ HÌNH HỌC TỔ HỢP
Lê Phúc Lữ - Thành phố Hồ Chí Minh
I. Kiến thức cần nhớ.
1. Các khái niệm cơ bản về hình học tổ hợp.
- Khoảng cách: từ điểm
M
đến hình
()H
là
{ }
min | ( )MN N H∈
.
Chẳng hạn nếu
()H
là một điểm thì khoảng cách từ
M
đến hình
()H
chính là độ dài đoạn
thẳng, nếu
()H
là đường tròn
()O
thì đó chính là khoảng cách từ
M
đến giao điểm gần nhất
của
MO
với đường tròn,...
h
O
M
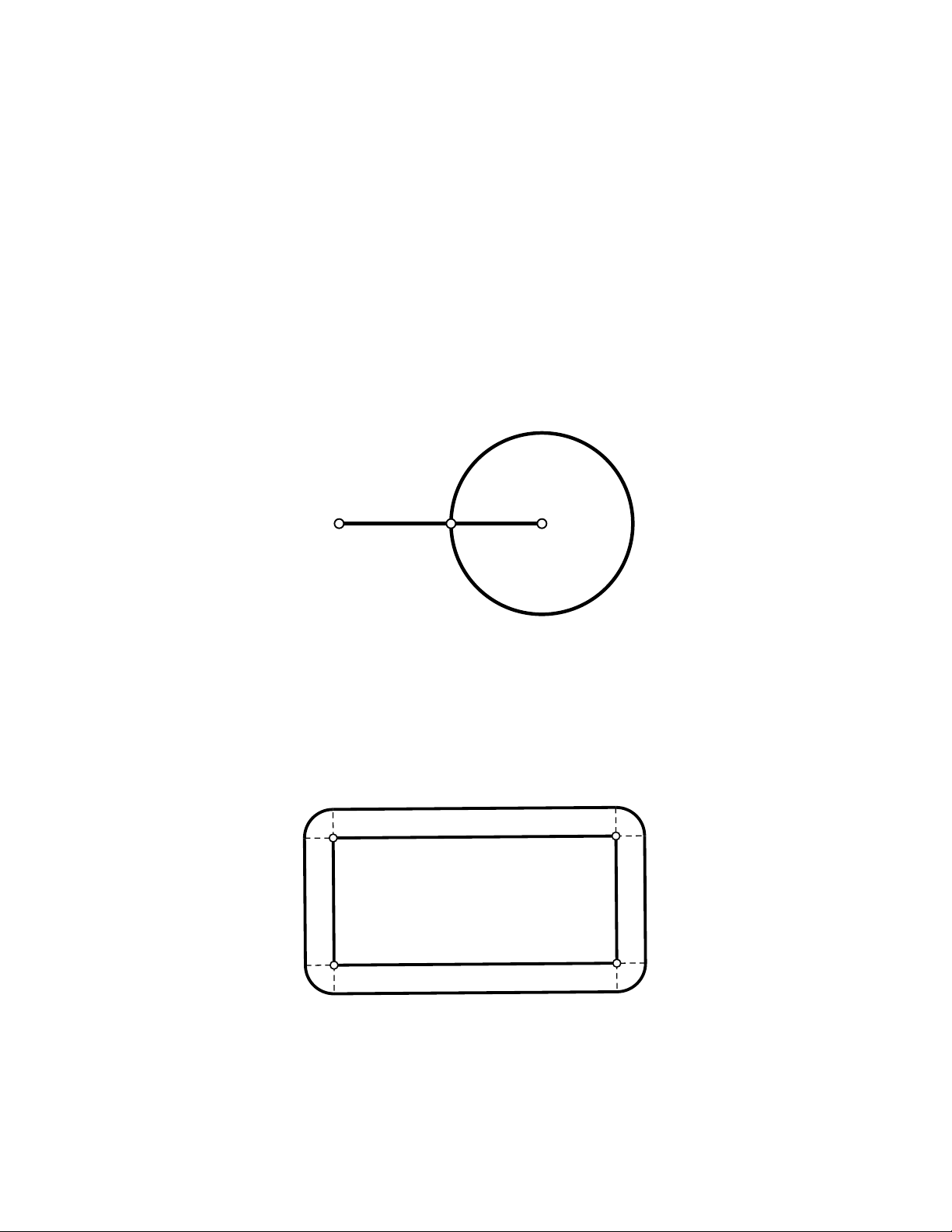
- Lân cận: bán kính
d
của hình
()H
là tập hợp các điểm
M
có khoảng cách đến
()H
không
vượt quá
d
.
Chẳng hạn: lân cận của một điểm là một hình tròn, lân cận của một đường tròn là một hình
xuyến, lân cận của một đoạn thẳng là hai hình chữ nhật và hai nửa hình tròn, lân cận của một đa
giác là gồm nhiều hình chữ nhật và nhiều phần của một hình tròn.
C
A
B
D
- Bao lồi: của một hệ điểm là đa giác lồi có đỉnh thuộc hệ điểm đã cho, có chu vi nhỏ nhất và
chứa toàn bộ hệ điểm đó. Bao lồi là một công cụ mạnh, không chỉ để giải quyết các bài toán
mang tính lý thuyết mà còn cả những bài mang tính thực tiễn cao.
2
- Điểm nguyên: trong hệ trục tọa độ vuông góc
Oxy
hoặc trong không gian
Oxyz
là những
điểm có tọa độ đều là các số nguyên.
2. Một số định lí cơ bản.
- Lân cận bán kính
d
của một đa giác có diện tích
S
, chu vi
P
có diện tích là
2
S pd d
π
++
.
- Một tam giác nội tiếp trong một hình chữ nhật thì có diện tích không vượt quá
1
2
diện tích của
hình chữ nhật đó.
- Một đa giác có khoảng cách lớn nhất giữa hai điểm
,MN
bất kì nằm trong nó không vượt quá
d
có thể nội tiếp được trong một hình tròn có đường kính là
.d
- Một đa giác có số cạnh chẵn thì tồn tại một đường chéo không song song với bất cứ cạnh nào
của đa giác.
- Định lí Pick: một đa giác lồi không tự cắt có
a
điểm nguyên trên cạnh (có tính cả đỉnh) và
b
điểm nguyên nằm phía trong thì có diện tích là
1
2
a
Sb= +−
.
II. Một số bài tập áp dụng.
Bài 1: Trong mặt phẳng cho n điểm
123
, , ,..., n
AAA A
sao cho không có ba điểm nào thẳng
hàng và không có 4 điểm nào tạo thành một hình thang. Qua mỗi điểm
, 1,
i
Ai n=
, ta vẽ các
đường thẳng song song với tất cả các đoạn thẳng
, , {1,2,3,..., }
jk
AA j kk n≠∈
. Tìm số tối đa
các giao điểm của các đường thẳng song song đã vẽ.
Giải.
Xét một điểm
,1
i
A in≤≤
nào đó, có tất cả:
2
1
( 1)( 2)
2
n
nn
C−
−−
=
đường thẳng đi qua 2 trong
1n−
điểm còn lại.
Do có tất cả n điểm nên ta có
( 1)( 2)
2
nn n−−
đường thẳng trong mặt phẳng và có
2n−
đường
thẳng cùng song song với nhau.
Ta sẽ tìm số giao điểm tối đa của một đường thẳng d đi qua điểm
,1
i
A in≤≤
nào đó với các
đường thẳng khác còn lại. Ngoài đường thẳng d ra, ta còn
( 1)( 2) 1
2
nn n
M−−
= −
đường thẳng
khác và trong đó có
( 1)( 2) 1
2
nn
N−−
= −
đường cùng đi qua
i
A
như đường thẳng d.
Do đường thẳng d song song với
3Pn= −
đường thẳng khác nên số giao điểm nhiều nhất trên
đường thẳng d là:
3
32
( 1)( 2) ( 1)( 2) 4 3 4
1 1 ( 3)
22 2
nnn nn nnn
MNP n
−− −− −++

−−= −− −−−=


.
Vì có tất cả
( 1)( 2)
2
nn n−−
đường thẳng và mỗi giao điểm như trên được tính 2 lần nên số giao
điểm tối đa có thể có là:
32
( 1)( 2)( 4 3 4)
8
nn n n n n− − − ++
.
Bài toán trên thú vị ở chỗ là nếu thay song song bởi vuông góc thì vẫn cho ra cùng một kết quả
như trên.
Bài 2. Trong mặt phẳng cho n điểm phân biệt
12
, ,..., n
AA A
sao cho không có ba điểm nào
thẳng hàng và bốn điểm nào tạo thành hình bình hành. Gọi
, 1,
i
Mi m=
là trung điểm của các
đoạn thẳng
,
ij
AA i j≠
nào đó. Gọi N là tổng độ dài các đoạn
,
ij
AA i j≠
và M là tổng độ dài
các đoạn
,
ij
MM i j≠
. Chứng minh rằng:
231
2
nn
MN
−+
<
.
Giải.
Trước hết, ta thấy rằng:
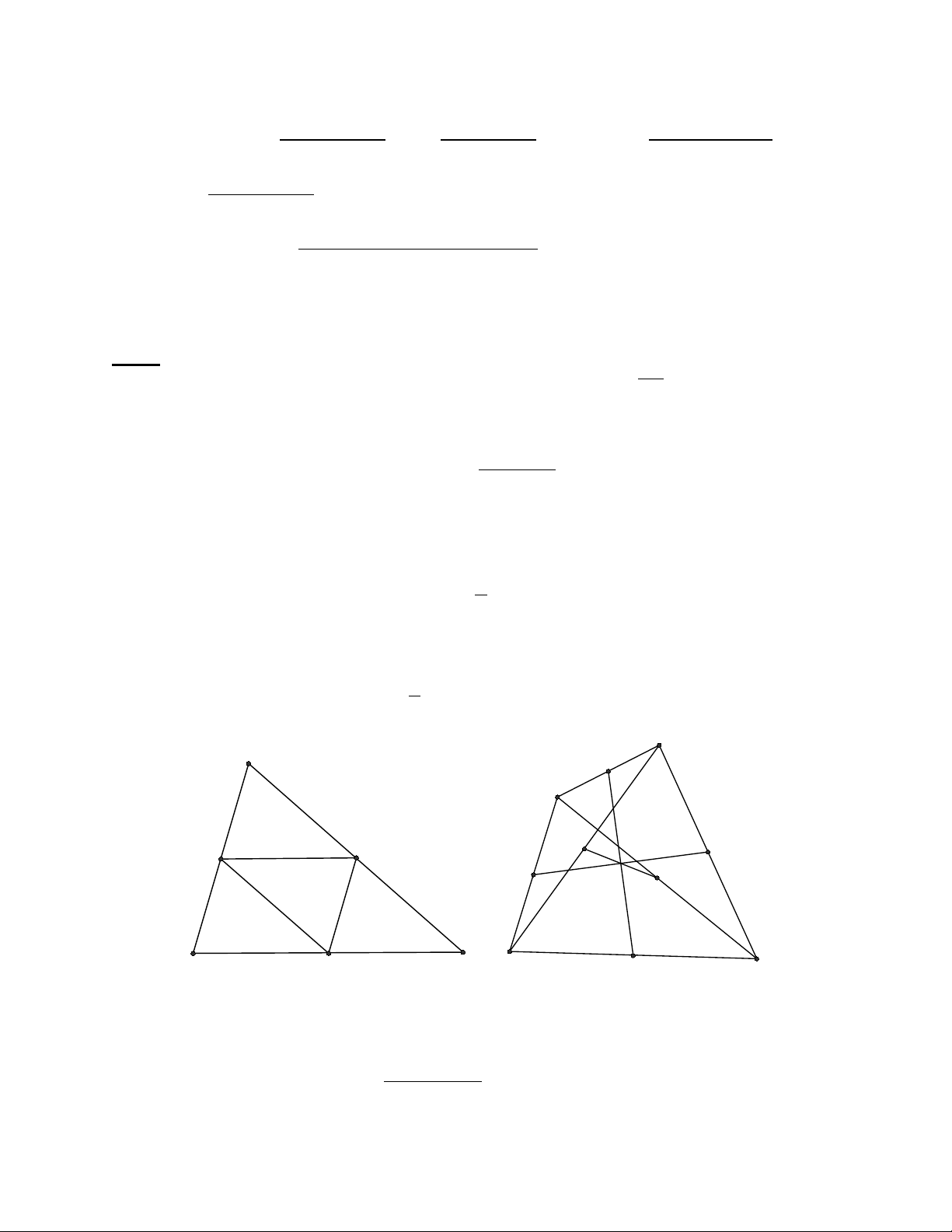
- Nếu M, N, P là trung điểm của các cạnh BC, CA, AB của tam giác ABC thì:
1()
2
MN NP PM AB BC CA++ = ++
.
- Nếu M, N, P, Q, R, S là trung điểm của các cạnh AB, CD, BC, DA, AC, BD của tứ giác ABCD
thì ta có bất đẳng thức sau:
1()
2
MN PQ RS AB BC CD DA AC BD++< +++++
P
N
M
A
B
C
N
P
S
Q
R
M
A
D
C
B
Áp dụng hai hệ thức trên cho tất cả các trung điểm. Ta thấy mỗi đoạn
,
ij
MM i j≠
bất kì đều
thuộc về một tam giác hoặc một tứ giác nào đó, còn mỗi cạnh
,
ij
AA i j≠
bất kì thì thuộc về
n – 2 tam giác hoặc thuộc về
2
2
( 2)( 3)
2
n
nn
C−
−−
=
tứ giác. Cộng từng vế các hệ thức đó, ta được:
4
2
11
1 1 32
( 2) ( 2)( 3)
24 4
i j ij
i jm i jn
nn
M M n n n AA M N
≤< ≤ ≤< ≤
−+

< −+ − − ⇔ <


∑∑
.
5
Bài 3. Trong mặt phẳng cho 3n điểm phân biệt
12 3
, ,... n
AA A
sao cho không có ba điểm nào
thẳng hàng và khoảng cách giữa 2 điểm bất kì không vượt quá 1. Chứng minh rằng:
1. Tồn tại đường thẳng d không đi qua bất cứ điểm nào trong các điểm
12 3
, ,... n
AA A
và
không song song với bất cứ đường thẳng chứa 2 điểm
,,
ij
AAi j≠
nào.
2. Giả sử khoảng cách từ các điểm
12 3
, ,... n
AA A
đến đường thẳng d tăng dần.
Chứng minh rằng các tam giác:
31 32 33
, 1,
ii i
AAA i n
++ +
=
đôi một rời nhau.
3. Chứng minh rằng tổng diện tích của n tam giác trên nhỏ hơn
1
2
.
Giải.
1. Gọi
Ω
là đa giác lồi chứa tất cả các điểm
12 3
, ,... n
AA A
. Kẻ một đường thẳng trong mặt phẳng
không cắt bất cứ cạnh nào của
Ω
thì đường thẳng này không đi qua điểm nào trong các điểm nói
trên. Do số điểm đã cho hữu hạn nên số đường thẳng qua 2 điểm bất kì cũng hữu hạn, vì vậy tồn
tại một đường thẳng không song song với bất cứ đường thẳng chứa 2 điểm nào trong 3n
điểmtrên.
Từ đó suy ra đường thẳng d tồn tại và ta có đpcm.
2. Qua các điểm
31i
A+
, kẻ các đường thẳng
i
∆
song song với d. Do khoảng cách từ các điểm
12 3
, ,...
n
AA A
đến d tăng dần nên các đường thẳng
i
∆
nói trên chia mặt phẳng thành các dãy mà
mỗi tam giác
31 32 33
, 1,
ii i
AAA i n
++ +
=
được phân cách với các tam giác khác bởi các đường thẳng
i
∆
. Tức là các tam giác nói trên rời nhau.
d
a
b
D
B
C
A
3. Gọi
, 1,
i
Si n=
là diện tích của tam giác
31 32 33ii i
AAA
++ +
. Rõ ràng tồn tại 2 đường thẳng a, b cùng
vuông góc với d và đi qua ít nhất 2 trong 3 đỉnh của tam giác
31 32 33ii i
AAA
++ +
. Qua đỉnh
33i
A+
, kẻ