Cơ học môi trường liên tục
CHƯƠNG V – LÝ THUYẾT ĐÀN HỒI
CHƯƠNG V – LÝ THUYẾT ĐÀN HỒI
CHƯƠNG V - LÝ THUYẾT ĐÀN HỒI
CHƯƠNG V - LÝ THUYẾT ĐÀN HỒI
Trong các chương trên ta đã nghiên cứu hai mặt riêng biệt của môi trường liên
Trong các chương trên ta đã nghiên cứu hai mặt riêng biệt của môi trường liên
tục đó là mặt tĩnh học (trường ứng suất) và mặt hình học (trường biến dạng), giữa
tục đó là mặt tĩnh học (trường ứng suất) và mặt hình học (trường biến dạng), giữa
hai mặt này có quan hệ với nhau. Sự phân bố ứng suất và biến dạng của môi
hai mặt này có quan hệ với nhau. Sự phân bố ứng suất và biến dạng của môi
trường phụ thuộc vào quan hệ đó. Xét quan hệ giữa ứng suất và biến dạng tức là
trường phụ thuộc vào quan hệ đó. Xét quan hệ giữa ứng suất và biến dạng tức là
xét về mặt vật lý của môi trường. Sự khác nhau về mặt vật lý đã dẫn đến những
xét về mặt vật lý của môi trường. Sự khác nhau về mặt vật lý đã dẫn đến những
nội dung khác nhau trong lý thuyết cơ học vật rắn biến dạng như lý thuyết đàn hồi
nội dung khác nhau trong lý thuyết cơ học vật rắn biến dạng như lý thuyết đàn hồi
tuyến tính, lý thuyết đàn hồi phi tuyến và lý thuyết đàn hồi dẻo.
tuyến tính, lý thuyết đàn hồi phi tuyến và lý thuyết đàn hồi dẻo.
Trong lý thuyết đàn hồi nói chung ứng suất là hàm của biến dạng :
Trong lý thuyết đàn hồi nói chung ứng suất là hàm của biến dạng :
σ
σx = f1(
x = f1(ε
εx,
x, ε
εy,
y, ε
εz,
z, γ
γxy,
xy, γ
γyz,
yz, γ
γzx);
zx);
σ
σy = f2(
y = f2(ε
εx,
x, ε
εy,...
y,... );
);
σ
σz = f3(
z = f3(ε
εx,
x, ε
εy,...
y,... );
);
Txy= f4(
Txy= f4(ε
εx,
x, ε
εy,...
y,... );
);
(5.1)
(5.1)
Tyz= f5(
Tyz= f5(ε
εx,
x, ε
εy,...
y,... );
);
Tzx= f6(
Tzx= f6(ε
εx,
x, ε
εy,...
y,... );
);
Cơ học môi trường liên tục Ths Phạm Văn Đạt
CHƯƠNG V – LÝ THUYẾT ĐÀN HỒI
CHƯƠNG V – LÝ THUYẾT ĐÀN HỒI
Cơ học môi trường liên tục
CHƯƠNG V – LÝ THUYẾT ĐÀN HỒI
CHƯƠNG V – LÝ THUYẾT ĐÀN HỒI
Trong môn học này ta giả thiết vật liệu làm việc đàn hồi tuyến tính tức quan hệ
Trong môn học này ta giả thiết vật liệu làm việc đàn hồi tuyến tính tức quan hệ
ứng suất và biến dạng là các quan hệ tuyến tính. Do đó (5.1) viết thành :
ứng suất và biến dạng là các quan hệ tuyến tính. Do đó (5.1) viết thành :
σ
σx = a11
x = a11ε
εx + a12
x + a12ε
εy + a13
y + a13ε
εz + a14
z + a14γ
γxy + a15
xy + a15γ
γyz + a16
yz + a16γ
γzx;
zx;
σ
σy = a21
y = a21ε
εx + a22
x + a22ε
εy + a23
y + a23ε
εz + a24
z + a24γ
γxy + a25
xy + a25γ
γyz + a26
yz + a26γ
γzx;
zx;
............
............ (5.2)
(5.2)
Tzx = a61
Tzx = a61ε
εx + a62
x + a62ε
εy + a63
y + a63ε
εz + a64
z + a64γ
γxy + a65
xy + a65γ
γyz + a66
yz + a66γ
γzx.
zx.
Trong đó :
Trong đó :
- Các hệ số aij : Là các hằng số đàn hồi của vật liệu.
- Các hệ số aij : Là các hằng số đàn hồi của vật liệu.
- Trong (5.2) : Có tất cả là 36 hằng số đàn hồi. Ta sẽ chứng minh rằng đối với
- Trong (5.2) : Có tất cả là 36 hằng số đàn hồi. Ta sẽ chứng minh rằng đối với
vật liệu hoàn toàn đàn hồi và đẳng hướng chỉ có 2 hằng số độc lập với nhau.
vật liệu hoàn toàn đàn hồi và đẳng hướng chỉ có 2 hằng số độc lập với nhau.
5.1 Công và thế của lực đàn hồi
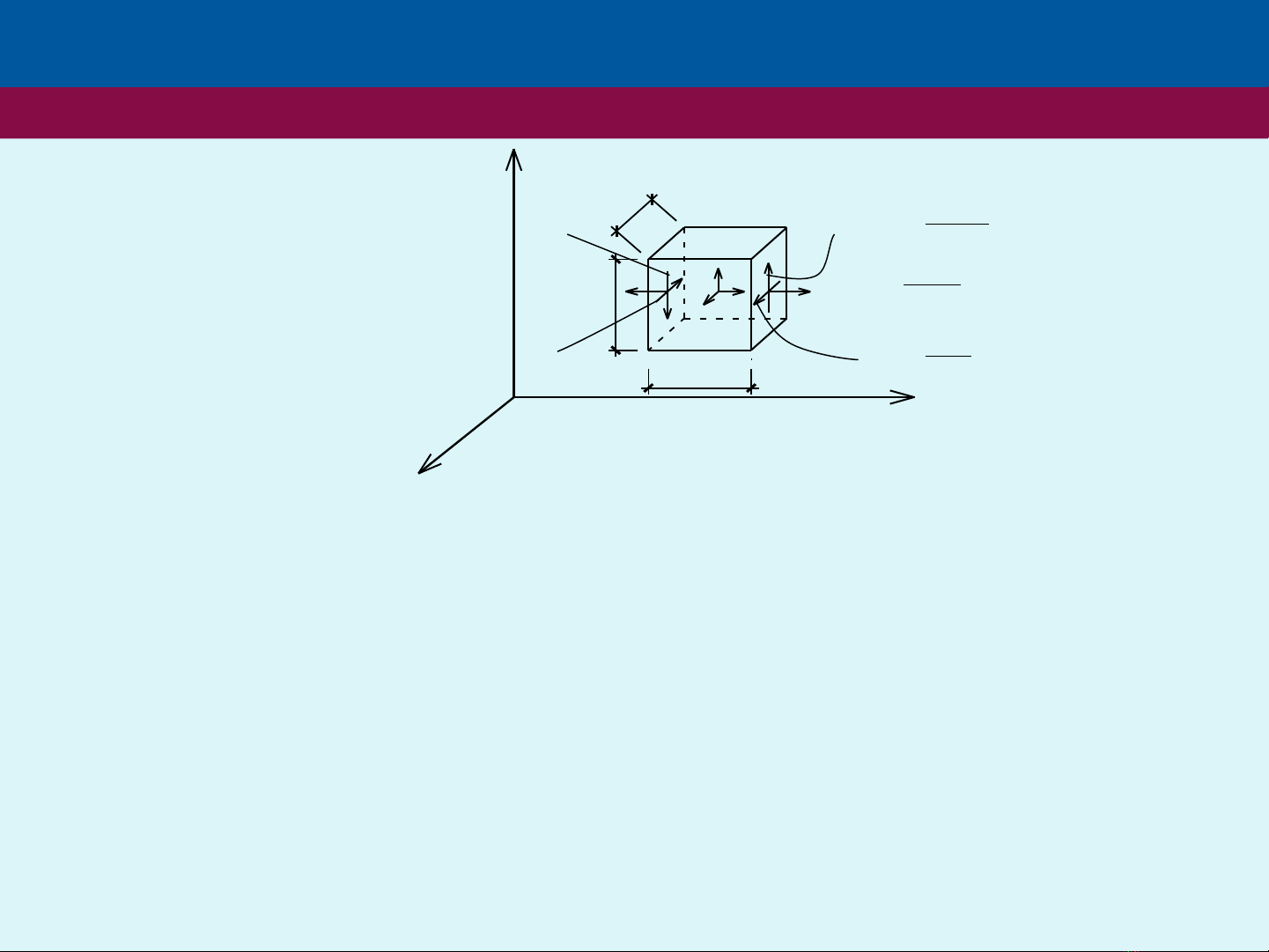
- Xét 1 phần tử hình hộp có các cạnh dx, dy, dz tại điểm M(x,y,z). Các mặt của
- Xét 1 phần tử hình hộp có các cạnh dx, dy, dz tại điểm M(x,y,z). Các mặt của
phân tử có các ứng suất như hình vẽ (H,5.1). Ứng với các ứng suất ấy phần
phân tử có các ứng suất như hình vẽ (H,5.1). Ứng với các ứng suất ấy phần
tử có chuyển vị đường và chuyển vị góc.
tử có chuyển vị đường và chuyển vị góc.
- Khi phần tử bị biến dạng các nội lực sinh ra một công.
- Khi phần tử bị biến dạng các nội lực sinh ra một công.
Cơ học môi trường liên tục
CHƯƠNG V – LÝ THUYẾT ĐÀN HỒI
CHƯƠNG V – LÝ THUYẾT ĐÀN HỒI
dx
x
x
x
∂
∂
+
σ
σ
dx
x
xy
xy
∂
∂
+
τ
τ
dx
x
xz
xz
∂
∂
+
τ
τ
z
x
y
dx
dy
dz
P(x,y+dy,z)
N(x+dx,y,z)
Q(x,y,z+dz)
τxy
σx
τxy
5.1.1. Số gia của công do ứng suất pháp sinh ra:
5.1.1. Số gia của công do ứng suất pháp sinh ra:
- Ứng suất pháp trên 2 mặt vuông góc trục x là :
- Ứng suất pháp trên 2 mặt vuông góc trục x là : σ
σx và
x và σ
σx + .dx, có độ
x + .dx, có độ
dài tương đối
dài tương đối ε
εx, độ dãn dài tuyệt đối :
x, độ dãn dài tuyệt đối : ε
εx.dx.
x.dx.
- Sau thời gian vô cùng bé
- Sau thời gian vô cùng bé δ
δt, phân tố có độ dài tương đối thêm số gia:
t, phân tố có độ dài tương đối thêm số gia:
δε
δεx. Số gia của độ dãn dài tuyệt đối của cạnh dx :
x. Số gia của độ dãn dài tuyệt đối của cạnh dx : δε
δεx .dx.
x .dx.
Số gia của công do
Số gia của công do σ
σx sinh ra : (
x sinh ra : (σ
σx.dydz)(
x.dydz)( δε
δεx.dx)
x.dx)
Tương tự số gia của công
Tương tự số gia của công σ
σy và
y và σ
σz sinh ra :
z sinh ra :
(
(σ
σy.dxdz)(
y.dxdz)( δε
δεy .dy)
y .dy)
(a)
(a)
(
(σ
σz.dxdy)(
z.dxdy)( δε
δεy .dz).
y .dz).
Cơ học môi trường liên tục
CHƯƠNG V – LÝ THUYẾT ĐÀN HỒI
CHƯƠNG V – LÝ THUYẾT ĐÀN HỒI
5.1.2. Số gia của công do ứng suất tiếp sinh ra:
5.1.2. Số gia của công do ứng suất tiếp sinh ra:
- Xét thành phần Txy ở tại thời điểm t, góc trượt tỷ đối là
- Xét thành phần Txy ở tại thời điểm t, góc trượt tỷ đối là γ
γxy. Sau thời gian
xy. Sau thời gian δ
δt,
t,
góc trượt đó có số gia
góc trượt đó có số gia δγ
δγxy.
xy.
- Lực do Txy : Txy.dy.dz.
- Lực do Txy : Txy.dy.dz.
- Moment do Txy tác dụng trên 2 mặt phẳng đối diện vuông góc ox :
- Moment do Txy tác dụng trên 2 mặt phẳng đối diện vuông góc ox :
(Txy.dydz).dx.
(Txy.dydz).dx.
- Số gia của công do Txy sinh ra : (Txy.dydz.dx).
- Số gia của công do Txy sinh ra : (Txy.dydz.dx). δγ
δγxy.
xy.
-Tương tự số gia của công do các ứng suất tiếp Tyz và Tzx sinh ra là :
Tương tự số gia của công do các ứng suất tiếp Tyz và Tzx sinh ra là :
(Tyz.dzdx.dy).
(Tyz.dzdx.dy). δγ
δγxz.
xz. (b)
(b)
(Tzx.dxdy.dz).
(Tzx.dxdy.dz). δγ
δγzx.
zx.
- Số gia công của phần tử hình hộp bằng tổng số gia của công do các ứng suất
- Số gia công của phần tử hình hộp bằng tổng số gia của công do các ứng suất
sinh ra (a+b):
sinh ra (a+b):
δ
δT = (
T = (σ
σx.
x. δε
δεx +
x +σ
σy.
y. δε
δεy +
y +σ
σz.
z. δε
δεz +Txy
z +Txyδγ
δγxy + Tyz
xy + Tyzδγ
δγyz + zx
yz + zxδγ
δγzx )dxdydz. (5.3)
zx )dxdydz. (5.3)
Ta có: dV = dxdydz : Thể tích của phần tử trước biến dạng.
Ta có: dV = dxdydz : Thể tích của phần tử trước biến dạng.
*Số gia của công của một đơn vị thể tích (công riêng)
*Số gia của công của một đơn vị thể tích (công riêng) δ
δA sẽ là :
A sẽ là :
δ
δA = =
A = = σ
σx.
x. δε
δεx +
x +σ
σy.
y. δε
δεy +
y +σ
σz.
z. δε
δεz +Txy
z +Txyδγ
δγxy + Tyz
xy + Tyzδγ
δγyz + Tzx
yz + Tzxδγ
δγzx (5.4)
zx (5.4)
Cơ học môi trường liên tục
CHƯƠNG V – LÝ THUYẾT ĐÀN HỒI
CHƯƠNG V – LÝ THUYẾT ĐÀN HỒI
* Đối với vật thể hoàn toàn đàn hồi năng lượng sinh ra do biến dạng được
* Đối với vật thể hoàn toàn đàn hồi năng lượng sinh ra do biến dạng được
bảo toàn. Nếu gọi
bảo toàn. Nếu gọi W
W là thế năng biến dạng đàn hồi tích lũy khi vật thể biến
là thế năng biến dạng đàn hồi tích lũy khi vật thể biến
dạng thì độ lớn của thế năng biến dạng đàn hồi bằng công ngoại lực A.
dạng thì độ lớn của thế năng biến dạng đàn hồi bằng công ngoại lực A.
Do vậy ta có
Do vậy ta có A = W
A = W (5.5)
(5.5)
Lực đàn hồi thỏa mãn điều kiện (5.5) gọi là có thế .
Lực đàn hồi thỏa mãn điều kiện (5.5) gọi là có thế .
Từ (5.5)
Từ (5.5) ⇔
⇔
δ
δA =
A = δ
δW
W(5.6)
(5.6)
Thế năng sinh ra do biến dạng và chỉ do biến dạng mà có, vì vậy
Thế năng sinh ra do biến dạng và chỉ do biến dạng mà có, vì vậy
thế năng biến dạng đàn hồi là hàm số của các thành phần biến dạng :
thế năng biến dạng đàn hồi là hàm số của các thành phần biến dạng :
W = f(
W = f(ε
εx,
x, ε
εy,
y, ε
εz,
z, γ
γxy,
xy, γ
γyz,
yz, γ
γzx).
zx).
- Trong miền đàn hồi quá trình biến dạng là thuận nghịch nên
- Trong miền đàn hồi quá trình biến dạng là thuận nghịch nên δ
δW là 1 vi
W là 1 vi
phân toàn phần. Nếu bỏ qua các vô cùng bé bậc cao khi khai triển số gia
phân toàn phần. Nếu bỏ qua các vô cùng bé bậc cao khi khai triển số gia
của thế năng biến dạng đàn hồi theo biến dạng ta được :
của thế năng biến dạng đàn hồi theo biến dạng ta được :
)75( −
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
=
zx
zx
yz
yz
xy
xy
z
z
y
y
x
x
WWWWWW
W
δγ
γ
δγ
γ
δγ
γ
δε
ε
δε
ε
δε
ε
δ