08/01/2024 22:08 81
TS. Lương Văn Hải
CHƯƠNG 4. QUAN HỆ ỨNG SUẤT VÀ BIẾN DẠNG
4.1. Định luật Hooke tổng quát
4.2. Quan hệ giữa ứng suất tiếp và biến dạng trượt trên mặt bát diện
4.3. Định luật Hooke khối
4.4. Thế năng biến dạng đàn hồi
4.5. Các hằng số đàn hồi của vật liệu
4.6. Các phương trình cơ bản của lý thuyết đàn hồi
4.7. Định lý về sự duy nhất nghiệm
Sinh viên tự đọc
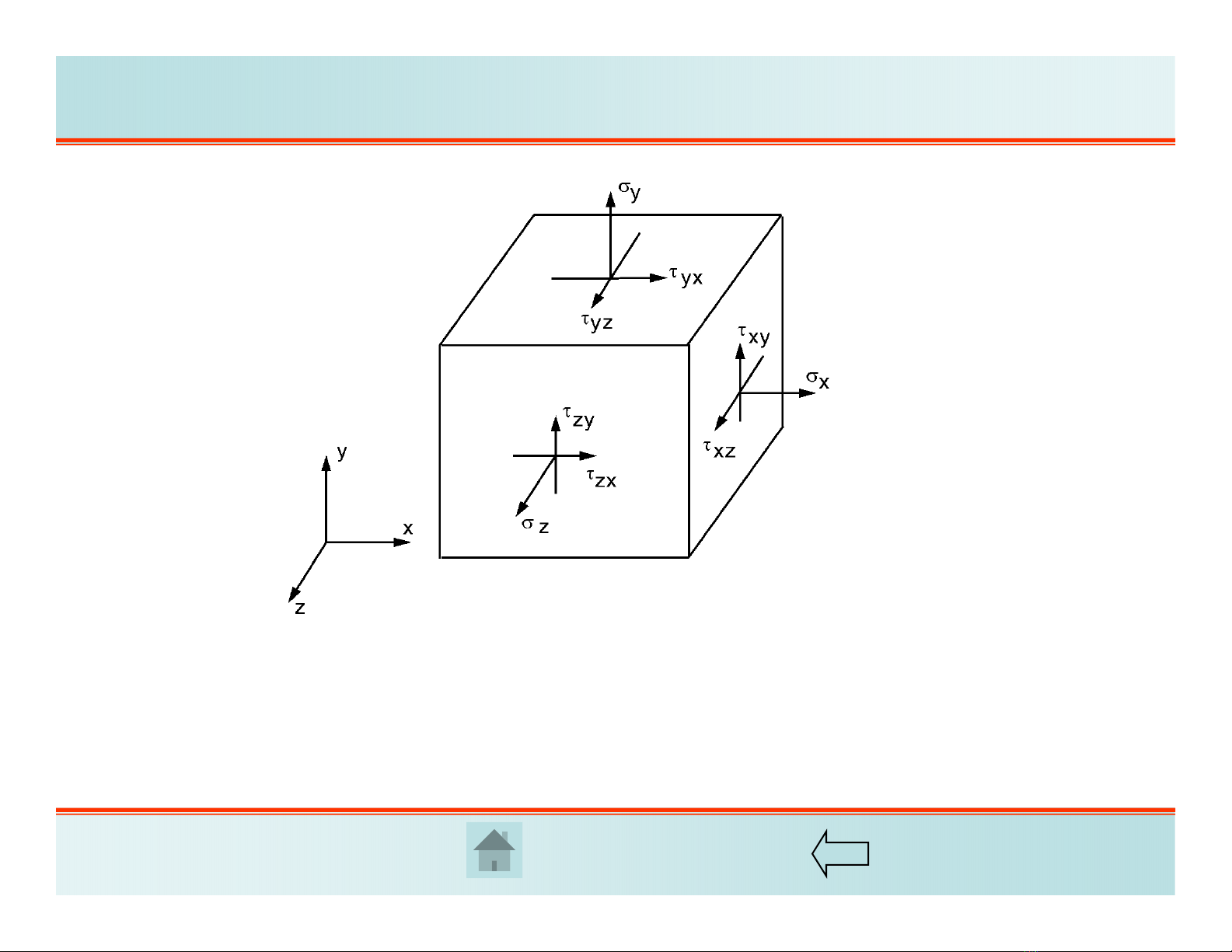
4.1. ĐỊNH LUẬT HOOKE TỔNG QUÁT
08/01/2024 22:08 82
TS. Lương Văn Hải
Sáu thành phần ứng suất
x,
y,
z,
xy,
yz,
zx và sáu thành phần biến dạng
x,
y,
z,
xy,
yz,
zx
4.1. ĐỊNH LUẬT HOOKE TỔNG QUÁT
08/01/2024 22:08 83
TS. Lương Văn Hải
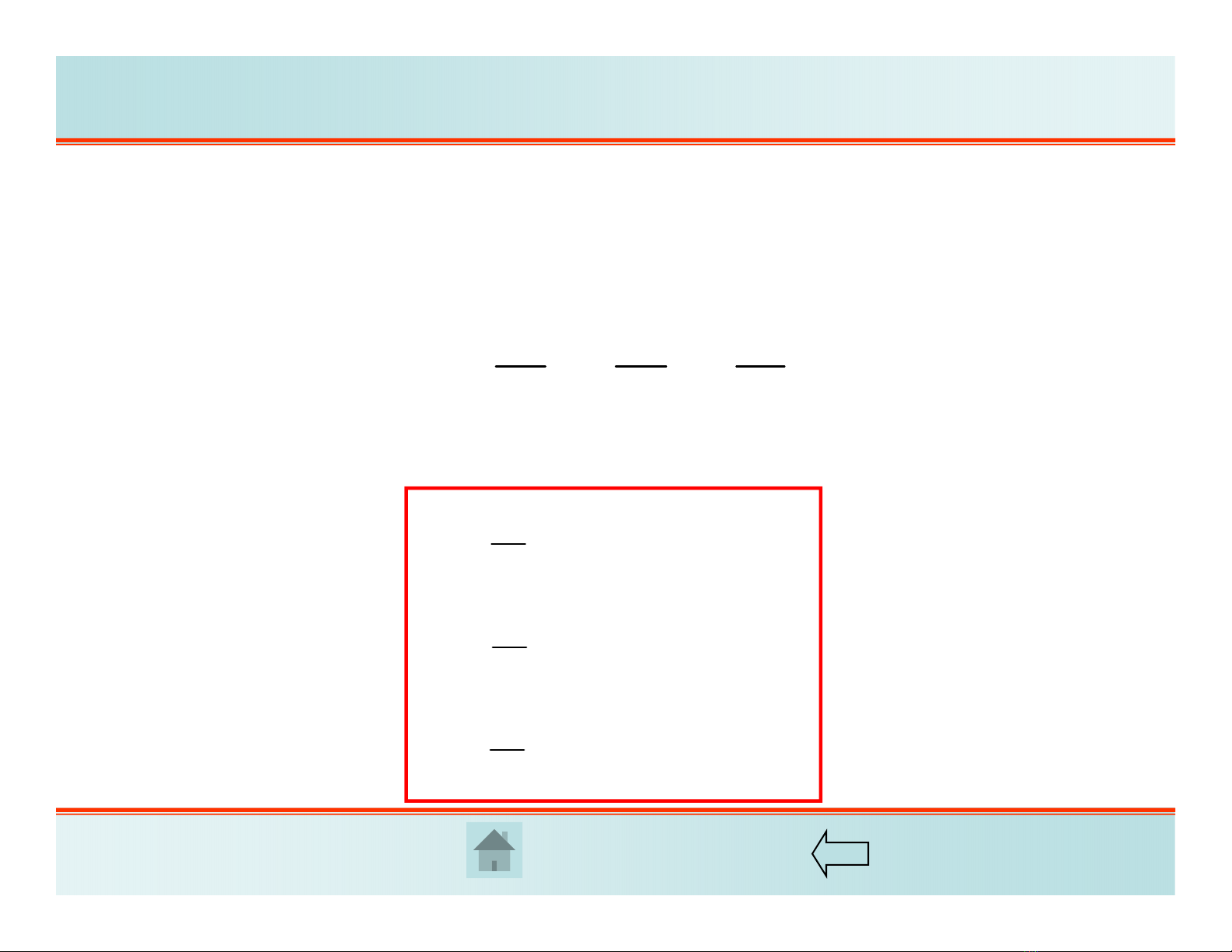
Định luật Hooke trường hợp đơn
x
xx xy xz

y
x
z
x
E
EE
 
trong đó Elà mô đun đàn hồi và
là hệ số Poisson của vật liệu
1
1
1
()
()
()
x
xyz
yyxz
z
zxy
E
E
E



4.1. ĐỊNH LUẬT HOOKE TỔNG QUÁT
08/01/2024 22:08 84
TS. Lương Văn Hải
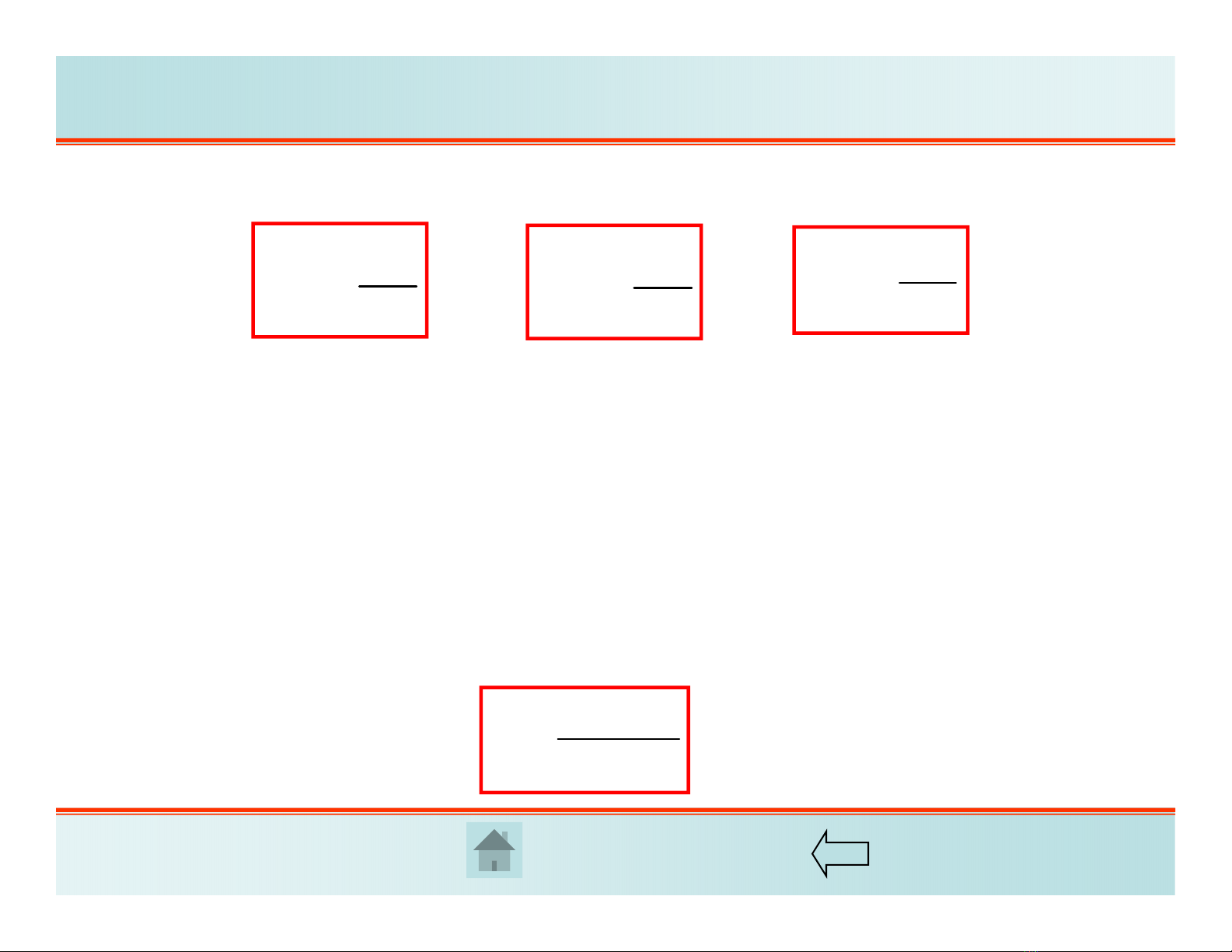
Ứng suất tiếp chỉ gây ra biến dạng góc trong mặt phẳng mà nó tác dụng:
trong đó Glà mô đun đàn hồi trượt
x
y
xy G

y
z
yz G

z
x
zx G

Công thức trên cho thấy với vật liệu đồng nhất và đẳng hướng, nếu các ứng suất
tiếp bằng 0 thì các biến dạng góc cũng bằng 0. Như vậy, các phương chính của
tensor ứng suất trùng với các phương chính của tensor biến dạng.
Đối với vật liệu đàn hồi đẳng hướng, chỉ có 2 hằng số vật liệu độc lập. Quan hệ giữa
hằng số E,
và Gcó phương trình:
21()
E
G
4.1. ĐỊNH LUẬT HOOKE TỔNG QUÁT
08/01/2024 22:08 85
TS. Lương Văn Hải
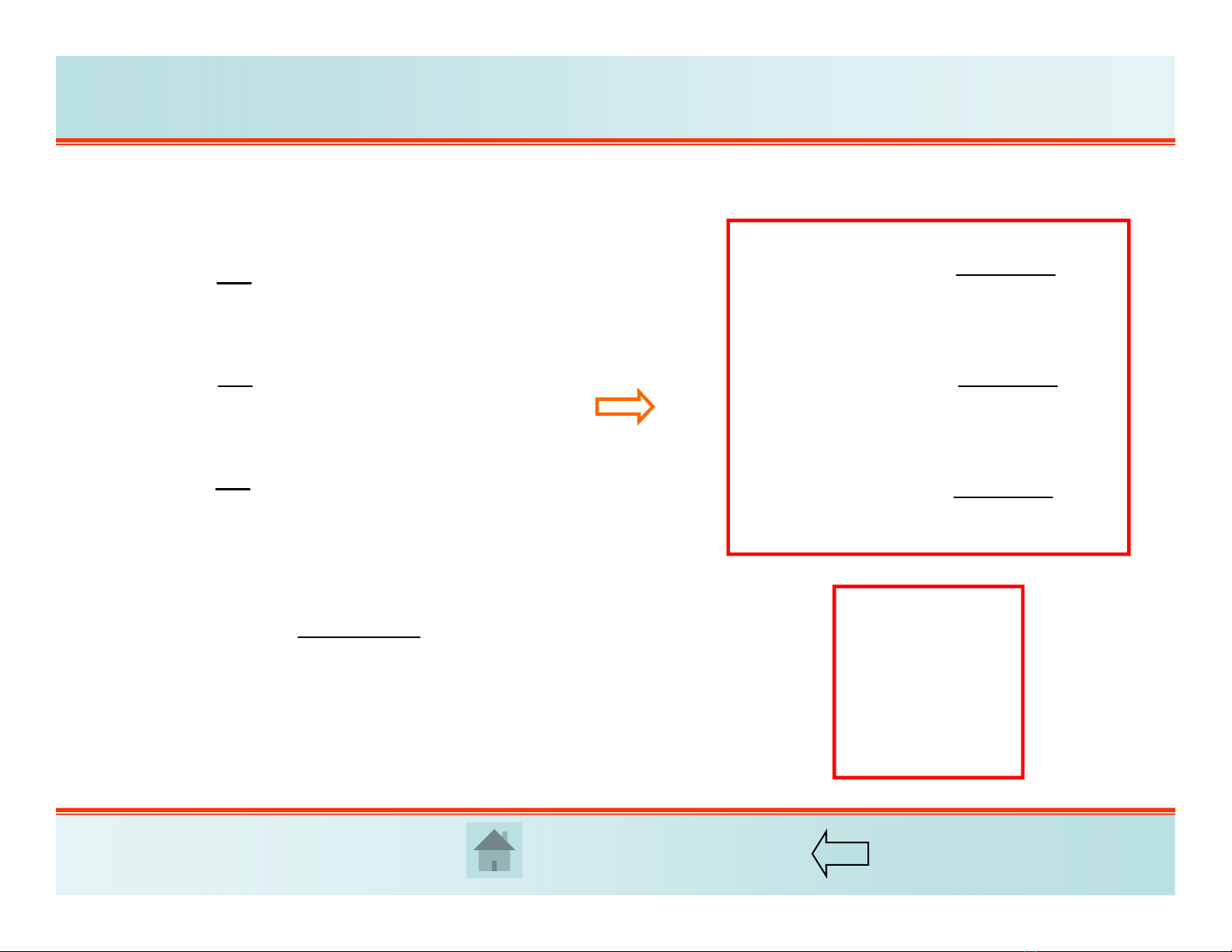
Ta có:
21()
E
G
3
212
3
212
3
212
()
()
()
x
xtb
yy tb
z
ztb
G
G
G






x
yxy
yz yz
z
xzx
G
G
G



1
1
1
()
()
()
x
xyz
yyxz
z
zxy
E
E
E








