3.4 Khái niệm về tensor cầu và độ lệch tensor biến dạng
3.1. Các thành phần biến dạng và tensor biến dạng
3.2 Quan hệ giữa biến dạng và chuyển vị
3.3 Trạng thái biến dạng tại một điểm
08/01/2024 22:08 60
TS. Lương Văn Hải
CHƯƠNG 3. LÝ THUYẾT BIẾN DẠNG
3.5 Các phương trình liên tục về biến dạng
3.1. CÁC THÀNH PHẦN VÀ TENSOR BIẾN DẠNG
08/01/2024 22:08 61
TS. Lương Văn Hải
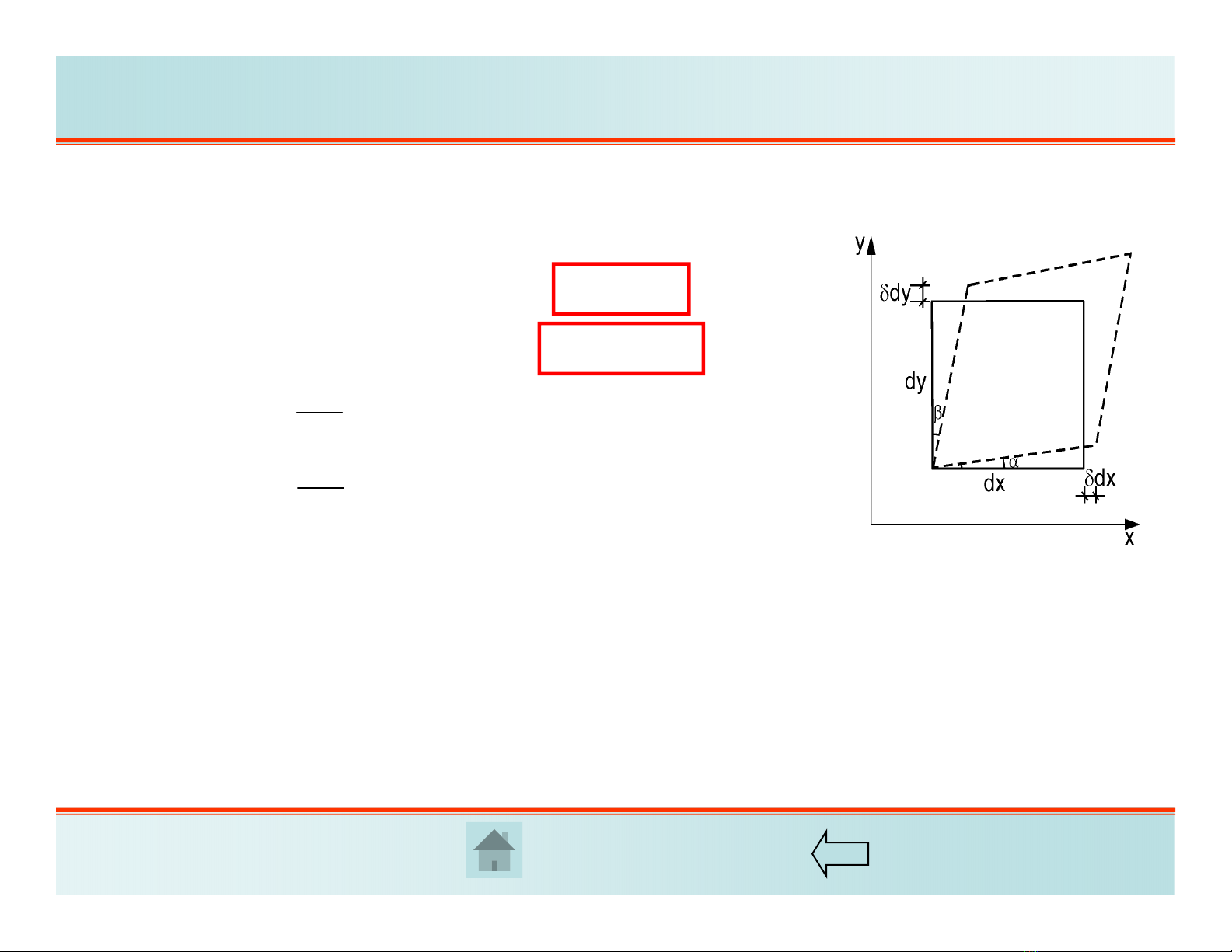
Nếu tách một phân tố hình hộp VCB trong hệ trục tọa độ xyz thì biến dạng có thể phân
tích thành 6 thành phần độc lập:
+ 3 thành phần biến dạng dài
+ 3 thành phần biến dạng góc
,,
x
yz

,,
x
yyzzx

trong đó x
y
dx
dx
d
y
d
y
xy

Biến dạng dài
được qui ước là dương khi phân tố thẳng dãn dài và âm khi co ngắn.
Biến dạng góc được định nghĩa là sự thay đổi góc vuông. Biến dạng góc được qui
ước là dương khi làm giảm góc vuông ban đầu.
3.1. CÁC THÀNH PHẦN VÀ TENSOR BIẾN DẠNG
08/01/2024 22:08 62
TS. Lương Văn Hải
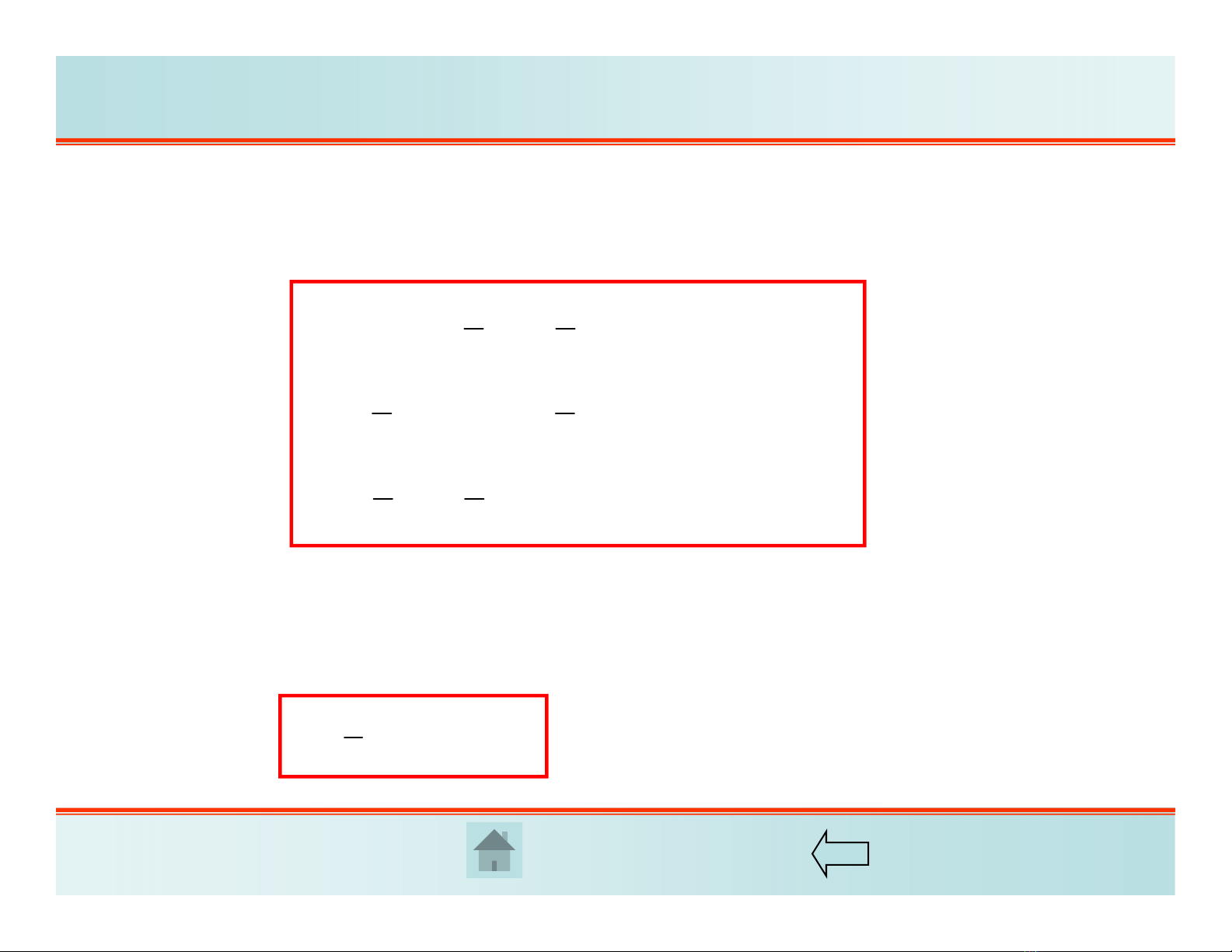
Tương tự như ứng suất, biến dạng tại một điểm cũng là một đại lượng tensor biến dạng
hạng 2 đối xứng, gồm 6 thành phần độc lập:
11 12 13
21 22 23
31 32 33
11
22
11
22
11
22









xxyxz
yx y yz
zx zy z
T





Cách viết chỉ số được dùng khi áp dụng phép tính tensor để thể hiện và suy diễn các
phương trình về biến dạng.
Lưu ý:

1
2
ij ij ij


3.2. QUAN HỆ GIỮA BIẾN DẠNG VÀ CHUYỂN VỊ
08/01/2024 22:08 63
TS. Lương Văn Hải
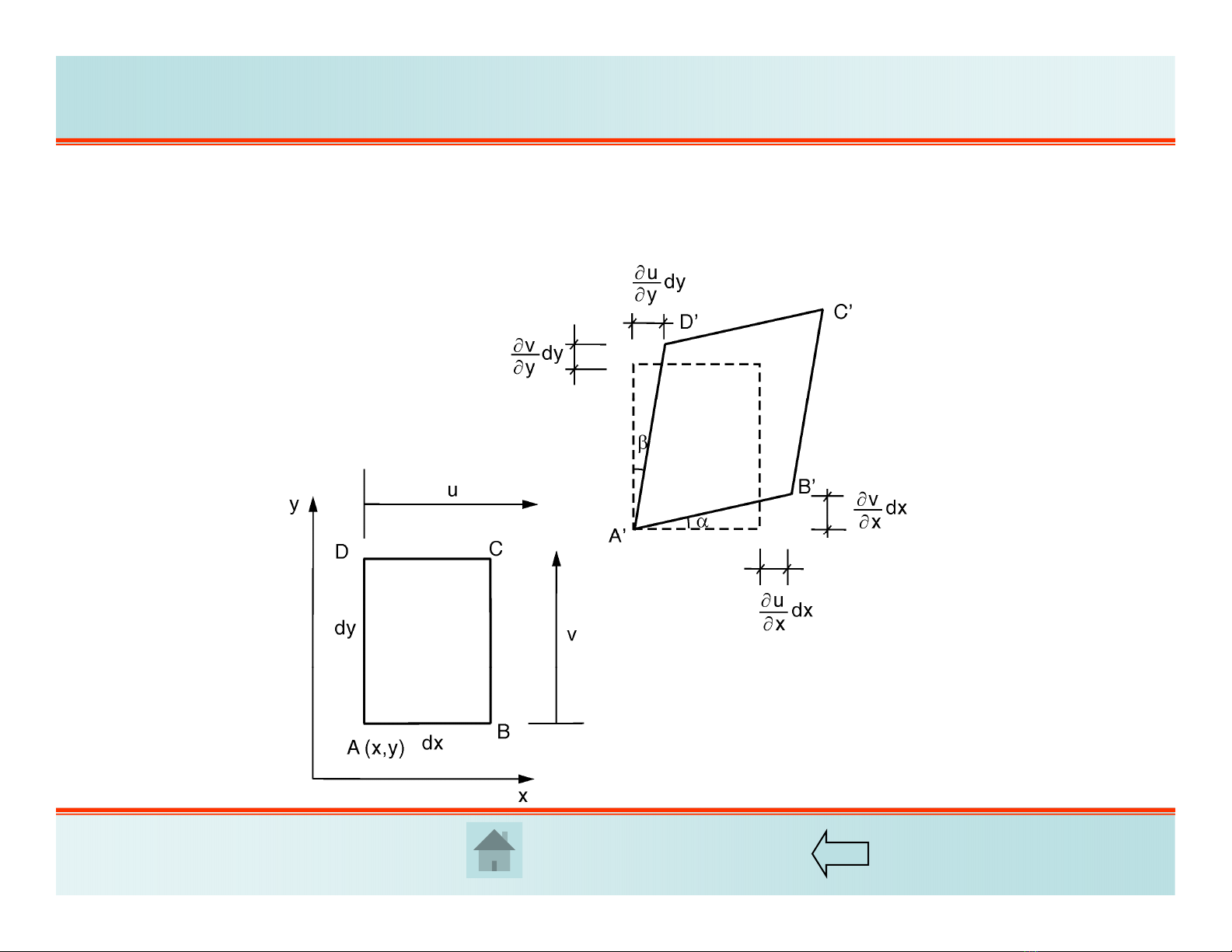
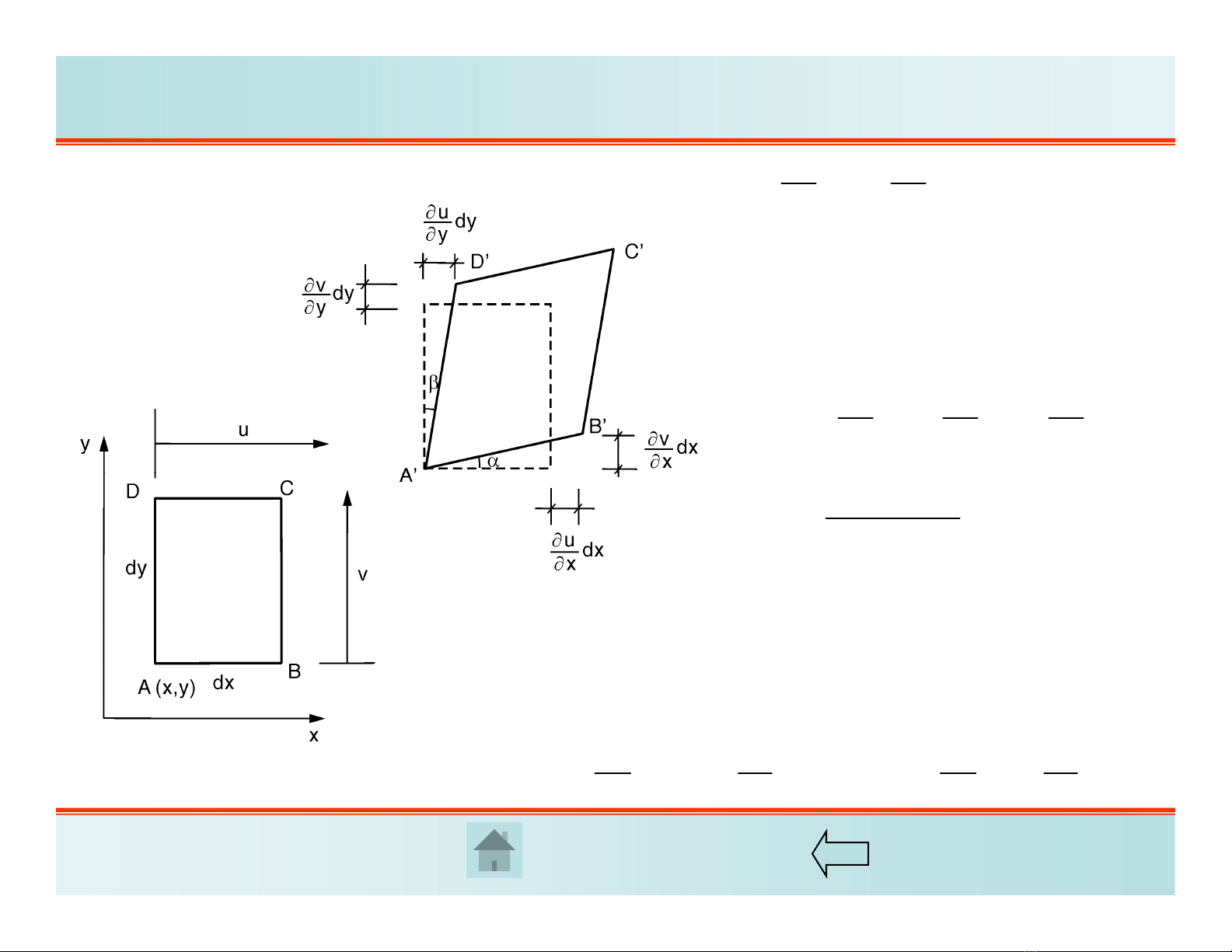
Kí hiệu chuyển vị của một điểm theo ba trục tọa độ x, y, z lần lượt là u, v, w. Biến dạng
phẳng ta có w = 0, do đó u = u(x,y); v = v(x,y)
3.2. QUAN HỆ GIỮA BIẾN DẠNG VÀ CHUYỂN VỊ
08/01/2024 22:08 64
TS. Lương Văn Hải
Vi phân toàn phần của hàm hai biến f(x,y): (,) ff
df x y dx dy
xy


Sự thay đổi của chuyển vị tại B
so với A là (dy=0):
uuu
du dx dy dx
xyx



x
AB AB
AB

11()()
xx
A
BABdx

 
Suy ra: 222
1()( )
x
A
Bdx
 


 



222222
1()( )( )( )()
uv uv
A
Bdxdx dx dx
xx xx
Hình học ta có: