
08/01/2024 22:08 235
TS. Lương Văn Hải
CHƯƠNG 9. NGUYÊN LÝ NĂNG LƯỢNG & BIẾN PHÂN
9.1. Đặt vấn đề
9.2. Các khái niệm: công, công bù, thế năng và thế năng bù
9.3. Nguyên lý thế năng toàn phần
9.4. Nguyên lý thế năng bù
9.5. Các phương pháp biến phân. Phương pháp Rayleigh-Ritz
9.1. ĐẶT VẤN ĐỀ
08/01/2024 22:08 236
TS. Lương Văn Hải
Các nguyên lý năng lượng cho một hướng khác để giải bài toán
LTĐH, bằng cách cực tiểu hóa một biểu thức năng lượng nào đó, thay
vì giải phương trình vi phân.
Các phương pháp này sử dụng lý thuyết biến phân, một ngành của
toán học liên quan đến cực trị của các tích phân (phiếm hàm), nên còn
được gọi là các phương pháp biến phân.
Dưới đây sẽ trình nguyên lý thế năng toàn phần và nguyên lý thế năng
bù toàn phần, làm cơ sở cho các phương pháp biến phân.
9.2. CÁC KHÁI NIỆM: CÔNG, CÔNG BÙ, THẾ NĂNG VÀ THẾ NĂNG BÙ
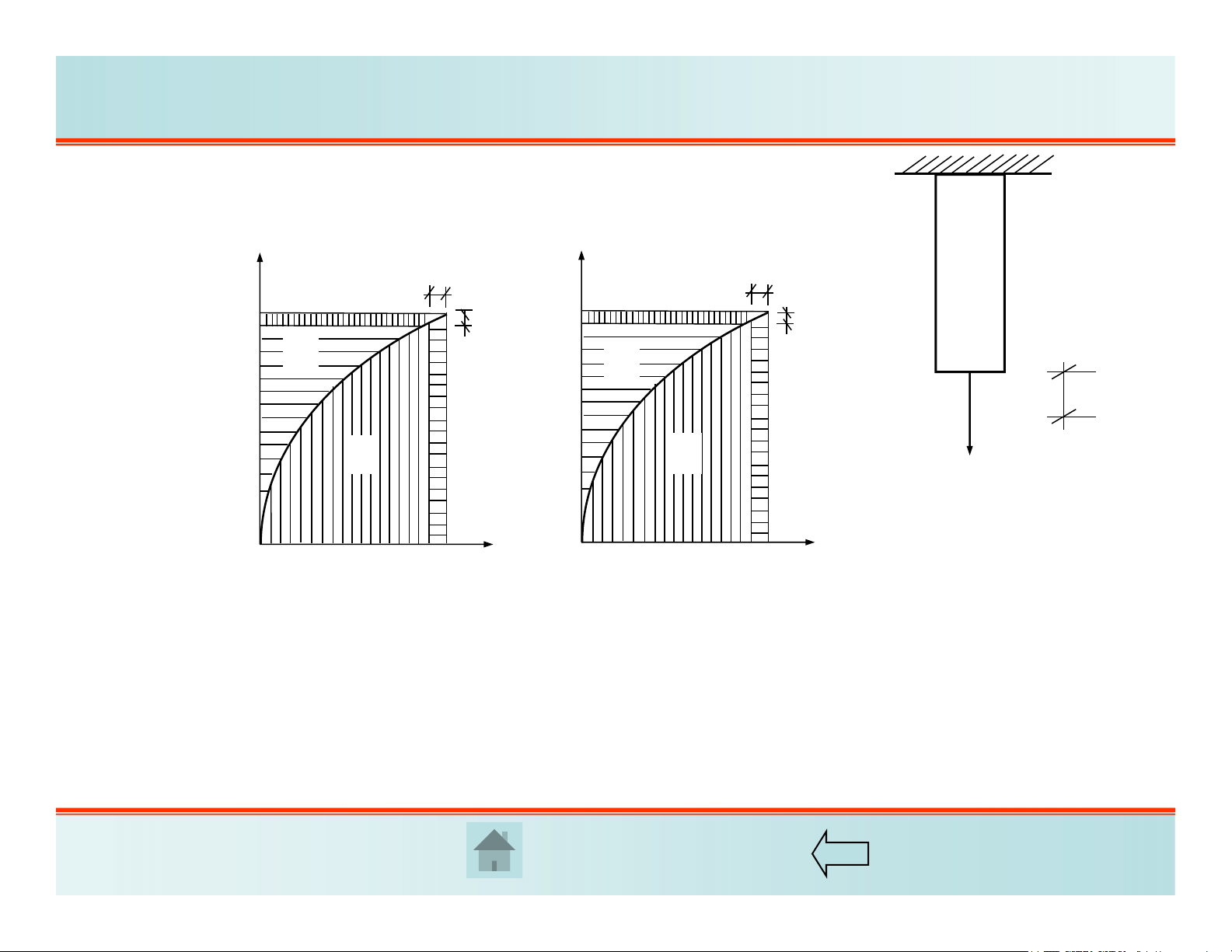
Một thanh chịu kéo bởi lực P và có chuyển vị Δ.
Giả sử quan hệ P-Δ và tương ứng là
P
P
P
W
W*
W
W*
u
u*
u
u*
P
Công, công bù của ngoại lực:
0
WPd
P
=diện tích dưới đường cong
*
0
P
WdP
P
diện tích trên đường cong
08/01/2024 22:08 237
TS. Lương Văn Hải
9.2. CÁC KHÁI NIỆM: CÔNG, CÔNG BÙ, THẾ NĂNG VÀ THẾ NĂNG BÙ
Thế năng riêng, bù biến dạng đàn hồi:
0
ud
= diện tích dưới đường cong
*
0
ud
= diện tích trên đường cong
P
Nếu lực P có sự thay đổi - còn gọi là biến phân của lực thì tương
ứng ta sẽ có biến phân của chuyển vị .
Khi ấy ta sẽ có các đại lượng biến phân:
-Biến phân của công:
-Biến phân của công bù:
-Biến phân thế năng riêng:
- Biến phân thế năng riêng bù:
WP
*
WP
*
W
còn gọi là công khả dĩ
u
*
u
08/01/2024 22:08 238
TS. Lương Văn Hải
9.2. CÁC KHÁI NIỆM: CÔNG, CÔNG BÙ, THẾ NĂNG VÀ THẾ NĂNG BÙ
Có nhiều lực tương ứng với nhiều chuyển vị , nhiều thành phần
ứng suất tương ứng với nhiều biến dạng thì:
i
Pi
i
j
i
j
*
*
...
...
ii
ii
x
xyy zxzx
x
xyy zxzx
WP
WP
u
u
Thế năng và thế năng bù toàn vật thể: **
;
VV
UudVU udV
Nếu đàn hồi tuyến tính thì **
;uuUU
08/01/2024 22:08 239
TS. Lương Văn Hải












![Bài giảng Quản lý vận hành và bảo trì công trình xây dựng [chuẩn nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20251006/agonars97/135x160/30881759736164.jpg)









![Ngân hàng câu hỏi trắc nghiệm Sức bền vật liệu 1: [Mô tả/Định tính Thêm để Tăng CTR]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250920/kimphuong1001/135x160/6851758357416.jpg)


![Trắc nghiệm Kinh tế xây dựng [chuẩn nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250920/kimphuong1001/135x160/32781758338877.jpg)
