08/01/2024 22:08 257
TS. Lương Văn Hải
10.1 Giới thiệu phương pháp
10.2 Dàn phẳng
10.3 Dầm và khung phẳng
10.4 Bài toán phẳng với phần tử tam giác
CHƯƠNG 10. PHƯƠNG PHÁP PHẦN TỬ HỮU HẠN
10.1 GIỚI THIỆU PHƯƠNG PHÁP
08/01/2024 22:08 258
TS. Lương Văn Hải
Để giải bài toán đàn hồi, chọn ẩn số cơ bản là ứng suất (phương
pháp lực) hoặc chuyển vị theo (phương pháp chuyển vị).
Chương này trình bày PP PTHH theo mô hình tương thích, trong đó
ẩn số cơ bản cần tìm là các thành phần chuyển vị nút. Đây là mô hình
được phát triển hoàn thiện và áp dụng rộng rãi nhất hiện nay…
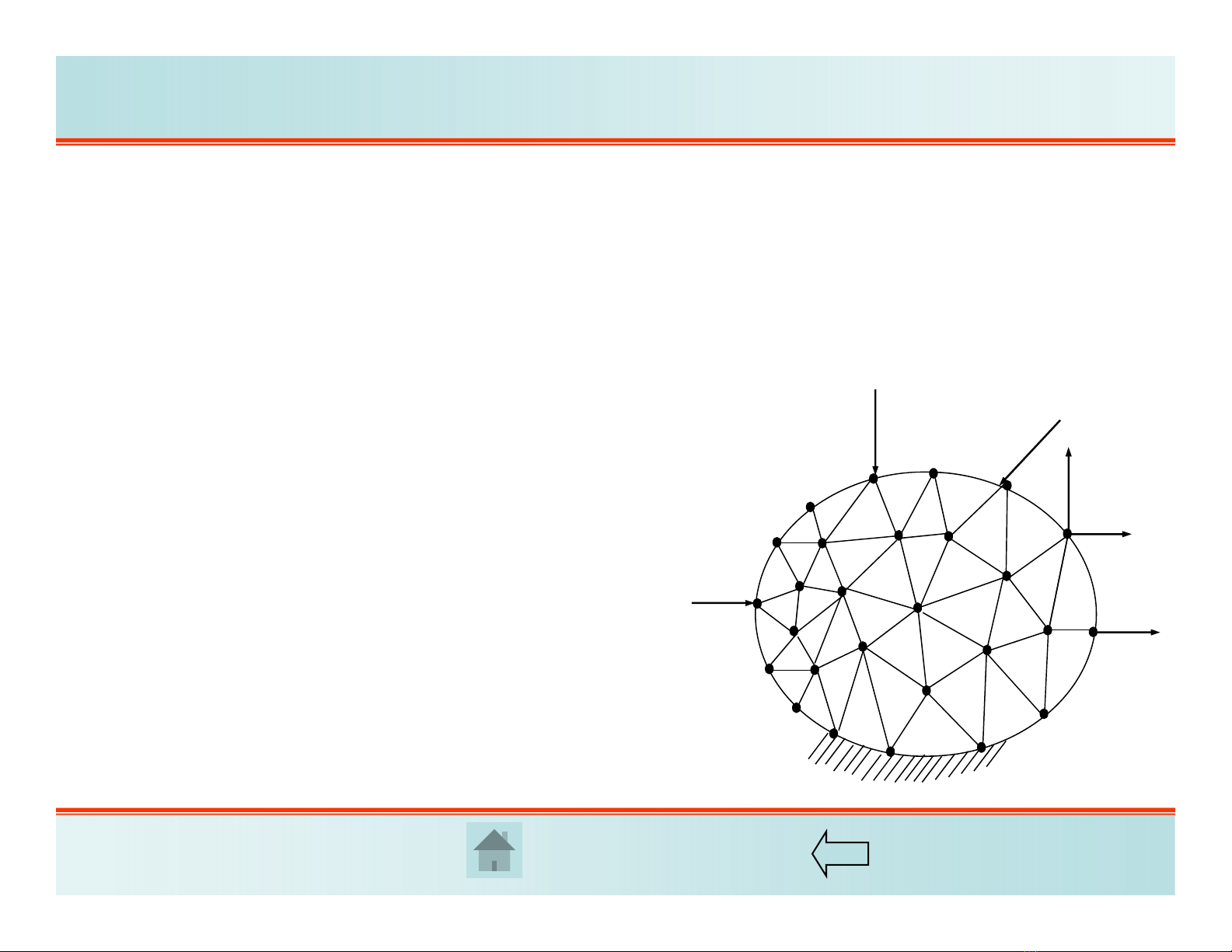
PP PTHH có thể coi như là sự mở rộng
của phương pháp chuyển vị trong Cơ
kết cấu từ hệ thanh sang các dạng kết
cấu khác như vách, tấm, vỏ, vật thể
dạng khối. Trường chuyển vị trong
mỗi phần tử được xấp xỉ bởi các hàm
chọn trước và các chuyển vị nút đóng
vai trò là ẩn số của bài toán.
10.1 GIỚI THIỆU PHƯƠNG PHÁP
Các hàm chọn trước được gọi là các hàm dạng hoặc hàm nộisuy,
ảnh hưởng đến độ chính xác của lời giải; thường chúng được chọn là
các đa thức để đơn giản hóa về toán học.
Dùng các phương trình của LTĐH ta sẽ tìm được mối quan hệ giữa
chuyển vị nút và lực nút thông qua ma trận cứng của phần tử, từ đó
ma trận cứng của toàn hệ được xây dựng tương tự như phương pháp
chuyển vị trong Cơ học kết cấu.
Chuyển vị của các nút được tìm từ điều kiện cân bằng nút trên toàn hệ
cùng điều kiện biên động học, sau đó suy ra biến dạng và ứng suất.
Phần dưới đây sẽ trình bày bảnchấtvà trình tựcủa PP PTHH thông
qua dàn phẳng, khung phẳng, bài toán phẳng LTĐH.
08/01/2024 22:08 259
TS. Lương Văn Hải
10.2 DÀN PHẲNG
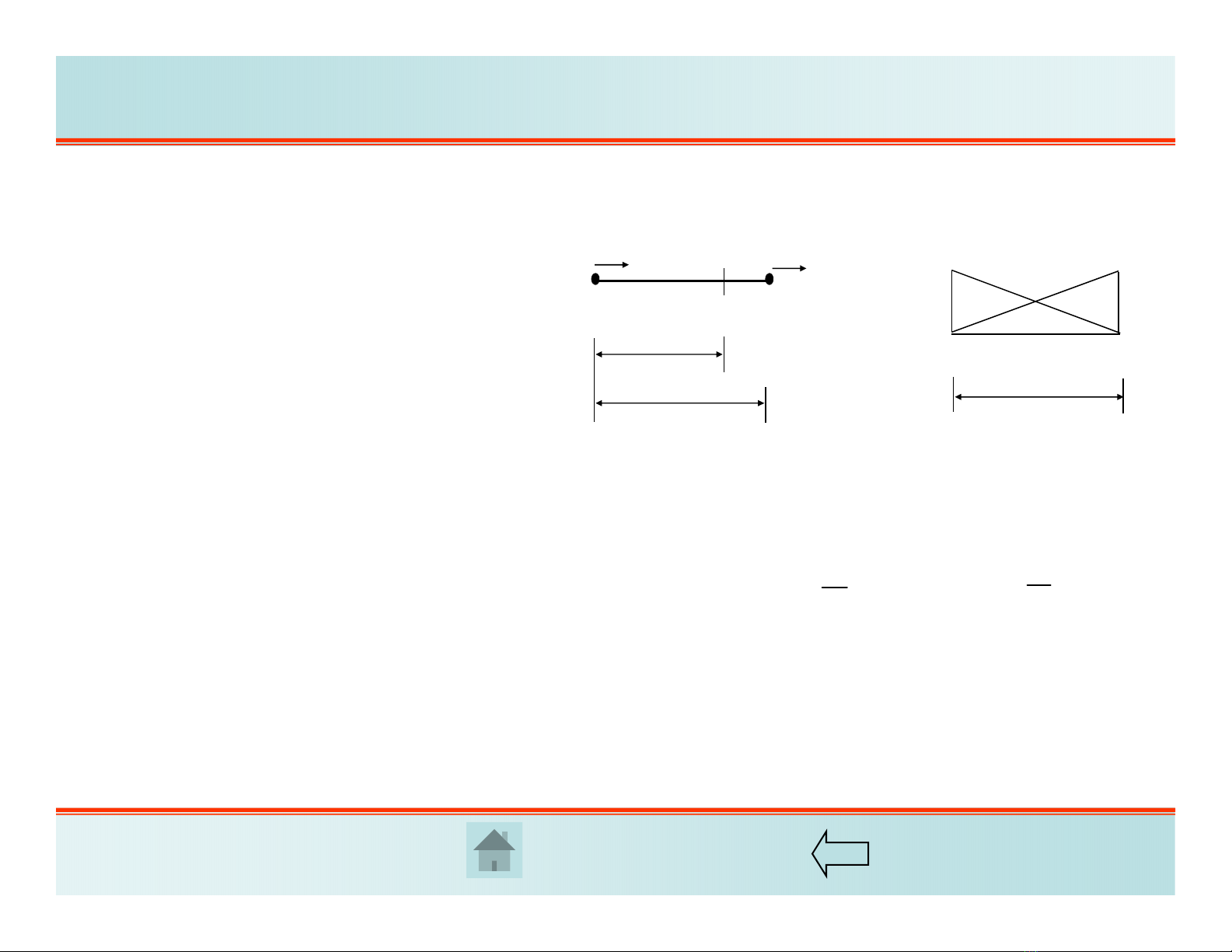
10.2.1 Ma trận cứng phần tử
1- Trong tọa độ địa phương
ij
x
L
K
ui,
Pi
uj,
Pj11
N1(x
)
N2(x)
L
ij
a) Chuyển vị và lực nút b) Các hàm dạng
Giả thiết chuyển vị Klà hàm
bậc nhất tọa độ:
12
()ux a ax
biểu diễn chuyển vị theo các
chuyển vị nút và các
hàm bậc nhất :
ji uu ,
)(),( 21 xNxN
12
() () ()
ij
ux uN x uN x trong đó: 1() 1
x
Nx
L
 2() x
Nx L
Cáchàmnàyđượcgọilàhàmdạng(shape functions) hoặc hàm nội
suy (interpolation functions), có tác dụng xấp xỉ trường chuyển vị
trong phần tử theo các chuyển vị nút.
08/01/2024 22:08 260
TS. Lương Văn Hải
10.2 DÀN PHẲNG
Nếu thế x=0 và x=L, ta thu được: 11
12 2
10
1
i
j
uaa
uaaL La






 


Phương trình có thể viết lại:
{}
[]
{}
ee
uAa
trong đó: 10
[] 1
AL



do đó: 1
10
[] 11
A
L
L
Phương trình viết như sau: 12
() [ () ()] i
j
u
ux N x N x u
 () [ ]{}
e
ux N u
12
[][ () ()]NNxNx
với : ma trận các hàm dạng
Như vậy, trường chuyển vị trong một phần tử dù chọn dưới dạng đa
thức (10.1) nhưng cuối cùng cũng biểu diễn được theo các hàm dạng
và các chuyển vị nút.
08/01/2024 22:08 261
TS. Lương Văn Hải