2.1. Các thành phần ứng suất và qui ước dấu
08/01/2024 22:08 22
TS. Lương Văn Hải
CHƯƠNG 2. LÝ THUYẾT ỨNG SUẤT
2.2. Các phương trình vi phân cân bằng
2.3. Điều kiện biên
2.4. Trạng thái ứng suất tại một điểm
2.5. Ứng suất chính và các bất biến của ứng suất
2.6. Ứng suất tiếp lớn nhất 2.7. Ứng suất bát diện
2.8. Tensor cầu và độ lệch của tensor ứng suất
2.9. Khái niện về tensor và dạng chỉ số của các phương trình LTĐH
2.1. CÁC THÀNH PHẦN ỨNG SUẤT VÀ QUI ƯỚC DẤU
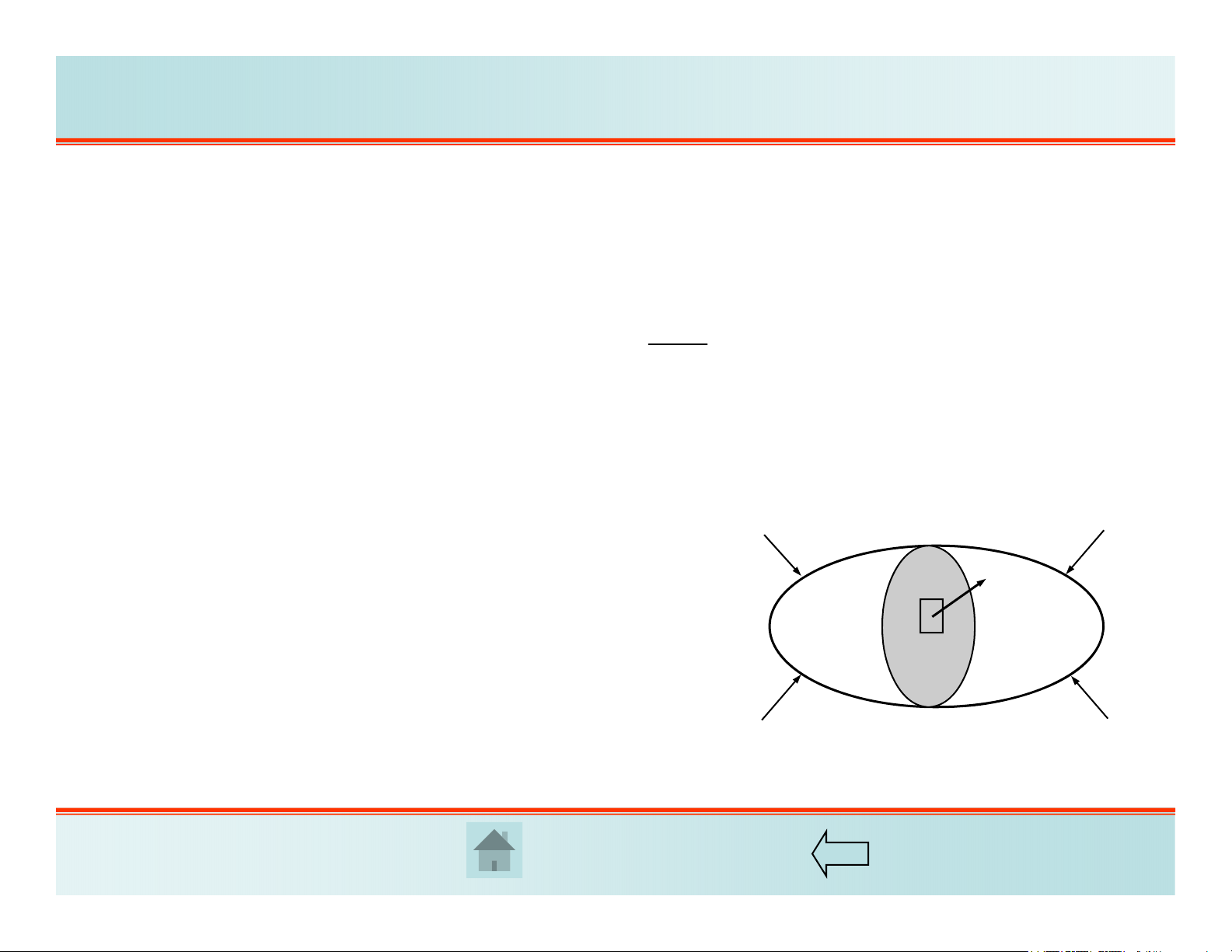
Ứng suất toàn phần tại một điểm trong vật thể trên một mặt nghiêng nào đó (H.2.1)
được định nghĩa bởi phương trình:
08/01/2024 22:08 23
TS. Lương Văn Hải
0
lim
A
F
p
A
F : vi phân hợp lực
A : vi phân diện tích bao quanh một điểm của phần vật thể được xét
F
A
Ứng suất ptại một điểm được xác định khi
biết trị số, phương chiều và bề mặt mà nó
tác dụng.
Hình 2.1. Định nghĩa ứng suất tại một điểm
2.1. CÁC THÀNH PHẦN ỨNG SUẤT VÀ QUI ƯỚC DẤU
Về mặt toán học, ứng suất tại một điểm được mô tả bằng một tensor hạng 2 gọi là
tensor ứng suấtvà được kí hiệu là T
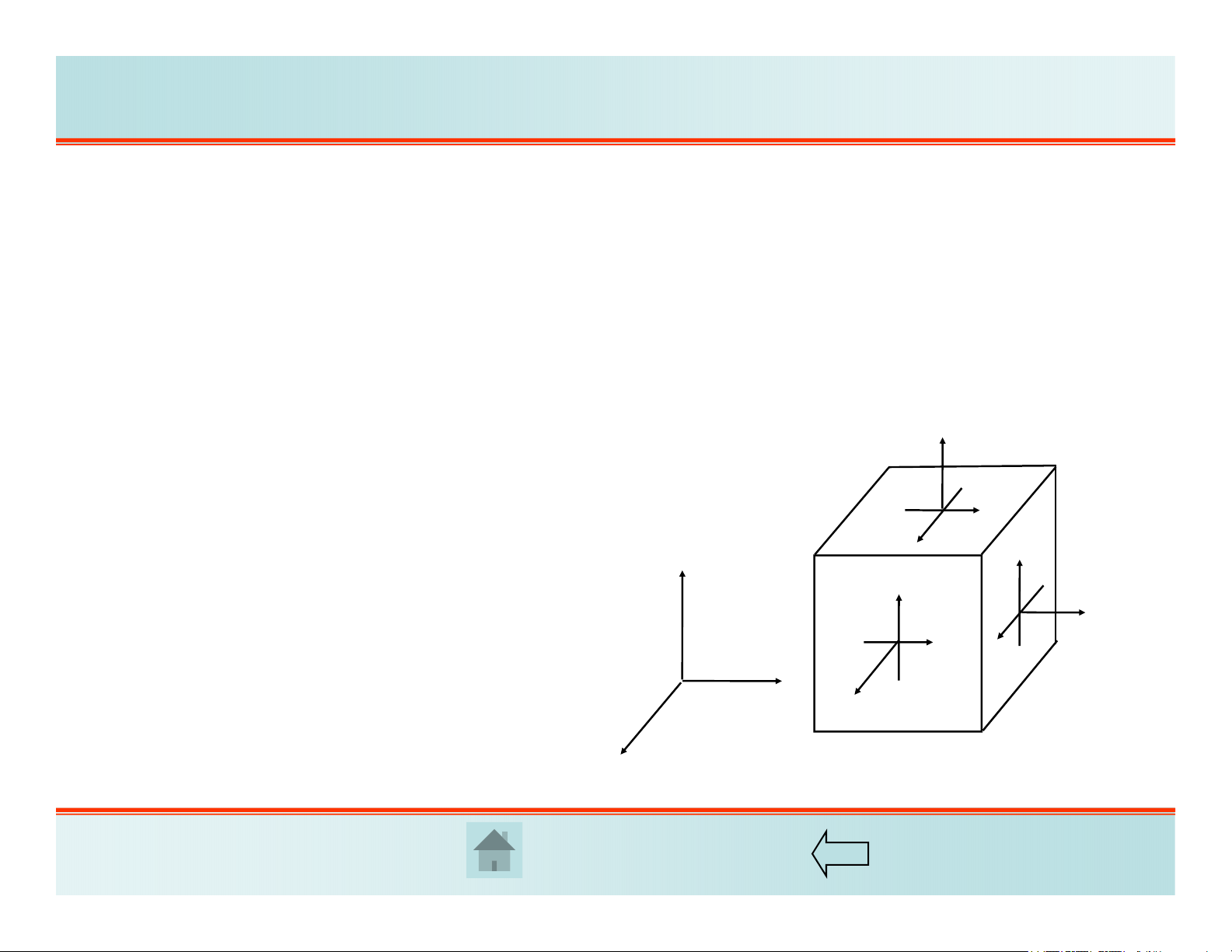
Nếu tách từ vật thể một phân tố hình hộp vô cùng bé, thì các thành phần ứng suất tác
động trên các mặt:
08/01/2024 22:08 24
TS. Lương Văn Hải
y
x
z
yx
yz
xy
zy
zx
xz
y
x
z
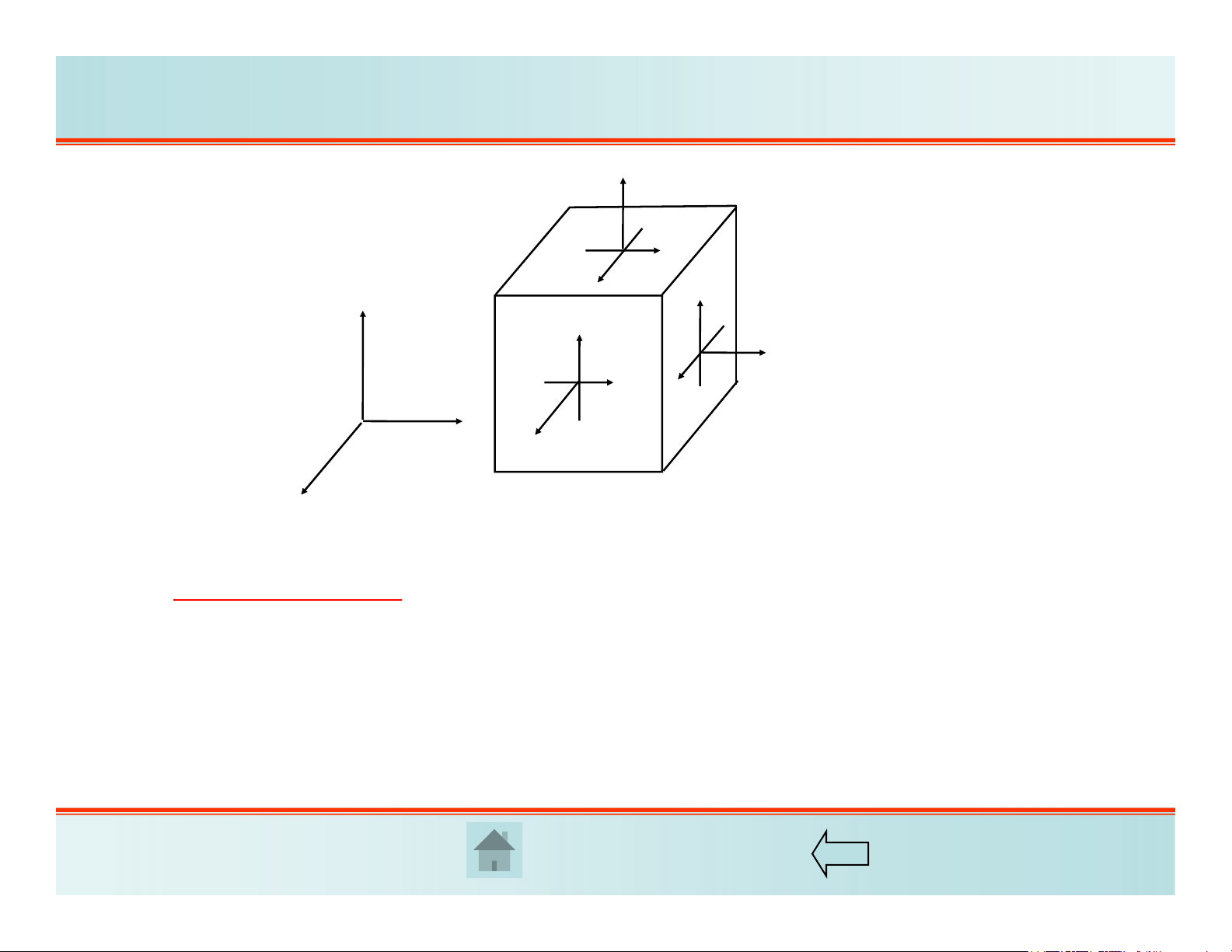
Hình 2.2. Các thành phần ứng suất
Có tất cả 9 thành phần ứng suất, gồm:
-Ba ứng suất pháp x, y, z
-Sáu ứng suất tiếp xy, yx, yz, zy, zx, xz
2.1. CÁC THÀNH PHẦN ỨNG SUẤT VÀ QUI ƯỚC DẤU
08/01/2024 22:08 25
TS. Lương Văn Hải
y
x
z
yx
yz
xy
zy
zx
xz
y
x
z
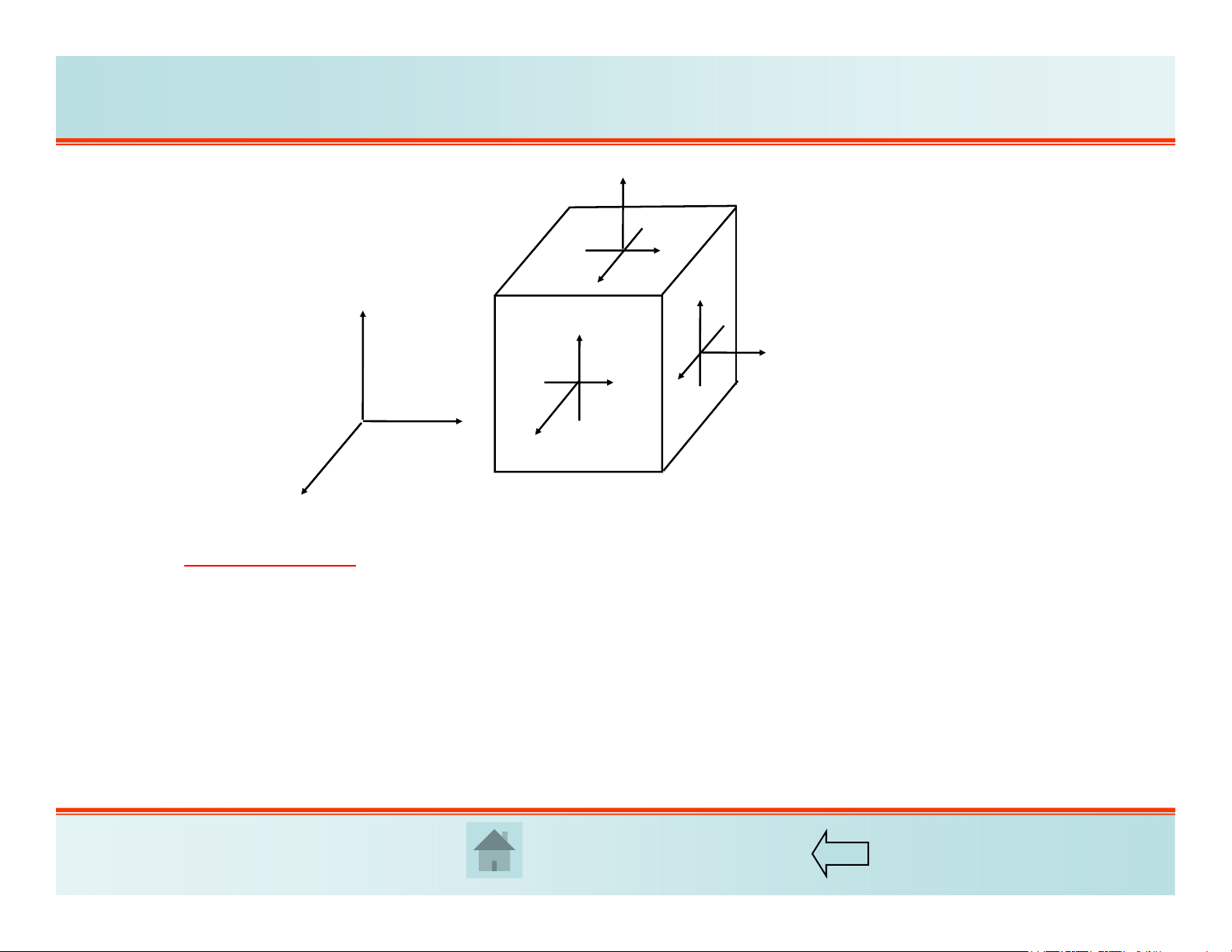
Hình 2.2. Các thành phần ứng suất
Có hai chỉ số:
- Chỉ số thứ nhất thể hiện pháp tuyến của bề mặt mà ứng suất đó tác dụng
- Chỉ số thứ hai thể hiện phương tác dụng
Kí hiệu để chỉ ứng suất pháp, để chỉ ứng suất tiếp
xlà ứng suất pháp trên mặt có pháp tuyến x(bỏ bớt một chỉ số xcho
gọn)
xy là ứng suất tiếp theo phương ytrên mặt có pháp tuyến theo phương x
2.1. CÁC THÀNH PHẦN ỨNG SUẤT VÀ QUI ƯỚC DẤU
08/01/2024 22:08 26
TS. Lương Văn Hải
y
x
z
yx
yz
xy
zy
zx
xz
y
x
z
Hình 2.2. Các thành phần ứng suất
Định luật đối ứng:
xy = yx, yz = zy, zx = xz
Vậy chỉ có sáu thành phần ứng suất độc lập












![Bài giảng Quản lý vận hành và bảo trì công trình xây dựng [chuẩn nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20251006/agonars97/135x160/30881759736164.jpg)









![Ngân hàng câu hỏi trắc nghiệm Sức bền vật liệu 1: [Mô tả/Định tính Thêm để Tăng CTR]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250920/kimphuong1001/135x160/6851758357416.jpg)


![Trắc nghiệm Kinh tế xây dựng [chuẩn nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250920/kimphuong1001/135x160/32781758338877.jpg)
