
08/01/2024 22:08 108
TS. Lương Văn Hải
CHƯƠNG 5. BT PHẲNG TỌA ĐỘ VUÔNG GÓC
5.1. Khái niệm bài toán phẳng
5.2. Thiết lập phương trình chủ đạo
5.3. Các đường lối giải bài toán LTĐH
5.4. Phương pháp đa thức – đường lối ngược
5.5. Đường lối nửa ngược
5.6. Phương pháp chuỗi lượng giác Sinh viên tự đọc
5.1. KHÁI NIỆM BÀI TOÁN PHẲNG
08/01/2024 22:08 109
TS. Lương Văn Hải
Với bài toán không gian, việc giải hệ các phương trình là rất phức tạp, và dường như
không thực hiện được trong trường hợp tổng quát do các khó khăn về mặt toán học.
Tuy nhiên, thực tế có nhiều bài toán có thể giải được nếu bổ sung một số giả thiếtđơn
giản hóa, trong số đó có thể kể đến các bài toán phẳng.
Hai dạng bài toán bài toán phẳng:
Ứng suất phẳng Biến dạng phẳng
5.1. KHÁI NIỆM BÀI TOÁN PHẲNG
08/01/2024 22:08 110
TS. Lương Văn Hải
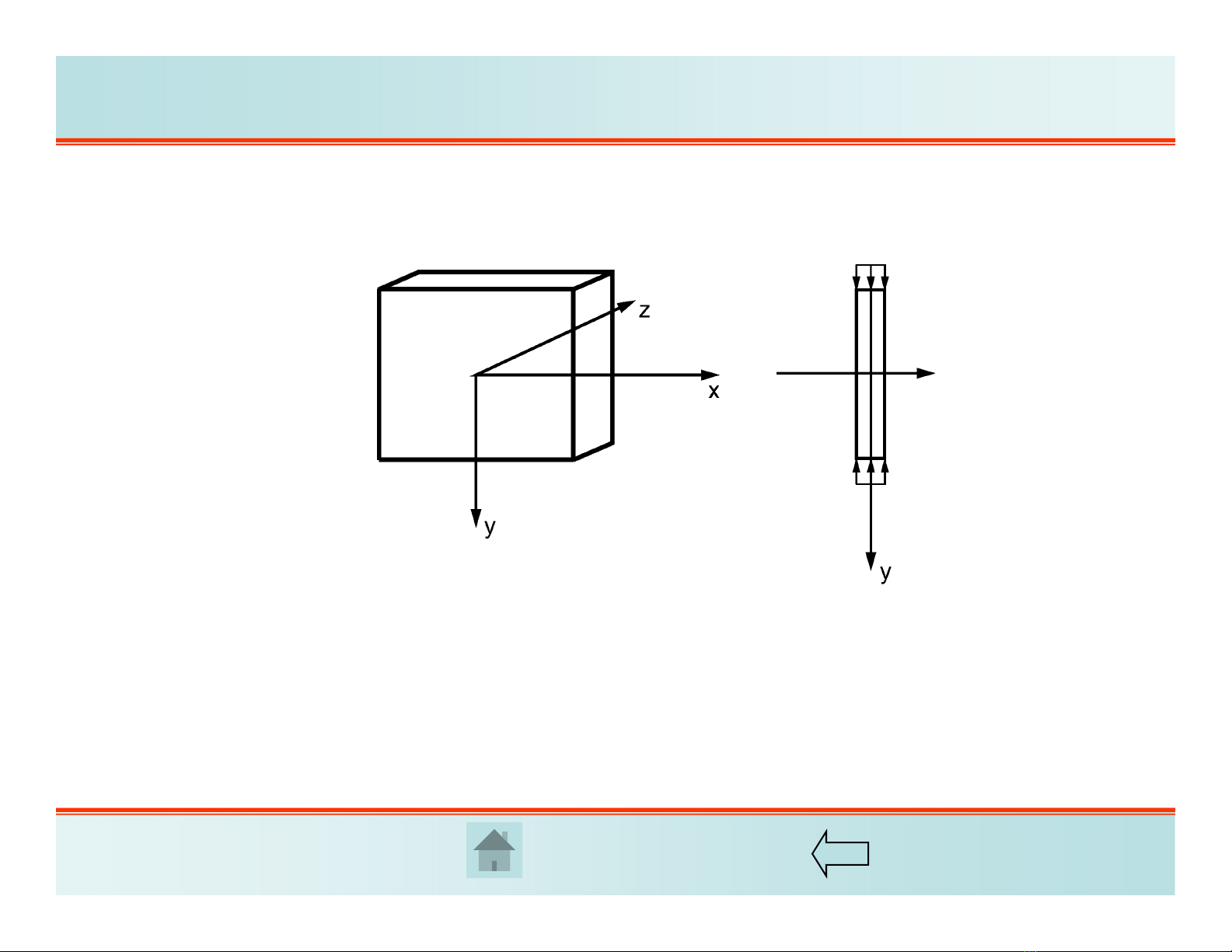
Khi vật thể có dạng tấm mỏng, tải trọng nằm trong mặt phẳng giữa tấm, phân bố đều
theo bề dày tấm thì có thể xem rằng:
a. Các ứng suất z=zx =zy =0
b. Các ứng suất trong mặt phẳng không đổi theo bề dày tấm, không phụ thuộc tọa độz
1. Ứng suất phẳng
5.1. KHÁI NIỆM BÀI TOÁN PHẲNG
08/01/2024 22:08 111
TS. Lương Văn Hải
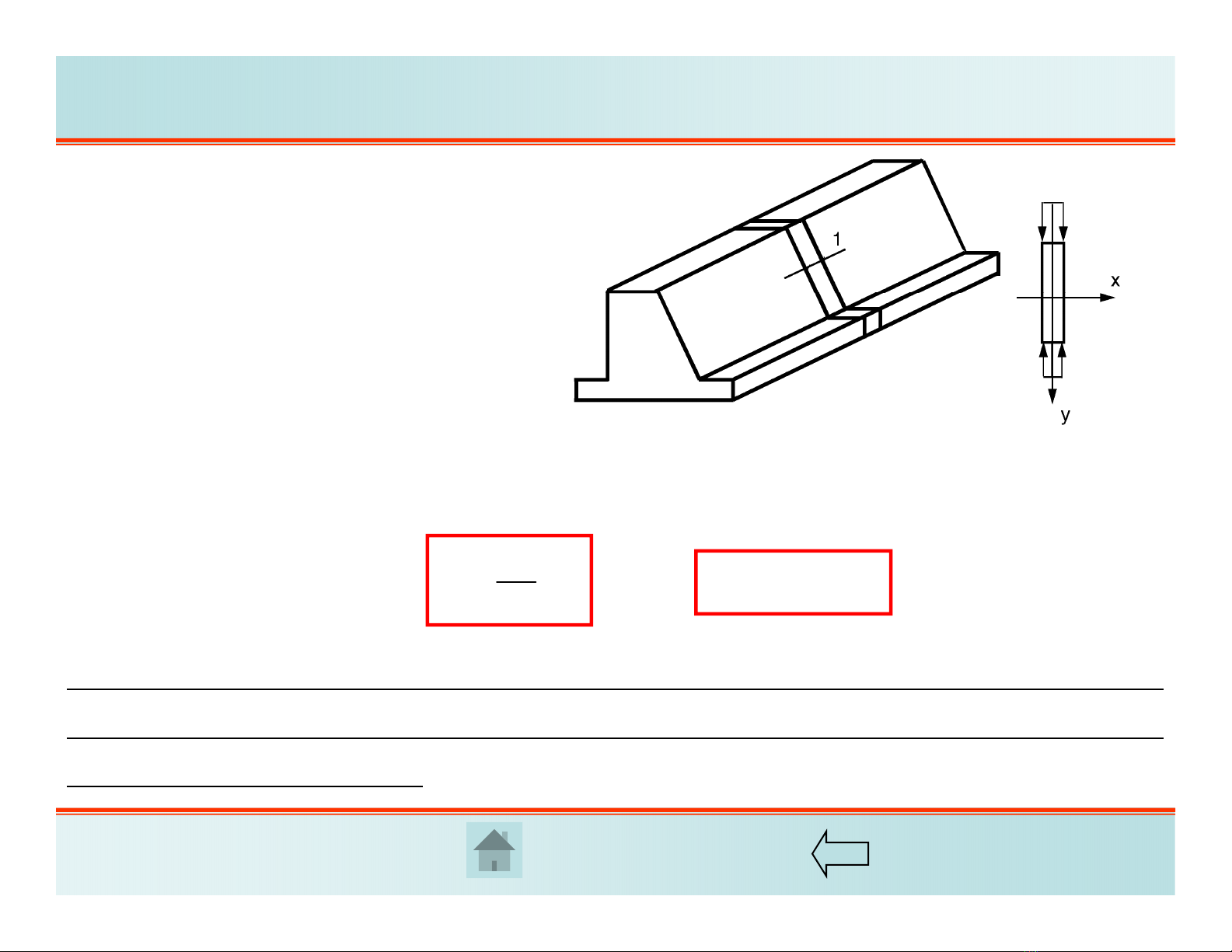
Khi bài toán có dạng lăng trụ dài và có mặt cắt ngang không đổi, chịu tải trọng
vuông góc với trục zvà phân bố đều dọc theo chiều dài thì ta có thể xem rằng w=0và
do đó suy ra:
2. Biến dạng phẳng
0
z
w
z
0
zx zy
Khi giải các bài toán phẳng, các phương trình cân bằng và biến dạng trong mặt phẳng
xy là giống nhau cho cả ứng suất phẳng và biến dạng phẳng. Chỉ có phương trình ứng
xử của vật liệu là khác nhau.
5.2. THIẾT LẬP PHƯƠNG TRÌNH CHỦ ĐẠO
08/01/2024 22:08 112
TS. Lương Văn Hải
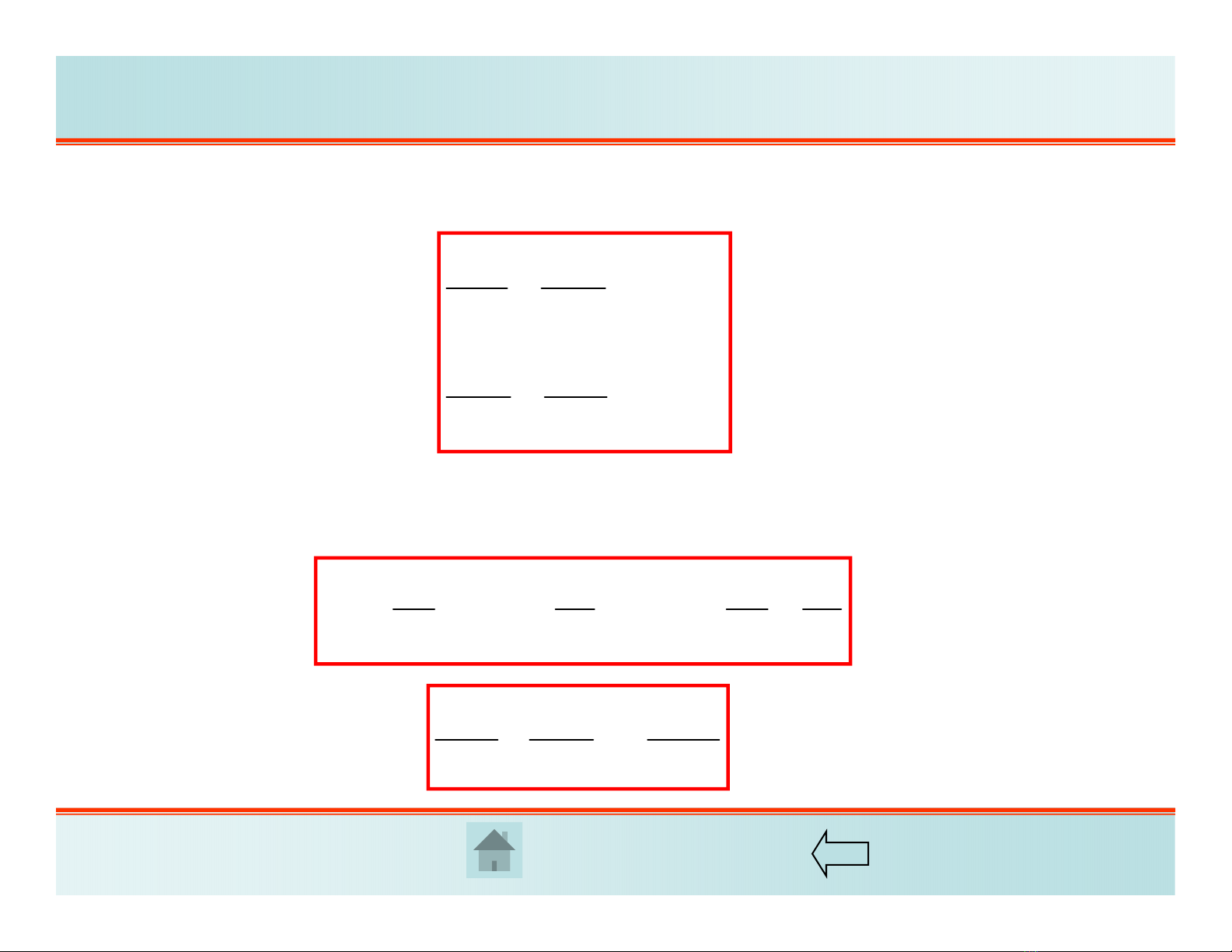
1. Phương trình cân bằng
0
0
xy
x
xy y
X
xy
Y
xy
2. Phương trình biến dạng
;;
xyxy
uv uv
x
yyx
Điều kiện tương thích 22
2
22
yxy
x
y
xx
y












![Bài giảng Quản lý vận hành và bảo trì công trình xây dựng [chuẩn nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20251006/agonars97/135x160/30881759736164.jpg)









![Ngân hàng câu hỏi trắc nghiệm Sức bền vật liệu 1: [Mô tả/Định tính Thêm để Tăng CTR]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250920/kimphuong1001/135x160/6851758357416.jpg)


![Trắc nghiệm Kinh tế xây dựng [chuẩn nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250920/kimphuong1001/135x160/32781758338877.jpg)
