08/01/2024 22:08 210
TS. Lương Văn Hải
CHƯƠNG 8. LÝ THUYẾT UỐN TẤM MỎNG
8.1. Khái niệm và giả thiết
8.2. Phương trình vi phân của tấm chịu uốn
8.3. Điều kiện biên
8.4. Tấm chữ nhật tựa đơn 4 cạnh – nghiệm Navier
8.5. Tấm chữ nhật tựa đơn 4 cạnh – nghiệm Lévy và Nádai
8.6. Bài toán đối xứng trục của tấm tròn
8.1. KHÁI NIỆM VÀ GIẢ THIẾT
08/01/2024 22:08 211
TS. Lương Văn Hải
Tấmlàvậtthểhìnhdạngphẳngcóbềdàyhnhỏsovớihaiphương
còn lại. Khi , thì tấm được coi là mỏng.
Nếu tấm có bề dày lớn hơn thì trở thành tấm dày, hoặc bài toán đàn
hồi không gian.
Mặt giữa là mặt phẳng chia đôi bề dày tấm và cũng còn gọi là mặt
trung bình.
Khái niệm mặt giữa đối với tấm tương tự như khái niệm trục thanh
trong SBVL.
1. Khái niệm
/1/5hl
8.1. KHÁI NIỆM VÀ GIẢ THIẾT
2. Giả thiết
Để giảm bớt sự phức tạp nhưng vẫn đảm bảo sự chính xác cần thiết,
giả thiết như sau:
1- Pháp tuyến thẳng và vuông góc với mặt giữa. Bỏ qua biến dạng
theo phương pháp tuyến, tức là coi . (Kirchoff).
2- Ứng suất pháp nhỏ so với các thành phần khác và có thể bỏ qua.
3- Mặt giữa không co giãn khi tấm chịu uốn. Giả thiết này tương tự
như trục thanh chịu uốn không co giãn trong SBVL.
4- Biến dạng và độ võng của tấm là bé.
0
z
z
08/01/2024 22:08 212
TS. Lương Văn Hải
8.2. PHƯƠNG TRÌNH VI PHÂN CỦA TẤM CHỊU UỐN
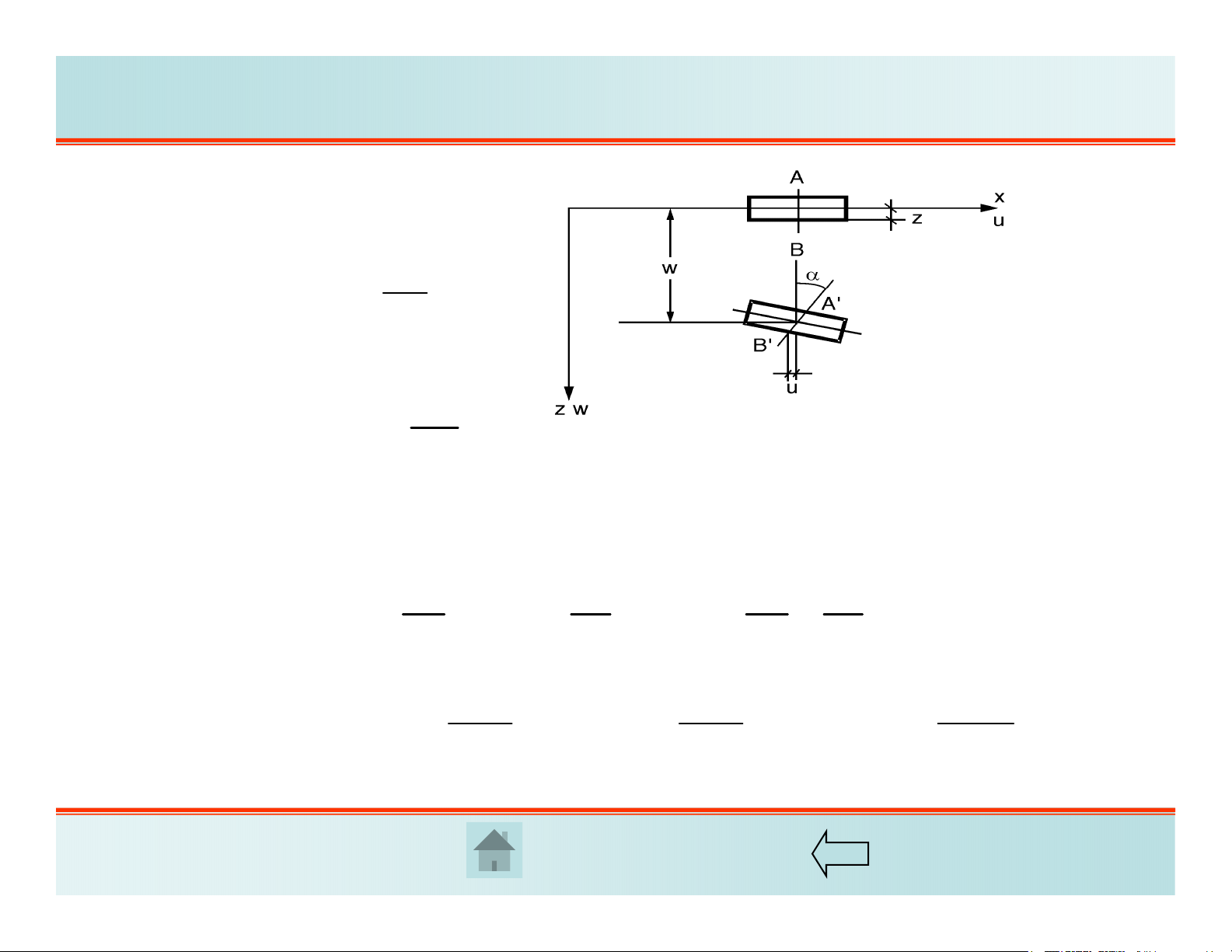
1. Phương trình hình học
Vì góc xoay α bé nên:
w
uz ztg z
x

  
Tương tự chuyển vị của B’
theo hướng y: w
vz
y

Các thành phần biến dạng theo Cauchy:
;;
xyxy
uv uv
x
yyx




22 2
22
;;2
xyxy
ww w
zz z
xy
x
y


  

08/01/2024 22:08 213
TS. Lương Văn Hải
8.2. PHƯƠNG TRÌNH VI PHÂN CỦA TẤM CHỊU UỐN
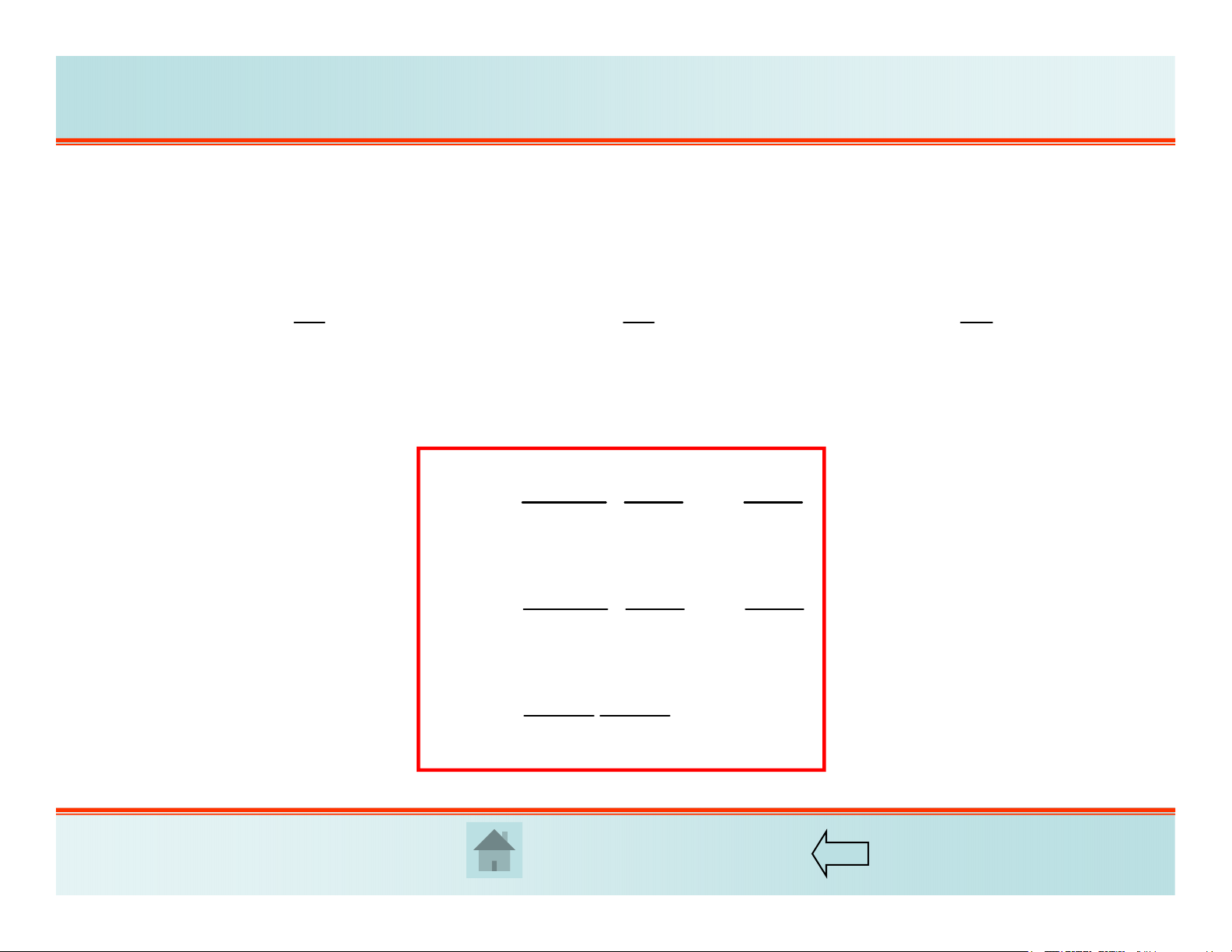
2. Phương trình vật liệu
Theo giả thiết 2, ta có . Định luật Hooke tổng quát trở thành:
Thế vào ta được:
11 1
(); ();
x
xy y yxxy xy
EE G


0
z
22
22 2
22
22 2
2
()
1
()
1
1
x
y
xy
E
zw w
x
y
E
zw w
yx
Ez w
xy








 
08/01/2024 22:08 214
TS. Lương Văn Hải