1
Chương 3. Khảo sát ổnđịnh hệtuyến tính liên tục.
Điều khiển tự động
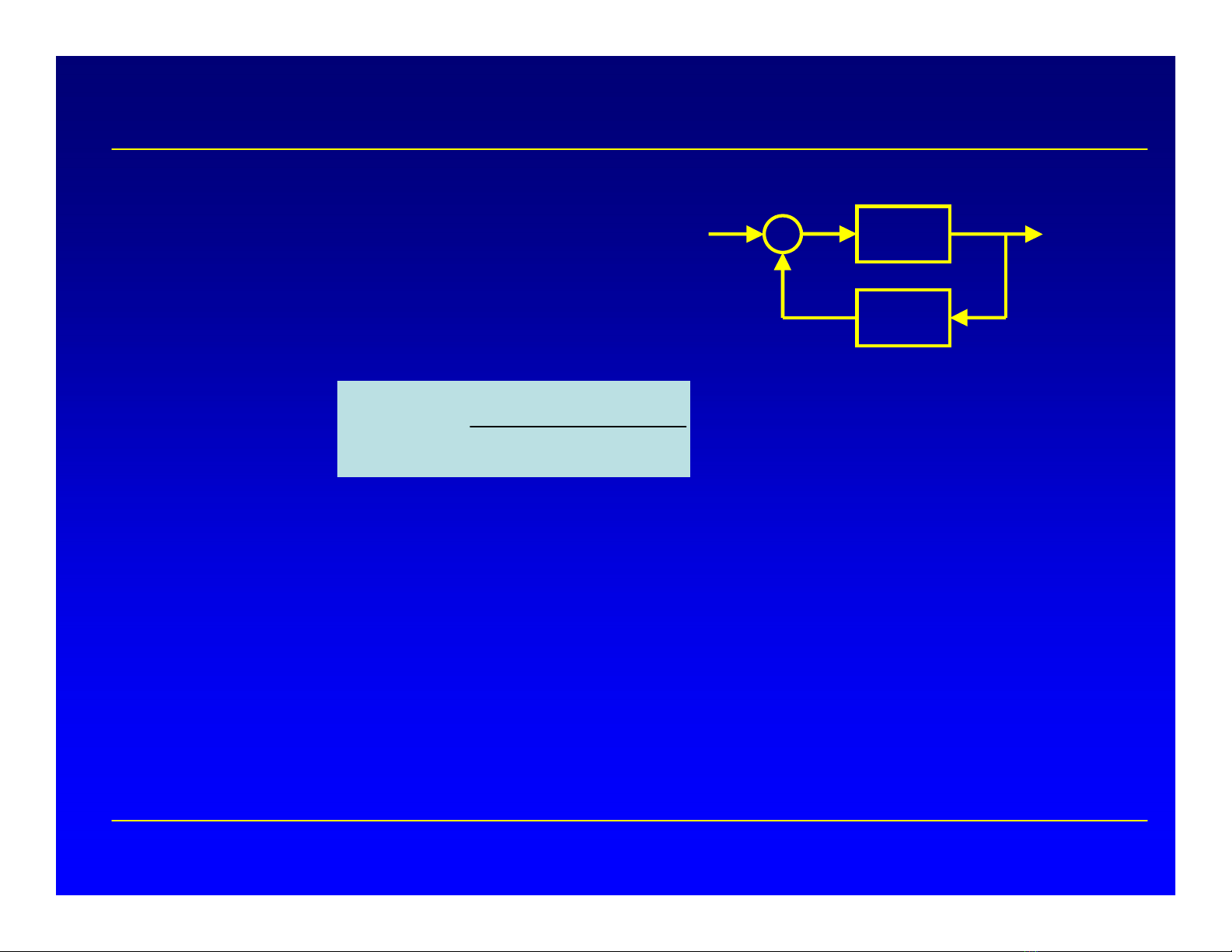
G
R
-
C
H
Cho hệthống:
Hàm truyền vòng kín:
)()(1
)
(
)( pHpG
p
G
pM
Phương trình đặctrưng (PTĐT):
F(p) = 1 + G(p).H(p) = 0
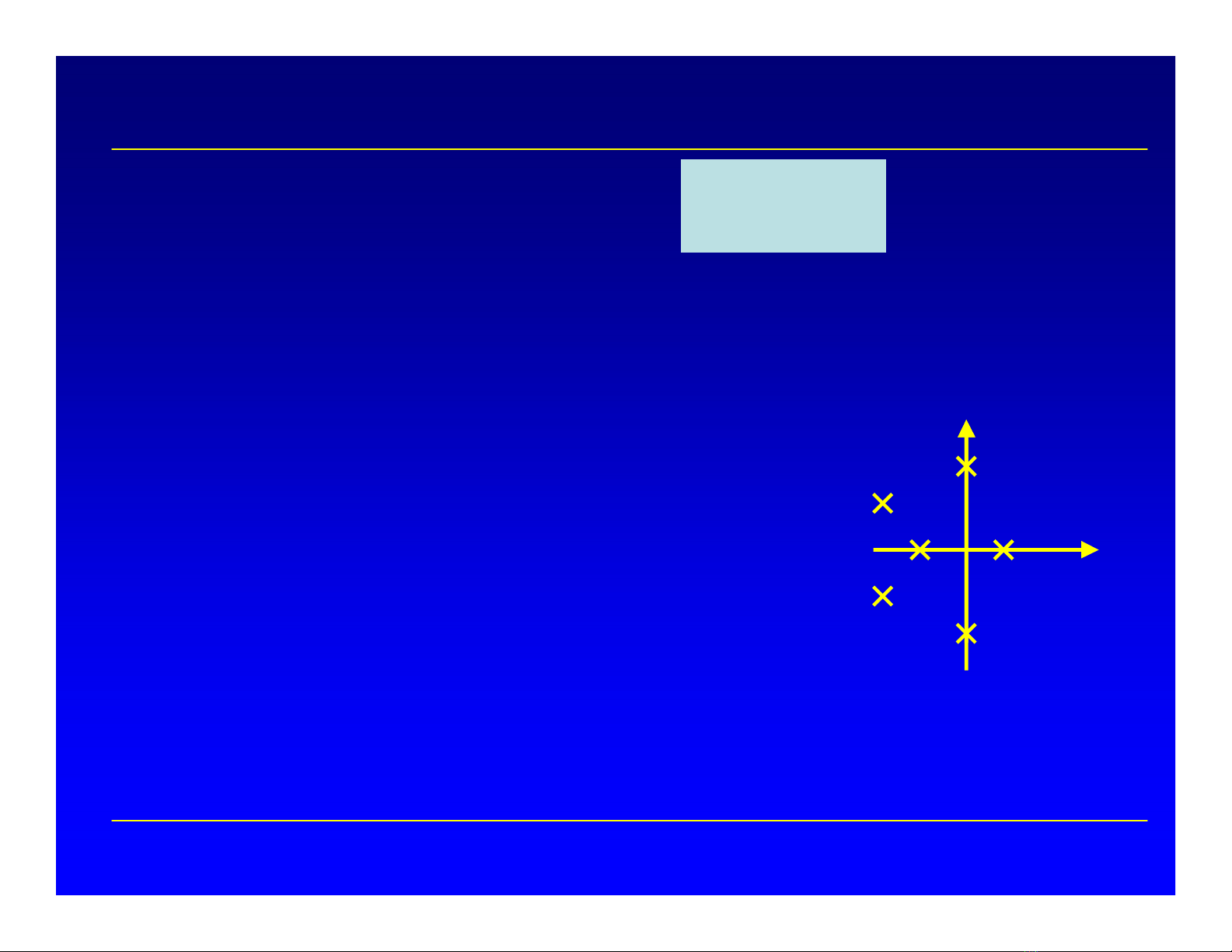
Định nghĩa hệthống ổnđịnh : tín hiệu ngõ ra bịchặn khi tín
hiệu ngõ vào bịchặn.
|r(t)| ≤N < ∞| c(t) | ≤M < ∞
I. Khái niệm chung
2
Chương 3. Khảo sát ổnđịnh hệtuyến tính liên tục.
Điều khiển tự động
+ Hệthống ổnđịnh khi các cực của M(p) có phần
thực âm hay nghiệm của PTĐT nằm bên trái mặt
phẳng phức (TMP)
+ Hệthống ởbiên giớiổnđịnh khi PTĐT có ít nhất
1 nghiệm nằm trên trụcảo, tất cảcác nghiệm còn
lại nằm bên trái mặt phẳng phức (TMP).
+ Hệthống không ổnđịnh khi PTĐT có ít nhất 1
nghiệm nằm bên phải mặt phẳng phức (PMP).
(ví dụvới Matlab)
Re
Im
Nghiệm của PTVP có dạng tổng quát:
n
i
tp
ii
etc
1
)(
Để c(t) bịchặn khi t ∞thì piphải có phần thực âm.
3
Chương 3. Khảo sát ổnđịnh hệtuyến tính liên tục.
Điều khiển tự động
II. Tiêu chuẩnổnđịnh đại số
Xét hệcó PTĐT như sau:
F(p) = anpn+ an-1 pn-1 +…+a0= 0 (an≠0).
Điều kiện cầnđể hệ ổnđịnh:
+ ajphải cùng dấu với an.
+ aj≠0 (không một hệsốajnào vắng mặt trong phương
trình đặc trưng).
1. Điều kiện cần
2. Tiêu chuẩnổnđịnh Routh
Điều kiện cần và đủ để các nghiệm của PTDT nằmởTMP (hệ ổn
định) là tất cảcác phần tửcủa cột 1 bảng Routh đều cùng dấu.
Nếu có sự đổi dấu thì sốlầnđổi dấu chính là sốnghiệm nằmởPMP.
4
Chương 3. Khảo sát ổnđịnh hệtuyến tính liên tục.
Điều khiển tự động
.........
.........
0
1
753
3
642
2
531
1
42
p
p
cccp
bbbp
aaap
aaap
nnn
n
nnn
n
nnn
n
nnn
n
Phương pháp thành lập bảng Routh:
1
321
2
nnnn
na
aaaa
b
1
541
4
n
nnnn
na
aaaa
b
2
1432
3
n
nnnn
nb
abab
c
PTĐT: F(p) = anpn+ an-1 pn-1 +…+a0= 0 (an≠0).
Trong đó:
5
Chương 3. Khảo sát ổnđịnh hệtuyến tính liên tục.
Điều khiển tự động
Các trường hợpđặc biệt:
Nếu có phần tử ở cột 1 bằng 0 thì thay 0 bằng εvà tính
giới hạn của phần tửtiếp theo của cột 1 khi ε0.
3
0 khi
66
bang 0 Thay30
62
331
0
1
2
3
4
p
p
p
p
p