intTypePromotion=1
zunia.vn Tuyển sinh 2024 dành cho Gen-Z zunia.vn zunia.vn
ADSENSE
 » 
 » 

Bài giảng Động lực học công trình: Chương 2 - GV. Trịnh Bá Thắng

Chia sẻ: _ _ | Ngày: | Loại File: PDF | Số trang:76

Thêm vào BST
Báo xấu
20
lượt xem 4
download
 
  Download Vui lòng tải xuống để xem tài liệu đầy đủ

Bài giảng "Động lực học công trình: Chương 2 - GV. Trịnh Bá Thắng" trình bày nội dung kiến thức về: Thiết lập hệ phương trình vi phân chuyển động; Dao động tự do; Phản ứng với tải trọng điều hòa; Phản ứng với tải trọng chu kỳ; Phản ứng với tải trọng xung. Mời các bạn cùng tham khảo bài giảng.

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Bài giảng Động lực học công trình: Chương 2 - GV. Trịnh Bá Thắng

  1. lOMoARcPSD|16911414 Chương 2: HỆ MỘT BẬC TỰ DO  Nội dung chƣơng 2 (12t): 1. Thiết lập hệ phương trình vi phân chuyển động 2. Dao động tự do 3. Phản ứng với tải trọng điều hòa 4. Phản ứng với tải trọng chu kỳ 5. Phản ứng với tải trọng xung 6. Bài tập chương 2. 19-Oct-21 GV Trịnh Bá Thắng 45 Downloaded by Nguynhavy Ha Vy (Ntkphuong205@gmail.com)
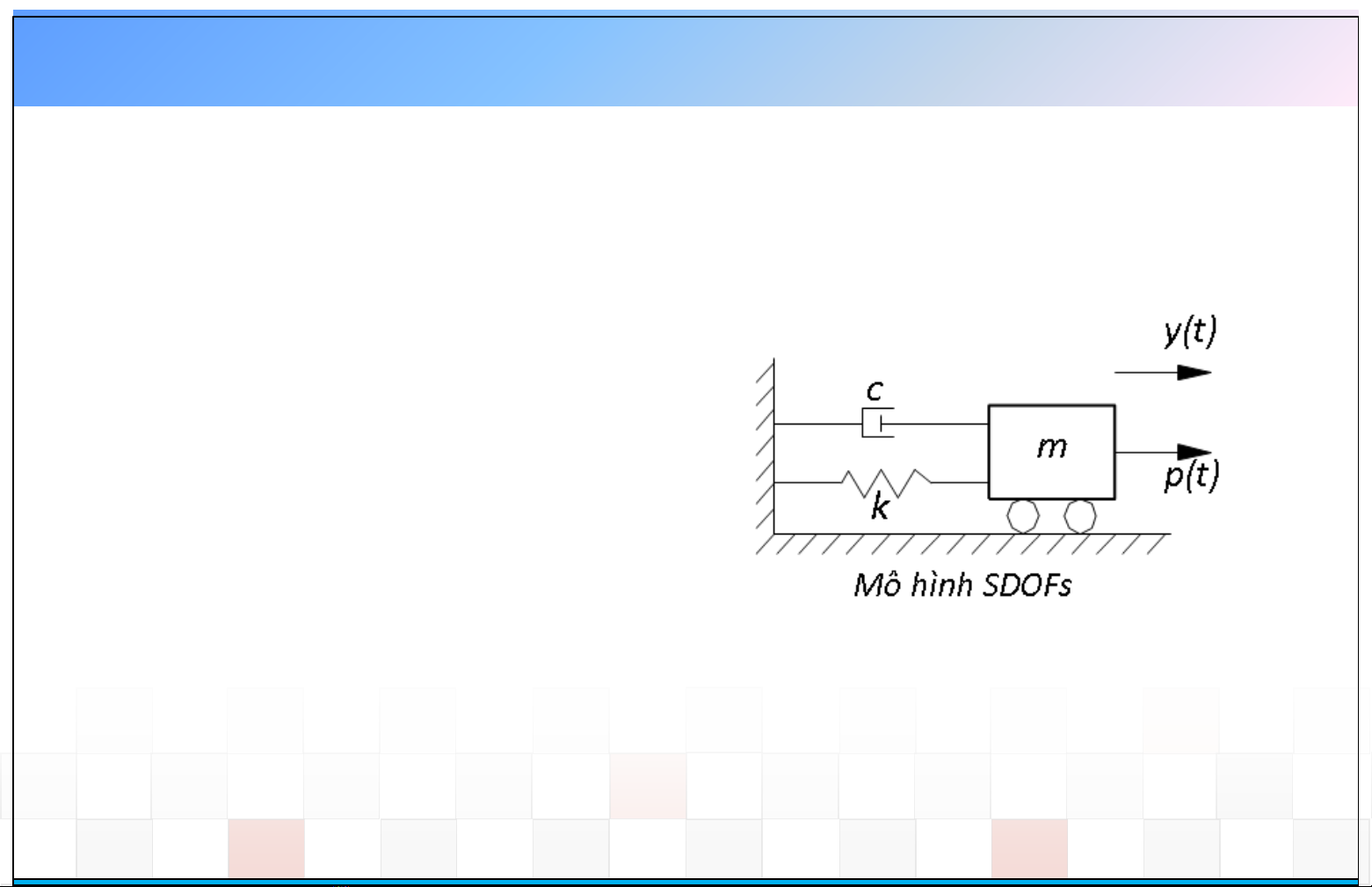
  2. lOMoARcPSD|16911414 Chương 2: HỆ MỘT BẬC TỰ DO I. THIẾT LẬP PHƢƠNG TRÌNH VI PHÂN CHUYỂN ĐỘNG 1. Mô hình hệ 1 BTD o Single Degree of Freedom system – SDOF  Khối lượng m  Độ cứng k  Hệ số cản c  Lực kích động p(t)  Vị trí khối lượng thời điểm y(t) = v(t) o Hệ một bậc tự do có các đặc trưng phân bố m, k, c, p(t) đều có thể đưa về mô hình có các đặc trưng vật lý tập trung (hệ một bậc tự do suy rộng) 19-Oct-21 GV Trịnh Bá Thắng 46 Downloaded by Nguynhavy Ha Vy (Ntkphuong205@gmail.com)
  3. lOMoARcPSD|16911414 Chương 2: HỆ MỘT BẬC TỰ DO I. THIẾT LẬP PHƢƠNG TRÌNH VI PHÂN CHUYỂN ĐỘNG 2. Thiết lập phƣơng trình vi phân chuyển động  Nguyên lý D’Alambert p(t) + fS + fI + fD =0 Hay (2.1)  Nguyên lý công khả dĩ o Cho khối lượng chuyển vị khả dĩ v. Công khả dĩ: W = p(t)v + fS v + fI v + fD v = 0 hay o Vì v  0 nên thu được giống như (2.1) 19-Oct-21 GV Trịnh Bá Thắng 47 Downloaded by Nguynhavy Ha Vy (Ntkphuong205@gmail.com)
  4. lOMoARcPSD|16911414 Chương 2: HỆ MỘT BẬC TỰ DO I. THIẾT LẬP PHƢƠNG TRÌNH VI PHÂN CHUYỂN ĐỘNG 2. Thiết lập phƣơng trình vi phân chuyển động  Nguyên lý Hamilton o Động năng của hệ: → Biến phân động năng: o Thế năng biến dạng đàn hồi của lò xo: → Biến phân: o Biến phân công của lực không bảo toàn p(t) và fD (tức là công khả dĩ của hai lực này trên chuyển vị khả dĩ v): o Theo nguyên lý Hamilton 19-Oct-21 GV Trịnh Bá Thắng 48 Downloaded by Nguynhavy Ha Vy (Ntkphuong205@gmail.com)
  5. lOMoARcPSD|16911414 Chương 2: HỆ MỘT BẬC TỰ DO I. THIẾT LẬP PHƢƠNG TRÌNH VI PHÂN CHUYỂN ĐỘNG 2. Thiết lập phƣơng trình vi phân chuyển động  Nguyên lý Hamilton 𝑡2 𝑚. 𝑣 𝛿𝑣 − 𝑘. 𝑣. 𝛿𝑣 − 𝑐. 𝑣 𝛿𝑣 + 𝑝 𝑡 . 𝛿𝑣 𝑑𝑡 = 0 (2.2) 𝑡1 o Tích phân từng số hạng thứ nhất (2.3) o Thế (2.3) vào (2.2): (2.4) 19-Oct-21 GV Trịnh Bá Thắng 49 Downloaded by Nguynhavy Ha Vy (Ntkphuong205@gmail.com)
  6. lOMoARcPSD|16911414 Chương 2: HỆ MỘT BẬC TỰ DO I. THIẾT LẬP PHƢƠNG TRÌNH VI PHÂN CHUYỂN ĐỘNG 2. Thiết lập phƣơng trình vi phân chuyển động  Kết quả: Cả 3 phương pháp cho cùng kết quả: o Đây là phương trình vi phân chuyển động tổng quát hệ 1 BTD o Dựa vào p(t): Dao động tự do, dao động điều hòa, dao động có chu kỳ, dao động xung, dao động tổng quát,… o Trọng lượng không ảnh hưởng đến phương trình vi phân chuyển động. o Sự rung động tại mặt đất tương tự như đặt lực kích động Peff tại vị trí khối lượng. 19-Oct-21 GV Trịnh Bá Thắng 50 Downloaded by Nguynhavy Ha Vy (Ntkphuong205@gmail.com)
  7. lOMoARcPSD|16911414 Chương 2: HỆ MỘT BẬC TỰ DO II. DAO ĐỘNG TỰ DO 1. Một số định nghĩa o Chu kỳ dao động (T): là thời gian cần thiết để thực hiện một dao 2П động toàn phần. T = (s) ω o Tần số dao động (f): Là số lần dao động trong một giây 1 ω f= = (1/s) T 2П o Tần số góc (tần số dao động riêng) w: Là số lần dao động trong 2p giây 2П ω= = 2П. f (rad/s) T 19-Oct-21 GV Trịnh Bá Thắng 51 Downloaded by Nguynhavy Ha Vy (Ntkphuong205@gmail.com)
  8. lOMoARcPSD|16911414 Chương 2: HỆ MỘT BẬC TỰ DO II. DAO ĐỘNG TỰ DO 1. Một số khái niệm  Bậc tự do là chuyển vị thẳng: k 1 ω= = m m.δ11 • k: Độ cứng đàn hồi của hệ, là lực (vị trí khối lượng) gây ra chuyển vị thẳng bằng 1 (tại vị trí khối lượng). • m: Khối lượng tập trung của hệ. • 11: Độ mềm đàn hồi của hệ, là chuyển vị thẳng (tại vị trí khối lượng) do lực bằng 1 ( vị trí khối lượng) gây ra. 1 δ11 = . (M1 )(M1 ) EI 19-Oct-21 GV Trịnh Bá Thắng 52 Downloaded by Nguynhavy Ha Vy (Ntkphuong205@gmail.com)
  9. lOMoARcPSD|16911414 Chương 2: HỆ MỘT BẬC TỰ DO II. DAO ĐỘNG TỰ DO 1. Một số khái niệm  Nếu bậc tự do là chuyển vị xoay: 𝑘 1 ω= = 𝐼𝑚 𝐼𝑚.δ11 • k: Độ cứng đàn hồi của hệ, là mômen (vị trí tâm quay) gây ra chuyển vị xoay bằng 1 (tại vị trí tâm quay). • Im: Mô men quán tính khối lượng lấy với tâm quay. Im = mi . L2i • 11: Độ mềm đàn hồi của hệ, là chuyển vị xoay (tại vị trí tâm quay) do mô men bằng 1 ( vị trí tâm quay) gây ra. 19-Oct-21 GV Trịnh Bá Thắng 53 Downloaded by Nguynhavy Ha Vy (Ntkphuong205@gmail.com)
  10. lOMoARcPSD|16911414 Chương 2: HỆ MỘT BẬC TỰ DO II. DAO ĐỘNG TỰ DO 2. Phƣơng trình vi phân dao động tự do o Phương trình vi phân dao động tự do có dạng: ( p(t) = 0 ) m. v + c. v + k. v = 0 o Thông số ban đầu: chuyển vị ban đầu v(0), vận tốc ban đầu v(0) 𝑣 (0) 𝑣(0) o Hệ số cản: c = 0, dao động không cản. o Hệ số cản: c ≠ 0, dao động có cản. 19-Oct-21 GV Trịnh Bá Thắng 54 Downloaded by Nguynhavy Ha Vy (Ntkphuong205@gmail.com)
  11. lOMoARcPSD|16911414 Chương 2: HỆ MỘT BẬC TỰ DO II. DAO ĐỘNG TỰ DO 3. Dao động tự do không cản (c = 0) o Phương trình vi phân dao động tự do không cản có dạng: k m. v + k. v = 0 đặt w  2 m o Nghiệm của phương trình có dạng: v(t) = A.sin wt + B.cos wt với → v(t)= A.w.cos wt – B.w.sin wt → B = v(0); A.w = v(0) 𝑣 (0) v(t) = . sin ωt + v(0). cos ωt ω Hoặc v(t) = ρ. cos (ωt - θ) 19-Oct-21 GV Trịnh Bá Thắng 55 Downloaded by Nguynhavy Ha Vy (Ntkphuong205@gmail.com)
  12. lOMoARcPSD|16911414 Chương 2: HỆ MỘT BẬC TỰ DO II. DAO ĐỘNG TỰ DO 3. Dao động tự do không cản (c = 0) o Hệ chỉ chịu chuyển vị ban đầu: v(0) ≠ 0; v(0)= 0 v(t) = v(0). cos ωt П ω 𝟐П ω 19-Oct-21 GV Trịnh Bá Thắng 56 Downloaded by Nguynhavy Ha Vy (Ntkphuong205@gmail.com)
  13. lOMoARcPSD|16911414 Chương 2: HỆ MỘT BẬC TỰ DO II. DAO ĐỘNG TỰ DO 3. Dao động tự do không cản (c = 0) o Hệ chỉ chịu vận tốc ban đầu: v(0) = 0; v(0) ≠ 0 v(0) v(t) = . sin ωt ω 𝟑П v(0) 𝟐ω ω v(0) П 𝟐П ω 𝟐ω ω 19-Oct-21 GV Trịnh Bá Thắng 57 Downloaded by Nguynhavy Ha Vy (Ntkphuong205@gmail.com)
  14. lOMoARcPSD|16911414 Chương 2: HỆ MỘT BẬC TỰ DO II. DAO ĐỘNG TỰ DO 3. Dao động tự do không cản (c = 0) o Hệ chịu kích thích ban đầu v(0) ≠ 0; v(0) ≠ 0 v(0) v(t) = . sin ωt + v(0). cos ωt ω v(o) 19-Oct-21 GV Trịnh Bá Thắng 58 Downloaded by Nguynhavy Ha Vy (Ntkphuong205@gmail.com)
  15. lOMoARcPSD|16911414 Chương 2: HỆ MỘT BẬC TỰ DO II. DAO ĐỘNG TỰ DO 3. Dao động tự do không cản (c = 0) o Trường hợp xét đến trọng lượng bản thân G, v(0) ≠ 0; v 0 = 0 G v(t) = ρ. cos (ωt - θ) + vt với vt = = G. δ11 k 19-Oct-21 GV Trịnh Bá Thắng 59 Downloaded by Nguynhavy Ha Vy (Ntkphuong205@gmail.com)
  16. lOMoARcPSD|16911414 Chương 2: HỆ MỘT BẬC TỰ DO II. DAO ĐỘNG TỰ DO 3. Dao động tự do không cản (c = 0)  Ví dụ 2.1: Hệ 1 BTD như hình vẽ 1. Xác định tần số dao động riêng của hệ. 2. Vẽ đồ thị dao động của khối lượng m với các trạng thái kích thích ban đầu khác nhau (bỏ qua lực cản). 19-Oct-21 GV Trịnh Bá Thắng 60 Downloaded by Nguynhavy Ha Vy (Ntkphuong205@gmail.com)
  17. lOMoARcPSD|16911414 Chương 2: HỆ MỘT BẬC TỰ DO  Xác định theo độ cứng o Độ cứng của dầm: 48EI 6EI k= = 2L 3 L3 o Tần số dao động riêng: k 6EI ω= = m m.L3 19-Oct-21 GV Trịnh Bá Thắng 61 Downloaded by Nguynhavy Ha Vy (Ntkphuong205@gmail.com)
  18. lOMoARcPSD|16911414 Chương 2: HỆ MỘT BẬC TỰ DO  Xác định theo độ mềm o Biểu đồ (M1) như hình vẽ 1 1 1 L 2L L3 δ11 = M1 M1 = L. . . 2 = EI EI 2 2 3 2 6EI o Tần số dao động riêng: 1 6EI ω= = m.δ11 m.L3 19-Oct-21 GV Trịnh Bá Thắng 62 Downloaded by Nguynhavy Ha Vy (Ntkphuong205@gmail.com)
  19. lOMoARcPSD|16911414 Chương 2: HỆ MỘT BẬC TỰ DO  Xét trường hợp chuyển vị ban đầu: v(0) ≠ 0; v(0)= 0 П ω 𝟐П ω 19-Oct-21 GV Trịnh Bá Thắng 63 Downloaded by Nguynhavy Ha Vy (Ntkphuong205@gmail.com)
  20. lOMoARcPSD|16911414 Chương 2: HỆ MỘT BẬC TỰ DO II. DAO ĐỘNG TỰ DO 3. Dao động tự do không cản (c = 0)  Ví dụ 2.2: Hệ 1 BTD như hình vẽ 1. Xác định tần số dao động riêng.(a =1m, M =100 kg, E =2.104 kN/cm2, I=2000cm4 ) 2. Xác định vị trí và vận tốc của hệ ở t = 1s. Biết tại thời điểm t =0 s, M chuyển vị 1cm, không tốc độ, bỏ qua lực cản. 19-Oct-21 GV Trịnh Bá Thắng 64 Downloaded by Nguynhavy Ha Vy (Ntkphuong205@gmail.com)
ADSENSE

CÓ THỂ BẠN MUỐN DOWNLOAD

LV.15: Bộ Đồ Án Tốt Nghiệp Chuyên Ngành Cơ Khí
65 tài liệu
2431 lượt tải
THÔNG TIN
TRỢ GIÚP
HỖ TRỢ KHÁCH HÀNG
Theo dõi chúng tôi

Chịu trách nhiệm nội dung:

Nguyễn Công Hà - Giám đốc Công ty TNHH TÀI LIỆU TRỰC TUYẾN VI NA

LIÊN HỆ

Địa chỉ: P402, 54A Nơ Trang Long, Phường 14, Q.Bình Thạnh, TP.HCM

Hotline: 093 303 0098

Email: support@tailieu.vn

Giấy phép Mạng Xã Hội số: 670/GP-BTTTT cấp ngày 30/11/2015 Copyright © 2022-2032 TaiLieu.VN. All rights reserved.

 

Đồng bộ tài khoản
2=>2