BÀI 10 ĐÁP NG T N S VÀ PH N H IỨ Ầ Ố Ả Ồ
BÀI 10 ĐÁP NG T N S VÀ PH N H I Ứ Ầ Ố Ả Ồ
10.1 Đáp ng t n s khu ch điứ ầ ố ế ạ
10.2 Khu ch đi đi n áp – ph n h i n i ti p – s nế ạ ệ ả ồ ố ế ơ
10.3 Khu ch đi đi n tr truy n đt – ph n h i s n –ế ạ ệ ở ề ạ ả ồ ơ
s nơ
10.4 Khu ch đi dòng – ph n h i s n – n i ti pế ạ ả ồ ơ ố ế
10.5 Khu ch đi đi n d n truy n đt – ph n h i n i ế ạ ệ ẫ ề ạ ả ồ ố
ti p – n i ti pế ố ế
BÀI GI NG K THU T ĐI N TẢ Ỹ Ậ Ệ Ử 1
BÀI 10 ĐÁP NG T N S VÀ PH N H IỨ Ầ Ố Ả Ồ
BÀI 10 ĐÁP NG T N S VÀ PH N H IỨ Ầ Ố Ả Ồ
10.1 Đáp ng t n s c a b khu ch điứ ầ ố ủ ộ ế ạ
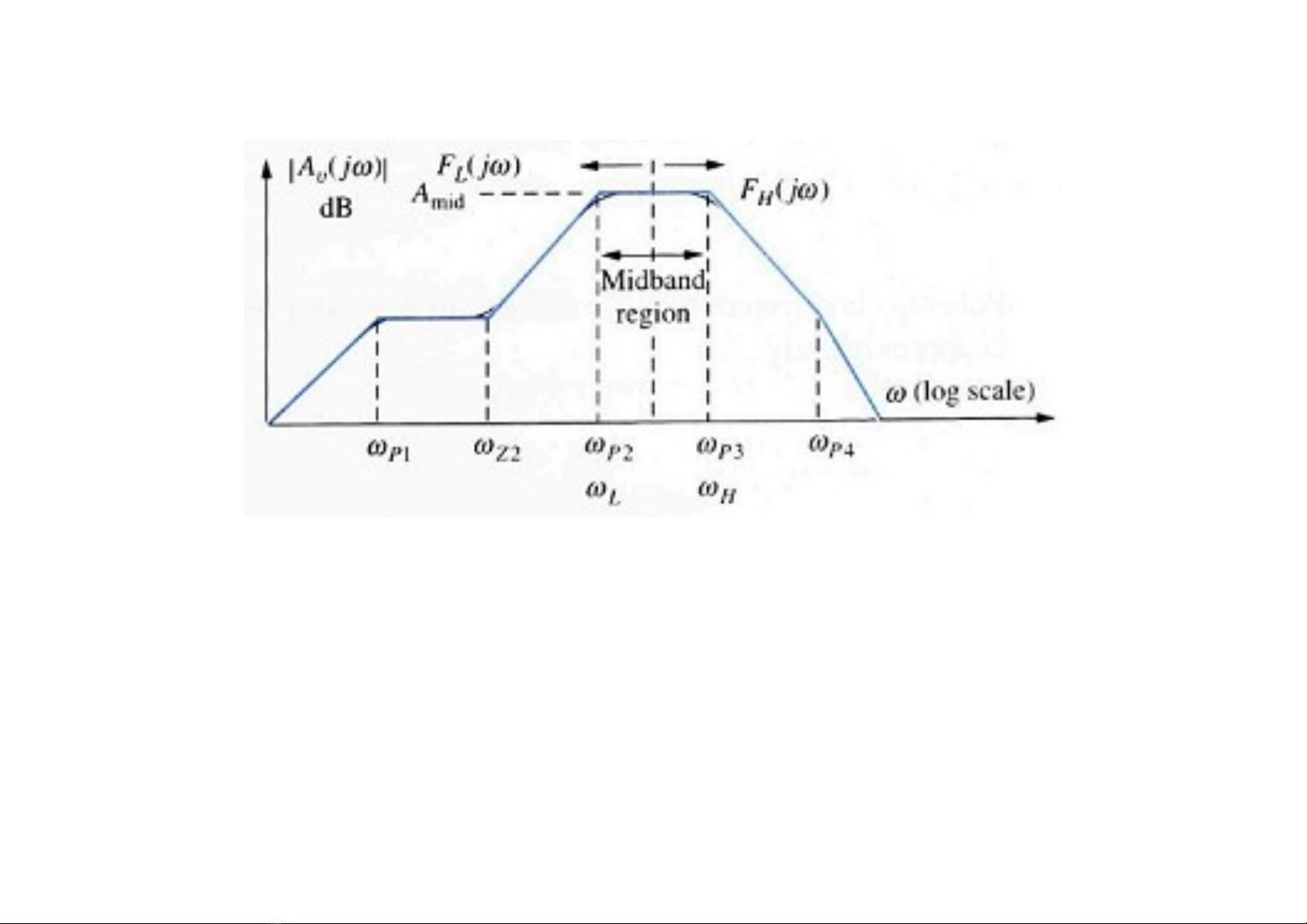
Hình 10.1.1 là đ th Bode cho biên đ c a h sồ ị ộ ủ ệ ố
khu ch đi đi n áp c a m t khu ch đi lý thuy t. Khôngế ạ ệ ủ ộ ế ạ ế
k đn các đi m c c và đi m không, hàm truy n đt đi nể ế ể ự ể ề ạ ệ
áp Av(s) có th đc vi t b ng t s c a hai đa th c theo ể ượ ế ằ ỷ ố ủ ứ s:
n
n
m
m
v
sbsbsbb
sasasaa
sD
sN
sA
...
...
2
210
2
210
(10.1.1)
BÀI GI NG K THU T ĐI N TẢ Ỹ Ậ Ệ Ử 2
BÀI 10 ĐÁP NG T N S VÀ PH N H IỨ Ầ Ố Ả Ồ
Có th k t h p thành hàm ể ế ợ FL(s) và các đi m cùng v iể ớ
đáp ng t n s cao trên vùng trung t n có th đc nhómứ ầ ố ầ ể ượ
thành hàm FH(s). Dùng FL và FL, Av(s) có th đc vi t l iể ượ ế ạ
là:
Av(s) = AmidFL(s)FH(s) (10.1.2)
BÀI GI NG K THU T ĐI N TẢ Ỹ Ậ Ệ Ử 3
BÀI 10 ĐÁP NG T N S VÀ PH N H IỨ Ầ Ố Ả Ồ
Hình 10.1.1 Đ th Bode cho hàm truy n đt khu ch điồ ị ề ạ ế ạ
t ng quátổ
BÀI GI NG K THU T ĐI N TẢ Ỹ Ậ Ệ Ử 4
BÀI 10 ĐÁP NG T N S VÀ PH N H IỨ Ầ Ố Ả Ồ
Trong đó Amid là h s khu ch đi trung t nệ ố ế ạ ầ trong
vùng gi a ữcác t n s c t trênầ ố ắ và d iướ (ωL và ωH t ngươ
ng). V i ứ ớ Amid rõ ràng trong ph ng trình ươ 10.1.2, FL(s) và
FH(s) ph i đc vi t thành hai d ng chu n đc bi t đcả ượ ế ạ ẩ ặ ệ ượ
xác đnh trong các ph ng trình ị ươ 10.1.3 và 10.1.4:
L
Pk
L
P
L
P
L
Zk
L
Z
L
Z
L
sss
sss
sF
...
...
21
21
(10.1.3)
BÀI GI NG K THU T ĐI N TẢ Ỹ Ậ Ệ Ử 5