1
1/22/20 1
Chương 2
KHÁI NIỆM
I. KHÁI QUÁT VỀ KHÁI NIỆM
II. CÁC THAO TÁC LOGIC ĐỐI VỚI KHÁI NIỆM
CHƯƠNG 2-KHÁI NIỆM
2
1/22/20
I. KHÁI QUÁT VỀ KHÁI NIỆM
I.1. Khái niệm là gì?
I.2. Nội hàm và Ngoại diên của khái niệm
I.3. Phân loại khái niệm
I.4. Quan hệ giữa các khái niệm
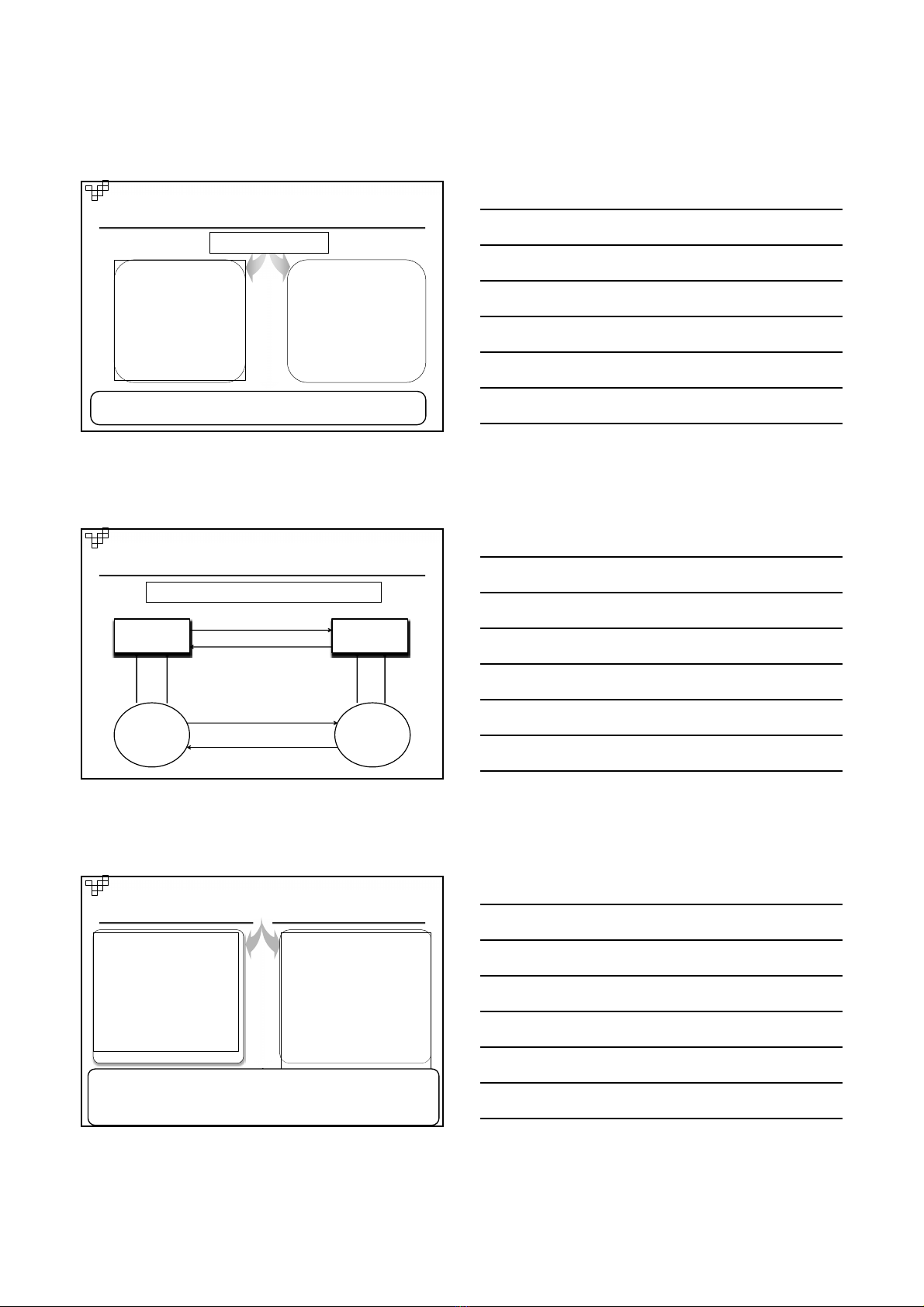
Sự hình thành khái niệm
Trìu
t
ượ
ng hóa
các DH
So sánh
các d
ấ
u
hi
ệ
u
Đ
T
Phân tích
đố
i t
ượ
ng
Đố
i
t
ượ
ng
T
ổ
ng h
ợ
p
các DH b
ả
n
ch
ấ
t
Khái quát
hóa các DH
b
ả
nch
ấ
t
Ngôn ng
ữ
hóa KN
Khái niệm là hình thức tư duy phản ánh những
dấu hiệu bản chất của đối tượng tư tưởng
I.1. Khái niệm là gì?
2
ØKhái niệm
•Có nội hàm & ngọai
diên, thể hiện hiểu biết
ổn định của loài người.
•Phụ thuộc vào quy
luật logic (giống nhau
ở mọi người, mọi dân
tộc, mọi thời đại).
ØTừ
•Có ký (tín) hiệu mang
nghĩa có thể thay đổi
theo người sử dụng.
•Phụ thuộc vào quy tắc
ngữ pháp (khác nhau
ởnhững người dùng
ngôn ngữ khác nhau).
Chỉ có nghĩa ổn định của từ mới đồng nhất với khái niệm.
Thuật ngữ là từ diễn đạt duy nhất một khái niệm.
Khái niệm & Từ
I.1. Khái niệm là gì?
Mối quan hệ giữa Khái niệm & Từ
Tư duy Ngôn ngữ
Khái
niệm Từ
Nội dung, quyết định
Phạm
trù
Nội dung, quyết định
Hình thức –Vỏ vật chất
Hình thức –Vỏ vật chất
I.1. Khái niệm là gì?
Hình
thức
ØNội hàm
•Là toàn thể các dấu
hiệu bản chất của đối
tượng tư tưởng mà khái
niệm phản ánh
•Có từ 1đến vài dấu hiệu
•Mang tính trừu tượng
•Chất của khái niệm
ØNgoại diên
•Là toàn thể các phần tử
có cùng dấu hiệu bản chất
hợp thành đối tượng tư
tưởng mà KN bao quát.
•Chứa từ 0đến vô số
phần tử.
•Mang tính khái quát.
•Lượng của khái niệm
I.2. Nội hàm và ngoại diên của khái niệm
•Nội hàm càng cạn thì ngoại diên càng rộng,nội hàm càng
sâu thì ngoại diên càng hẹp;
•Ngoại diên càng rộng thì nội hàm càng cạn,ngoại diên
càng hẹp thì nôi hàm càng sâu.
3
Dựa
vào
•KN quan hệ & KN không quan hệ
•KN khẳng định & KN phủ định
•KN cụ thể & KN trìu tượng
Khái niệm
KN thực KN ảo (rỗng)
KN riêng (đồng nhất)KN chung
KN vô hạn KN hữu hạn
Ngoại diên
Nội hàm
I.3. Phân loại khái niệm
QH đồng nhất
QH giao nhau
QH lệ thuộc
QH ngang hàng
QH đối chọi
QH mâu thuẫn
Không chung ph.tử ND
Có chung ph.tử ND
I.4. Quan hệ giữa các khái niệm
•Điều kiện cần & đủ để cho các khái niệm có quan hệ với nhau là
chúng phải có chung ít nhất một dấu hiệu nội hàm.
•Căn cứ vào ngoại diên có phần tử chung hay không mà những
KN có quan hệ với nhau được chia thành 2 nhóm gồm 6 quan hệ:
Những KN
có QH với
nhau
a) Ngoại diên có chung phần tử
A, B
A,B đồng nhất A lệ thuộc B
B
A
A,B giao nhau
A B
I.4. Quan hệ giữa các KN
Biểu diễn
QH giữa các
KH bằng sơ
đồ Venn
∃𝒙 𝒙 ∈ 𝑨 ∧ 𝒙 ∈ B;
∃𝒙 𝒙 ∈ 𝑨 ∧ 𝒙 ∉ B;
∃𝒙 𝒙 ∈ B ∧ 𝒙 ∉ A
∀𝒙 𝒙 ∈ 𝑨 → 𝒙 ∈ B;
∀𝒙 𝒙 ∈ 𝑩 → 𝒙 ∈ A;
∃𝒙 𝒙 ∈ 𝑨 ∧ 𝒙 ∈ B;
∃𝒙 𝒙 ∈ 𝑩 ∧ 𝒙 ∉ A;
4
A,B mâu thuẫn
AB
A,B ngang hàng
AB
A,B đối chọi
AB
b) Ngoại diên không có chung phần tử
I.4. Quan hệ giữa các KN
Biểu diễn
QH giữa các
KH bằng sơ
đồ Venn
CC
∀𝒙 𝒙 ∈ 𝑨 → 𝒙 ∈ 𝑪;
∀𝒙 x∈ 𝑩 → 𝒙 ∈ 𝑪;
∀𝒙 x∈ 𝑨 → 𝒙 ∉ 𝑩;
∀𝒙 x∈ 𝑩 → 𝒙 ∉ 𝑨;
∃𝒙 𝒙 ∈ 𝑪 ∧ 𝒙 ∉ 𝑩 ∧ 𝒙 ∉ 𝑨
∀𝒙 𝒙 ∈ 𝑨 → 𝒙 ∈ 𝑪;
∀𝒙 x∈ 𝑩 → 𝒙 ∈ 𝑪;
∀𝒙 x∈ 𝑨 → 𝒙 ∉ 𝑩;
∀𝒙 x∈ 𝑩 → 𝒙 ∉ 𝑨;
∃𝒙 𝒙 ∈ 𝑪 ∧ 𝒙 ∉ 𝑩 ∨ 𝑨
∀𝒙 𝒙 ∈ 𝑨 → 𝒙 ∈ 𝑪;
∀𝒙 x∈ 𝑩 → 𝒙 ∈ 𝑪;
∀𝒙 x∈ 𝑨 → 𝒙 ∉ 𝑩;
∀𝒙 x∈ 𝑩 → 𝒙 ∉ 𝑨;
∃𝒙 𝒙 ∈ 𝑪 ∧ 𝒙 ∉ 𝑩 ∧ 𝑨
Ví dụ minh hoạ:Dùng biểu đồ Venn, hãy biểu diễn mối
quan hệ giữa các khái niệm:
1. Sinh viên,đoàn viên TNCS HCM, sinh viên 5tốt,sinh
viên giỏi,cầu thủ bóng đá;
2. Trí thức,giảng viên đại học,kỹ sư,cử nhân,luật sư;
3. Tội phạm,tội xâm phạm tính mạng -sức khỏe -nhân
phẩm –danh dự,tội phạm kinh tế,tội vu khống,tội
buôn bán –vận chuyển hàng giả,tội trộm cắp tài sản.
4. Cá,cá biển,cá nước ngọt,cá da trơn,cá cảnh.
5. Cây lương thực,cây ăn quả,cây lúa,cây cam, cây
dừa.11
1/22/20
I.4. Quan hệ giữa các KN
CHƯƠNG 2-KHÁI NIỆM
12
1/22/20
II. CÁC THAO TÁC LOGIC ĐỐI VỚI KHÁI NIỆM
II.1. Các thao tác logic đối với ngoại diên
II.2. Mở rộng và thu hẹp khái niệm
II.3. Định nghĩa khái niệm
II.4. Phân chia khái niệm
5
A, B
A, B đồng nhất A lệ thuộc B
B
A
A, B đối chọi
AB
A, B mâu thuẫn
AB
C
A, B giao nhau
A B
Phép hợp
(cộng)
A độc lập B
B
A
II.1. Thao tác logic đối với ND
A ∪ B = A = B = B ∪ A A ∪ B = B = B ∪ A
A ∪ B = B ∪ A = C
A ∪ B = B = B ∪ A
Cả phần giao nhau của A và B
C
A, B
A, B đồng nhất A lệ thuộc B
B
A
A, B mâu thuẫn
AB
A, B đối chọi
ABC
A, B giao nhau
A B
Phép giao
(nhân)
A độc lập B
B
A
II.1. Thao tác logic đối với ND
𝐴 ∩ B = B ∩ A =
Phần giao nhau của A và B
C
A, B
A, B đồng nhất A lệ thuộc B
B
A
A, B mâu thuẫn
AB
A, B đối chọi
ABC
A, B giao nhau
A B
Phép trừ
A độc lập B
B
A
II.1. Thao tác logic đối với ND
A − B =(Phần gạch chéo của A)
B − A = (Phần gạch chéo của B)
𝐵 − A = (Phần gạch
chéo của B)
A − B = ∅
C