Bài giảng Lý thuyết trường điện từ: Chương 3 - TS. Nguyễn Việt Sơn

Bài giảng Lý thuyết trường điện từ: Chương 3 - Dịch chuyển điện, viết bởi TS. Nguyễn Việt Sơn, mô tả về khái niệm dịch chuyển điện và luật Gauss trong lĩnh vực điện từ. Học thuật này giúp người đọc hiểu rõ hơn về khái niệm và công thức toán học trong lĩnh vực.

Đối tượng đáng tiếp cận cho bài giảng Lý thuyết trường điện từ: Chương 3 - Dịch chuyển điện - Luật Gauss - Dive là những người có kinh nghiệm và muốn tìm hiểu thêm về lý thuyết trường điện từ, bao gồm nhà nghiên cứu học viện, doanh nghiệp kỹ thuật số và các nhóm phát triển chính sách.

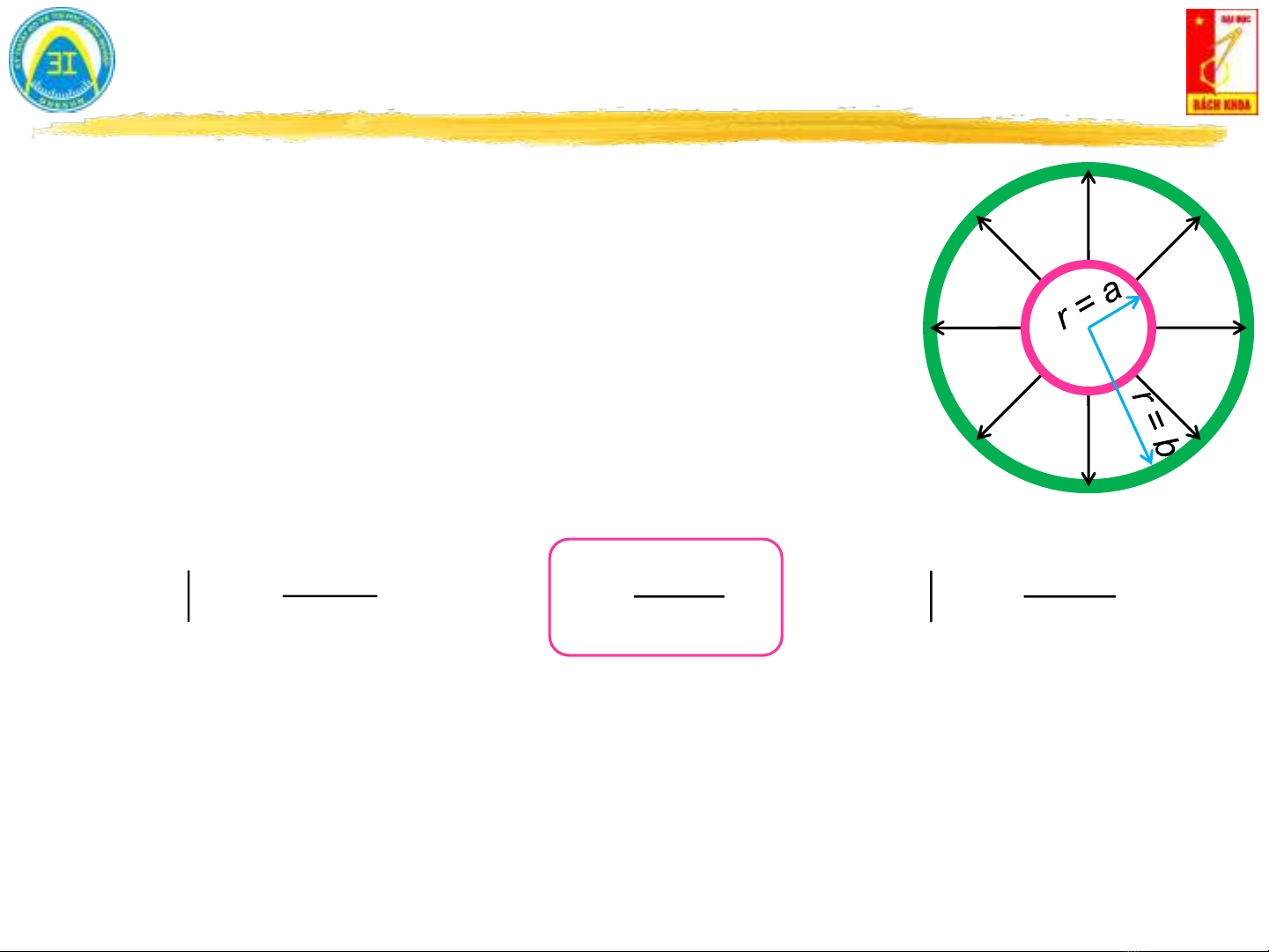
Tài liệu Lý thuyết trường điện từ: Chương 3 - Dịch chuyển điện - Luật Gauss - Dive là một bài giảng học thuật về lý thuyết trường điện từ, nói rằng dịch chuyển điện là khái niệm quan trọng trong điện từ. Tài liệu giới thiệu cách tính vector mật độ dịch chuyển điện và cách áp dụng luật Gauss để tính toán kinetic energy in electric circuits. Luật Gauss được trình bày với sự áp dụng trên nhiều ví dụ, bao gồm thí nghiệm của M. Faraday và ví dụ 3.1 về tính tổng thông lượng qua hình lập phương. Ngoài ra, khái niệm điện tích điểm, điện tích đường và điện tích mặt đã được giới thiệu trong bài giảng. Từ kết luận của tài liệu, thí nghiệm của M. Faraday đã được kiểm chứng bằng luật Gauss và đóng góp của Gauss không phải phát biểu luật mà tìm ra công thức toán học cho luật. Với nội dung hữu ích, bài giảng được sử dụng cho người đọc có kinh nghiệm và muốn tìm hiểu thêm về lý thuyết trường điện từ.