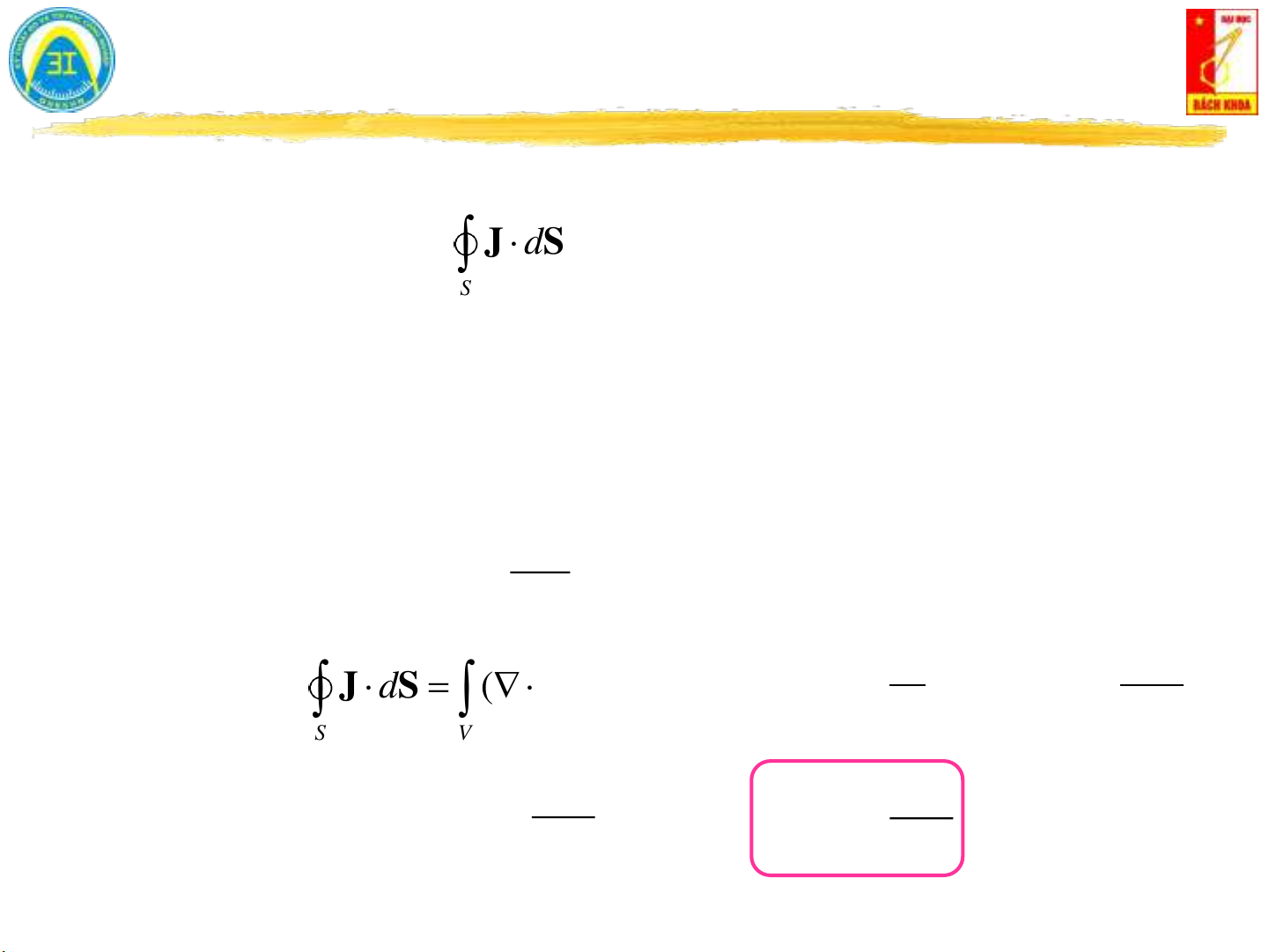Bài giảng Lý thuyết trường điện từ: Chương 5 - TS. Nguyễn Việt Sơn

Bài giảng 'Lý thuyết trường điện từ: Chương 5 - Vật dẫn, điện môi, điện dung' là một bài giảng học thuật chứng minh sự phát triển của lý thuyết trường điện từ với nội dung liên quan đến dòng điện, vật dẫn kim loại và ứng dụng thực tế.

Nhà nghiên cứu và sinh viên đang học lý thuyết trường điện từ

Bài giảng 'Lý thuyết trường điện từ: Chương 5 - Vật dẫn, điện môi, điện dung' của TS. Nguyễn Việt Sơn thảo luận về những yếu tố cơ bản của điện từ, bao gồm dòng điện, mật độ dòng điện, vật dẫn kim loại, chất điện môi, điện dung và phương pháp tính toán của nó. Bài giảng cho thảo luận về định lý Dive và nguyên tắc tính mật độ dòng điện qua mặt kín, cấu tạo của nguyên tử và diện tích diện tượng. Bài giảng cũng đề cập đến phương pháp soi ảnh, lưới, đường sức - đẳng thế và hầu hết các ứng dụng đó. Bài giảng tổng quát mô tả về những khái niệm, định lý và ứng dụng thực tế của lý thuyết trường điện từ.