Bài giảng Máy thủy khí - Chương 2: Máy cánh dẫn - bơm ly tâm

Chia sẻ: Nguyễn Thị Ngọc Lựu | Ngày: | Loại File: PDF | Số trang:38

Thêm vào BST

Báo xấu

662
lượt xem 165
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Bài giảng Máy thủy khí - Chương 2: Máy cánh dẫn - bơm ly tâm trình bày các nội dung: khái niệm chung về máy cánh dẫn, kết cáu, nguyên lý làm việc của bơm ly tâm, nguyên lý làm việc của bơm ly tâm, phân loại bơm ly tâm, phương trình cơ bản của máy cánh dẫn, các thành phần vận tốc CL qua BCT, phương trình cột áp, ảnh hưởng của hình dạng cánh đến phân bố năng lượng, đường đặc tính của BLT,... Đây là tài liệu tham khảo dành cho sinh viên ngành Cơ khí - Chế tạo máy.

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Bài giảng Máy thủy khí - Chương 2: Máy cánh dẫn - bơm ly tâm

Chương 2 MÁY CÁNH D N - BƠM LY TÂM 1 §1 Khái ni m chung v MCD - K t c u, nguyên lý làm vi c c a BLT Bơm và ñ ng cơ ki u cánh d n: • Bơm ly tâm, bơm hư ng tr c • Các lo i Tuabin : TB tâm tr c (Francis), TB hư ng tr c (Kaplan), TB gáo (Pelton) • Qu t, máy nén ly tâm, hư ng tr c -- Ly tâm (hư ng tâm): CL chuy n ñ ng qua BCT theo phương t tâm BCT ra ngoài (ho c t ngoài vào tâm theo phương bán kính). -- Hư ng tr c: CL chuy n ñ ng qua BCT theo phương song song v i tr c (d c tr c) 2 1
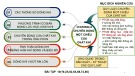
K t c u Bơm ly tâm • Bánh công tác: ñĩa (may ơ) l p trên tr c, trên may ơ g n các cánh d n. Cánh d n là các b n cong. BCT có chuy n ñ ng quay. • BCT ñ t trong v bơm ( bu ng xo n: c a vào bu ng xo n n i v i ng hút, c a Bánh công tác ra bu ng xo n n i v i ng ñ y). 3 Bánh công tác bơm ly tâm 4 2
Bơm ly tâm 5 Sơ ñ V Bơm ly tâm C a ra Diffuseur Bu ng xo n http://www.civil.usherbrooke.ca/cours/gci435/Pompes%20centrifuges1_files/frame.htm 6 3
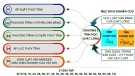
Bơm ly tâm - Nguyên lý làm vi c 4 6 3 1 2 Đĩa A Đĩa B Cánh d n 7 Nguyên lý làm vi c Đi u ki n: Bu ng xo n, bánh công tác và ng hút ph i ñư c ñi n ñ y ch t l ng (m i bơm). Nguyên lý làm vi c: • BCT quay CL trong BCT ñư c cánh d n cung c p năng lư ng; l c ly tâm ñ y CL ñi ra kh i BCT CL ñư c gom vào bu ng xo n và ñi vào ng ñ y: quá trình ñ y c a bm. • CL ñi ra kh i BCT c a vào c a BCT t o nên 1 vùng có chân không hút CL t b hút theo ng hút vào BCT: quá trình hút c a bm. • Quá trình hút và ñ y là liên t c, ñ ng th i t o nên dòng ch y liên t c trong h th ng ñ ng ng. 8 4
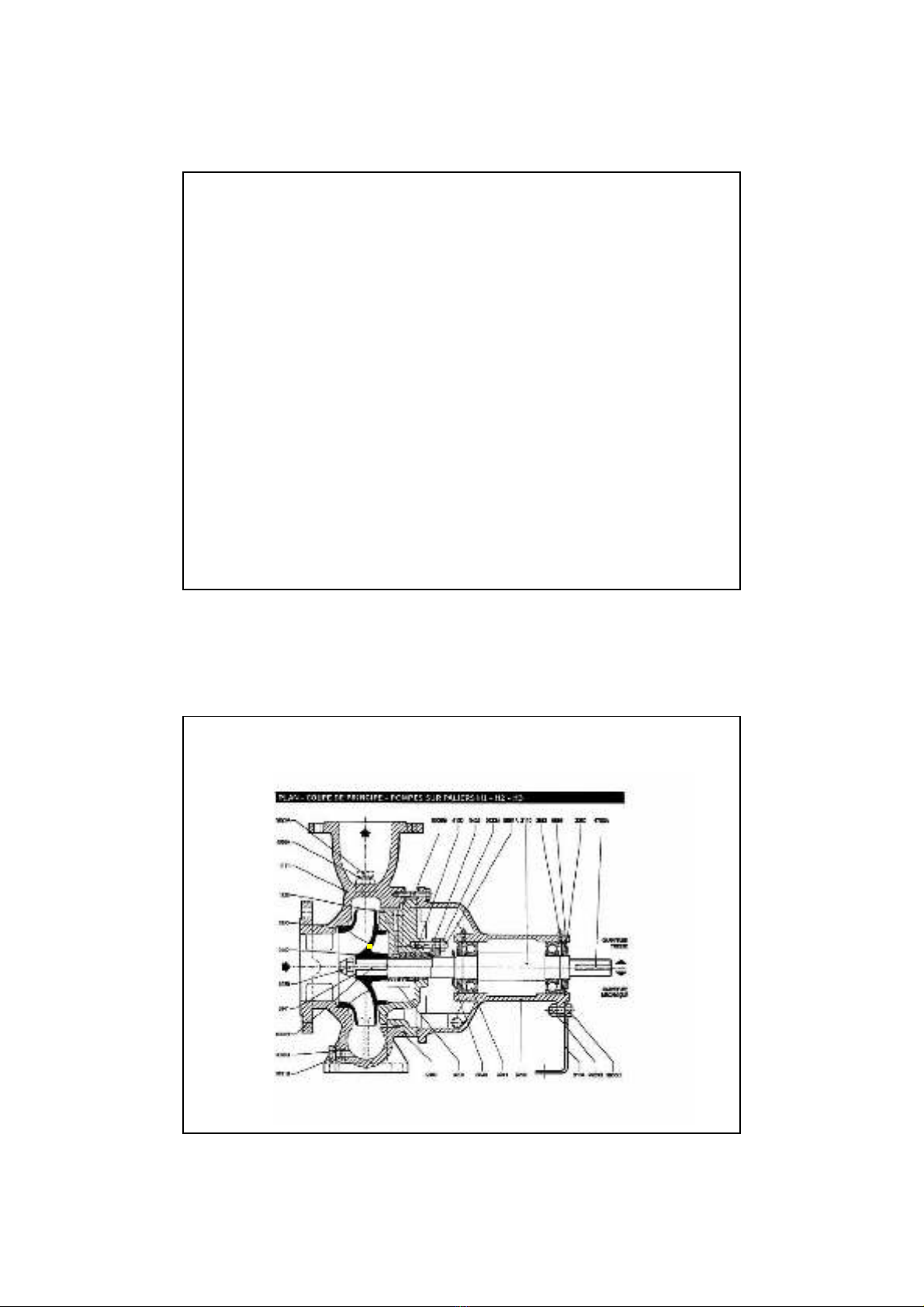
Phân lo i • Bơm 1 c p, 1 mi ng hút: - 1 BCT - c t áp b h n ch do s c b n (≤ 100m c t nư c). • Bơm nhi u c p: - T o c t áp cao - Nhi u BCT l p trên 1 tr c chung. - C t áp là t ng c a các c t áp do các BCT ñơn t o nên. • Bơm hai mi ng hút: - Hút CL vào t 2 phía, - BCT bao g m 2 BCT c a bơm 1 mi ng hút ñ i x ng nhau ghép l i, - Lưu lư ng c a bơm tăng g p ñôi - C t áp b ng c t áp c a bơm 1 mi ng hút . 9 Bơm ly tâm 1 c p, 1 mi ng hút 10 5
Bơm ly tâm 1 c p, 2 mi ng hút 11 Bơm ly tâm nhi u c p 12 6
Tr c Bơm ly tâm nhi u c p 13 §2. Phương trình cơ b n c a máy cánh d n • Quan h gi a c t áp H do BCT t o ra v i các thông s hình h c (ñư ng kính BCT, ñ cong c a cánh...) và các thông s ñ ng h c (s vòng quay, lu l ng) cu BCT 14 7
I. Gi thi t Euler 1. Dòng ch y qua BCT g m các dòng nguyên t gi ng h t nh nhau. 2.Chuy n ñ ng tương ñ i c a ch t l ng trong BCT có qu ñ o trùng khít v i biên d ng cánh d n. Đi u ki n ñ có dòng ch y như gi thi t trên: + S cánh d n nhi u vô cùng và m ng vô cùng. + CL làm vi c là CL lí tư ng (không nh t) C t áp tính toán v i các gi thi t trên: c t áp lý thuy t - vô cùng Hl∞ ∞ 15 Bánh công tác bơm ly tâm 16 8
II. Các thành ph n v n t c c a CL qua BCT Ký hi u: 1: v trí CL b t ñ u vào BCT (g p cánh): R1 2: v trí CL khi ra kh i BCT (ra kh i cánh): R2 • Chuy n ñ ng theo (quay cùng BCT): v n t c theo (v n t c vòng), có phương th ng góc v i bán kính t i ñi m ñó. ω u1=ω.R1 ω u2=ω.R2 • Chuy n ñ ng tương ñ i: v n t c tương ñ i ti p tuy n v i cánh d n w1, w2 • Chuy n ñ ng tuy t ñ i: v n t c tuy t ñ i c1, c2 c=u+w 17 Các thành ph n v n t c c a CL trong BCT bơm ly tâm b 2 1 ω 18 9
Velocity diagrams 19 Tam giác v n t c • β : góc gi a w và phương ngư c chi u v i u (góc b trí cánh d n trên bánh công tác) β1 : góc ñ t cánh t i c a vào β2 : góc ñ t cánh t i c a ra c2 w2 • cu : hình chi u c a c lên c2m phương u β2 • cm : hình chi u c a c lên u2 c2u phương th ng góc v i u. 20 10
• C2m ⊥ ti t di n ch y ra c a BCT C2m là thành ph n v n t c t o ra lưu lư ng • Cu là thành ph n v n t c nh hư ng ñ n c t áp Q Q c2 m = = F2 2π ⋅ r2 ⋅ b2 w2 c2 c2m β2 cu = u − cm ⋅ ctgβ u2 c2u 21 III. Phương trình c t áp (PT cơ b n c a máy cánh d n) ⋅ (u 2 ⋅ c 2 u − u 1 ⋅ c1u ) 1 • Bơm H l∞ = g ⋅ (u 1 ⋅ c1u − u 2 ⋅ c 2 u ) 1 • Tua bin H l∞ = g 22 11
Ý nghĩa c a phng trình c b n 1. Quan h gi a các thành ph n v n t c v i c t áp: • Tam giác v n t c: w22 = c22 + u22 - 2 u2. c2u u 2 . c 2u = 2 (c2 + u22 − w 22) 1 2 = ( c1 2 + u 1 2 − w 1 2 ) 1 u1 . c1u 2 H l∞ = 1 2g 2 [( c2 + u2 − w2 − c1 + u1 − w1 2 2 2 2 2 ) ( )] c − c1 u2 − u1 w1 − w2 2 2 2 2 2 2 = 2 + + 2g 2g 2g 23 H l∞ = 1 2g 2 [( c2 + u2 − w2 − c1 + u1 − w1 2 2 2 2 2 ) ( )] c − c1 u2 − u1 w1 − w2 2 2 2 2 2 2 = 2 + + 2g 2g 2g u 2 2 − u1 2 w 1 2 − w 2 2 c 2 2 − c1 2 H l∞ténh = + H l∞âäüng = 2g 2g 2g ⇒ Hl∞ ∞ = Hl∞tĩnh + Hl∞ñ ∞ ∞ ng -C t áp ñ ng: ph n ñ ng năng ñơn v c a dòng ch y ñư c tăng lên khi ñi qua bơm. -C t áp tĩnh: do s chênh l ch c a u, w c a dòng ch y t il i vào và l i ra c a BCT. 24 12
2. N u c1u= 0: ñk ch y vào th ng góc (c1 vuông góc v i u1) c1 = c1m = w1 − u1 2 2 2 2 ⋅ ( u 2 ⋅ c 2u ) 1 H l∞ = g Đi u ki n có l i nh t v c t áp ñ i v i B, Q, MN 25 3. C t áp th c H: H < Hl∞ do: ∞ • T n th t năng lư ng do ch t l ng th c • S cánh d n là h u h n (Z cánh) H = ηH . εZ .Hl∞ ∞ • ηH :hi u su t th y l c (0,8 ÷ 0,96) bi u th t n th t năng lư ng khi dòng ch y ñi TRONG BCT. • εZ: h s nh hư ng do s cánh là h u h n. π εZ = 1 − sin β 2 Z - Công th c Stodola; Z là s cánh c a BCT) - Trong tính toán g n ñúng: εZ = 0,8 26 13
K t lu n • H t l v i: - Đư ng kính ra D2 - S vòng quay n - V n t c c2u t i l i ra c a BCT • H b gi i h n do: - Svq n h n ch b i kh năng ch ng xâm th c - D2 không ñư c quá l n - c2u không ñư c quá l n (c2 quá l n => t n th t năng lư ng c a dòng ch y qua BCT s r t l n) => nh hư ng ñ n hi u su t c a bơm. mu n c t áp là có l i nh t thì BCT ph i có: - k t c u phù h p - góc b trí cánh d n h p lý. 27 Tính toán sơ b u2 H=Ψ 2 Ψ: h s c t áp th c 2 ns 50 ÷ 60 60 ÷ 180 180 ÷ 350 350 ÷ 580 BLT; H cao BLT; H trung BLT; H th p Bơm hư ng bình chéo Ψ 1,56 ÷ 1,24 1,24 ÷ 0,71 0,71 ÷ 0,51 0,41 ÷ 0,33 28 14
IV. nh hư ng c a hình d ng cánh ñ n s phân b năng lư ng 1) nh hư ng c a góc β1 Đi u ki n ch y vào th ng góc: c1u=0 w1 c1m c c tgβ1 = = 1m = 1 c1 u 1 − c1u u1 u1 u1 Q Q c1 m = ⇒ tgβ1 = πD1 b1 µ 1 πD1 b1 µ 1 u1 µ1 = 0,85 ÷ 0,95: h s nh hư ng c a chi u dày cánh Đ dòng ch y không va ñ p v i cánh d n t i l i vào c a BCT, ( nh hư ng x u ñ n hi u su t và c t áp th c): β1 = 15÷ 30o29 ÷ Các thành ph n v n t c c a CL trong BCT bơm ly tâm b 2 β2>90o 1 w2 ω u2 c2 30 15
2) nh hư ng c a góc ñ t cánh β2 ñ n c t áp ⋅ ( u 2 ⋅ c 2u ) 1 Đi u ki n ch y vào th ng góc H l∞ = g u2 ⋅ (u2 − c2 m ⋅ ctgβ 2 ) u2 u2 ⋅ c2 m 2 H l∞ = = − ⋅ ctgβ 2 g g g u a. Hl∞ > 0 β2 > β2min β 2 min = arc ctg 2 c2 m β2 0 β2min 90 180 Hl ∞ -∞ 0 u2 2 +∞ g 31 • nh hư ng c a góc β2 ñ n c t áp tĩnh c a bơm c1u=0 c1m=c2m=cm c 2 − c12 c 2 − c12m c 2 − c 2m H l∞âäüng = 2 = 2 = 2 2 2g 2g 2g c2 (u − c 2m ⋅ ctgβ 2 ) 2 w2 c2m H t∞âäüng = 2 β2 2g u2 c2u u2 ⋅ c2u (u 2 − c2 m ⋅ ctgβ 2 ) 2 H l∞tinh = H l∞ − H l∞dong = − g 2g u2  u2   u  H l∞ténh ≥ 0 ⇒ ctgβ 2 ≤ 2 ⇒ β 2 ≤ arc ctg −  vaì β 2 ≥ arc ctg 2  2 2 c 2m  c 2m   c 2m  β2min
u2 ⋅ (u2 − c2 m ⋅ ctgβ 2 ) u2 u2 ⋅ c2 m 2 H l∞ = = − ⋅ ctgβ 2 g g g β2 0 β2min 90o β2max 180 Hl ∞ -∞ 0 u2 2 2u 2 2 +∞ g g Hl∞tĩnh -∞ 0 u2 2 0 -∞ 2g u2 2u 2 Hl∞ñ ng -∞ 0 2 2 +∞ 2g g 33 H l∞ténh • H s ph n l c: ñánh giá kh ρ= năng t o ra c t áp tĩnh H l∞ u 2 − (c 2m ctgβ 2 ) 2 2 2g 1  c 2m  ρ= = 1 + ctgβ 2  u − u 2 c 2m ctgβ 2 2 2 2 u2  g thì 1 c u  Cánh ngo t trư c: khi β2= β2max ρ= 1 − 2 m ⋅ 2  = 0 2 u 2 c 2m  Cánh hư ng kính: β2 = 90o ρ = 0,5 Cánh ngo t sau: β2
Đ i v i bơm ly tâm: • Hl∞tĩnh = (0,7 ÷ 0,8) H l∞ • Hl∞ñ ng = (0,2 ÷ 0,3) Hl∞ β2 = 15 ÷ 35o, trư ng h p ñ c bi t có th ch n β2 = 50o N u BLT có góc β2 ngoài ph m vi trên t n th t năng lư ng trong bơm quá l n, hi u su t r t th p: không ch p nh n. 35 §3. Đư ng ñ c tính c a BLT I. Đ ng ñ c tính c a bm: Bi u di n quan h gi a c t áp H theo lưu lư ng Q khi s vòng quay c a tr c bơm n=const. 1. Đư ng ñ c tính lý thuy t: Hlt ∞ [n=const] 36 Q 18
2. Đư ng ñ c tính th c: H Hlt∞ ∞ Hlt Atk H(Q) [n=const] ηmax η(Q) [n=const] QAtk Q Q[l/s] 0 2 4 6 8 10 12 14 H[m] 15 15,5 15,7 15 14 12 10 8 37 η% 0 40 60 74 78 70 60 40 II. Xác ñ nh ñi m làm vi c c a bm trong h th ng l i Qbơm = Qlư i Hbơm = Hlư i Hlæåïi(Q) ⇒ giao ñi m A A c a ñư ng ñ c H tính bơm và HBåm(Q) ñư ng ñ c tính [n=const] lư i Qbơm = QA ; Hbơm = HA ηA η(Q) γQ A H A N tr = [n=const] ηA Q 38 19
III. Đi u ch nh ch ñ làm vi c c a bm trong h th ng l i • Đi u ch nh ñ bm cung c p cho h th ng lư i lưu lư ng Q' theo yêu c u; • Đi u ch nh van trên ñư ng ng ñ y, gi nguyên s vòng quay c a bơm ñ c tính lư i thay ñ i (ζñ → ζ'ñ), ñ c tính bơm không ζ thay ñ i: : ñi m làm vi c A’ ñ c xác ñ nh trên ñ ng ñ c tính bm. • Thay ñ i s vòng quay c a tr c bơm ñ c tính bm thay ñ i, ñ c tính lư i không thay ñ i : ñi m làm vi c An’ ñ c xác ñ nh trên ñ ng ñ c tính l i. 39 1. Đi u ch nh van trên ñư ng ng H’læåïi(Q) ñ y: A’ ñư c Hlæåïi(Q) xác ñ nh trên H' A' A ñư ng ñ c H tính bơm. HBåm(Q) 2. Thay ñ i s HAn' An' HBåm(Q) [n=const] vòng quay [n’