1
MÔ PHỎNG MONTE CARLO
CHƯƠNG 4
Financial Modeling 1
4.1 GIỚI THIỆU
•Mô phỏng so với tối ưu hóa:
•Trong một mô hình tối ưu hóa, mô hình sẽ
cho ra tập hợp các giá trịcủa biến sốra quyết
định đểtối đa hóa hay tối thiểu hóa giá trịcủa
hàm mục tiêu.
•Trong một mô hình mô phỏng, mô hình sẽ
đánh giá các giá trịhàm mục tiêu đạt được
theo sựthay đổi của tập hợp các giá trịđầu
vào này.
Financial Modeling 2
2
4.1 GIỚI THIỆU
•Mô phỏng và các biến ngẫu nhiên
•Các mô hình mô phỏng thường được sửdụng đểphân
tích một quyết định trong điều kiện có rủi ro, đó là một mô
hình mà khảnăng biến động một hay nhiều các yếu tốcủa
mô hình là không biết được một cách chắc chắn.
•Các nhân tốmà ta không biết được một cách chắc chắn
được hiểu nhưlà biến ngẫu nhiên. Hành vi thay đổi của
một biến ngẫu nhiên được mô tảbởi phân phối xác suất.
•Loại hình mô phỏng này đôi khi được gọi là phương pháp
Monte Carlo, sau đó là phương pháp bánh xe Roulette, là
phương pháp có thểđược hiểu nhưlà cấu hình tạo lập
nên các sựkiện ngẫu nhiên hay không chắc chắn.
Financial Modeling 3
4.2 THIẾT LẬP CÁC BIẾN NGẪU NHIÊN
•Biến ngẫu nhiên liên tục:
Các biến ngẫu nhiên nhận các giá trịliên tục, không có bất cứ
khoảng cách nào giữa các biến ngẫu nhiên.
Ví dụ: bánh xe quay sốsau:
•Biến ngẫu nhiên rời rạc:
Các biến ngẫu nhiên chỉnhận một sốlượng giới hạn các giá
trị. Ví dụ: lượng cầu của một sản phẩm, sốlượng nhân
công cần thiết
Financial Modeling 4
0
0,75
0,5
0,25
3
4.2 THIẾT LẬP CÁC BIẾN NGẪU NHIÊN
•Các dạng phân phối xác suất:
•Phân phối đồng dạng: các giá trịngẫu nhiên trong khoảng
(min, max) có xác suất xảy ra bằng nhau.
•Phân phối chuẩn: một giá trịngẫu nhiên sẽcó xác suất xảy
ra cao nhất (giá trịtrung bình). Các giá trịtrên hay dưới giá
trịtrung bình có xác suất xảy ra nhưnhau (cân đối).
•Phân phối nhịthức: Chỉxảy ra hai giá trịvà có kết quảđộc
lập lẫn nhau.
•Phân phối lognomal: Biến có thểtăng vô hạn nhưng không
thểnhỏhơn 0. Log của biến có phân phối chuẩn.
•Và rất nhiều các dạng phân phối xác suất khác.
Financial Modeling 5
4.2 THIẾT LẬP CÁC BiẾN NGẪU NHIÊN
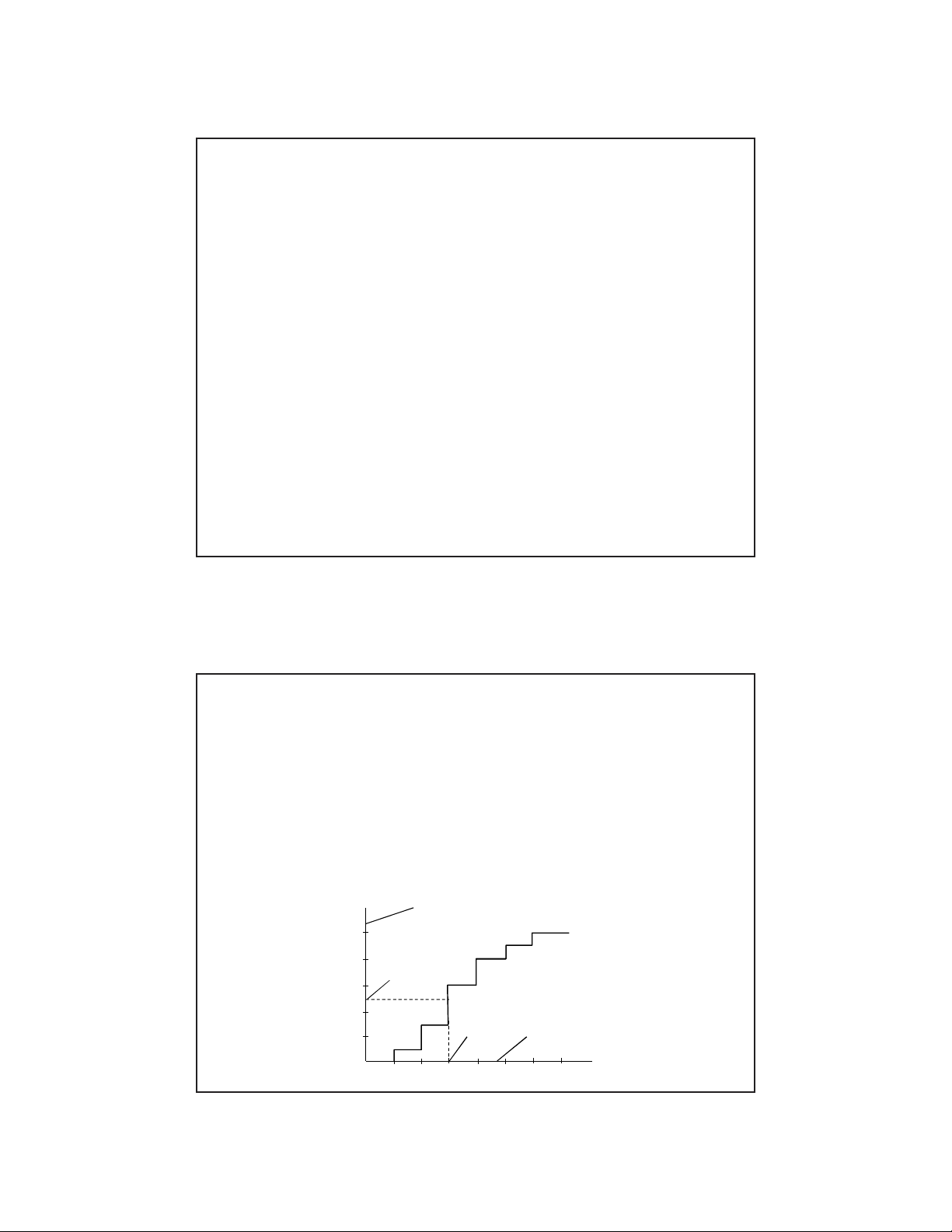
•Hàm phân phối tích lũy
•Hàm phân phối tích lũy được định nghĩa nhưlà xác suất mà
giá trịD nhỏhơn hoặc bằng x hay F(x) = Prob{D ≤ x}.
•Đồthịphân phối tích lũy:
Financial Modeling 6
Xác
suất
x
0,2
0,4
0,6
0,8
1,0
8 9 10 11 12 13 14
F(x)
d
Bước 1: ðịnh vị giá trị ulên trục tung
Bước 2: ðọc giá trị ngẫu nhiên d
tương ứng trên trục hoành
u
4
4.2 MÔ PHỎNG VỚI BẢNG TÍNH THÔNG THƯỜNG
•Khung tình huống:
•Công ty Airbus đang cân nhắc các vấn đềliên quan đến tài chính vềkhảnăng bổ
sung thêm một nhánh sản phẩm mới.
•Chi phí khởi sựcho mô hình máy bay thếhệmới A3XXs được ước tính khoảng
150.000.000$. Dựbáo lượng cầu đối với máy bay A3XXs là 10 chiếc cho mỗi một
năm trong 4 năm vòng đời của dựán. Một chiếc máy bay mới sẽđược bán với
giá 35.000.000$. Chi phí cốđịnh được ước tính 15.000.000$ cho một năm, trong
khi đó chi phí biến đổi sẽkhoảng 75% trên doanh sốmỗi năm.
•Chi phí khấu hao chịu thuếđối với thiết bịmới sẽlà 10.000.000$ một năm trong
suốt vòng đời của dựán máy bay A3XXs là 4 năm. Giá trịcòn lại của thiết bịvào
cuối năm thứ4 của dựán xem nhưlà 0$.
•Chi phí sửdụng vốn của hãng Airbus là 10%, và thuếsuất thuếthu nhập doanh
nghiệp là 34%.
Financial Modeling 7
4.2 MÔ PHỎNG VỚI BẢNG TÍNH THÔNG THƯỜNG
•Câu hỏi thực tiễn:
•Công ty Airbus có nên thục hiện dựán này không?
•Nếu lượng cầu của loại máy bay này không chắc chắn như
giảđịnh ban đầu rằng lượng cầu trong năm sẽlà một
trong các giá trịsau: 8,9,10, 11 hoặc 12 sản phẩm và xác
suất xảy ra mỗi giá trịnày là bằng nhau. Hãy đánh giá rủi
ro dựán?
Cụthể:
•Giá trịtrung bình hoặc giá trịmong đợi của NPV là bao
nhiêu?
•Xác suất đểNPV có giá trịâm là bao nhiêu?
•Cách giải quyết: xây dựng mô hình mô phỏng dựán trên
trong điều kiện không chắc chắn.
Financial Modeling 8
5
4.2 MÔ PHỎNG VỚI BẢNG TÍNH THÔNG THƯỜNG
•Một sốlưu ý đối với chương trình mô phỏng bằng bảng
tính:
•Gia tăng con sốnhững phép thửlà khuynh hướng để
nhận được dựđoán tốt hơn giá trịmong đợi nhưng ngay
cảkhi với con sốphép thửlớn hơn thì vẫn tồn tại sai số
giữa giá trịbình quân mô phỏng và giá trịmong đợi đúng.
•Mô phỏng có thểcung cấp thông tin hữu ích từsựphân
phối các giá trịkết quảđạt được. Đây là những thông tin
rất có giá trịvà đôi khi kết quảnày không thểcó được từ
những phân tích giản đơn, hoặc thậm chí trong cảphân
tích rủi ro giá lên/giá xuống.
•Kết quảmô phỏng khá nhạy cảm theo những giảđịnh yếu
tốnhập lượng đầu vào.
Financial Modeling 9
4.5 TỐI ƯU HÓA TRONG ĐIỀU KIỆN KHÔNG CHẮC CHẮN
•Vấn đềđặt ra với các nhà quản lý là kết hợp giữa mô hình
mô phỏng và mô hình tối ưu.
•Công cụSolver đã làm việc rất hiệu quảkhi đi giúp chúng
ta đi tìm giải pháp tối ưu trong điều kiện chắc chắn theo
đó các biến nội sinh (biến sốđầu vào của mô hình) sẽtạo
ra giá trịhàm mục tiêu tối ưu.
•Các chương trình mô phỏng nhưCrytal Ball rất hữu ích
trong việc giải quyết các biến sốngoại sinh trong điều kiện
không chắc chắn.
•Kết hợp 2 công cụtrên nhà quản lý sẽgiải quyết được bài
toán tối ưu trong những điều kiện không chắc chắn.
•Phần này sẽgiới thiệu công cụOptQuest trong Crytal Ball
giải quyết vấn đềtrên.
Financial Modeling 10