intTypePromotion=1
zunia.vn Tuyển sinh 2024 dành cho Gen-Z zunia.vn zunia.vn
ADSENSE
 » 
 » 

Bài giảng Nhiệt động lực học và truyền nhiệt: Chương 8 - TS. Nguyễn Văn Hạp

Chia sẻ: _ _ | Ngày: | Loại File: PDF | Số trang:28

Thêm vào BST
Báo xấu
4
lượt xem 2
download
 
  Download Vui lòng tải xuống để xem tài liệu đầy đủ

Bài giảng Nhiệt động lực học và truyền nhiệt: Chương 8 - Dẫn nhiệt, được biên soạn gồm các nội dung chính sau: Khái niệm cơ bản về dẫn nhiệt; Định luật Fourier; Phương trình vi phân dẫn nhiệt của vật rắn; Điều kiện đơn trị; Dẫn nhiệt ổn định. Mời các bạn cùng tham khảo!

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Bài giảng Nhiệt động lực học và truyền nhiệt: Chương 8 - TS. Nguyễn Văn Hạp

  1. TS Nguyễn Văn Hạp – BM CN Nhiệt Lanh – ĐH Bách Khoa Tp.HCM LOGO Chapter 8: Dẫn nhiệt (Heat conduction) 8.1 Khái niệm cơ bản về dẫn nhiệt 8.2 Định luật Fourier 8.3 Phương trình vi phân dẫn nhiệt của vật rắn 8.4 Điều kiện đơn trị 8.5 Dẫn nhiệt ổn định CuuDuongThanCong.com https://fb.com/tailieudientucntt
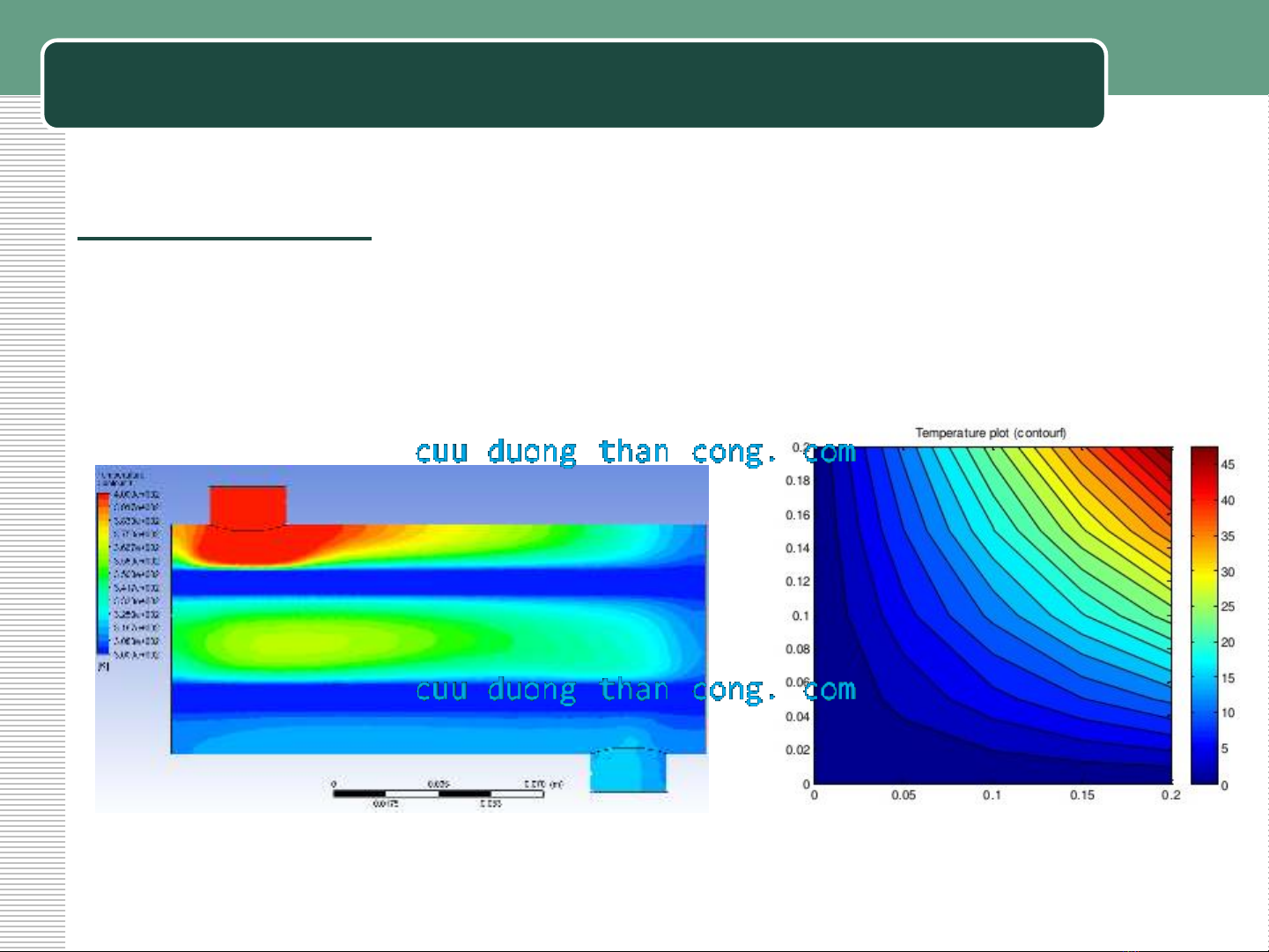
  2. TS Nguyễn Văn Hạp – BM CN Nhiệt Lanh – ĐH Bách Khoa Tp.HCM LOGO Chapter 8: Dẫn nhiệt (Heat conduction) 8.1 Khái niệm cơ bản về dẫn nhiệt Trường nhiệt độ: Nhiệt độ là thông số phụ thuộc không gian và thời gian t = f(x,y,z,) Tập hợp các giá trị của t trong không gian tại 1 thời điểm nào đó gọi là trường nhiệt độ. - Trường nhiệt độ ổn định: không phụ thuộc thời gian Một chiều: t = f(x) Hai chiều: t = f(x,y) Ba chiều: t = f(x,y,z) - Trường nhiệt độ không ổn định: phụ thuộc thời gian Một chiều: t = f(x, ) Hai chiều: t = f(x,y, ) Ba chiều: t = f(x,y,z, ) CuuDuongThanCong.com https://fb.com/tailieudientucntt
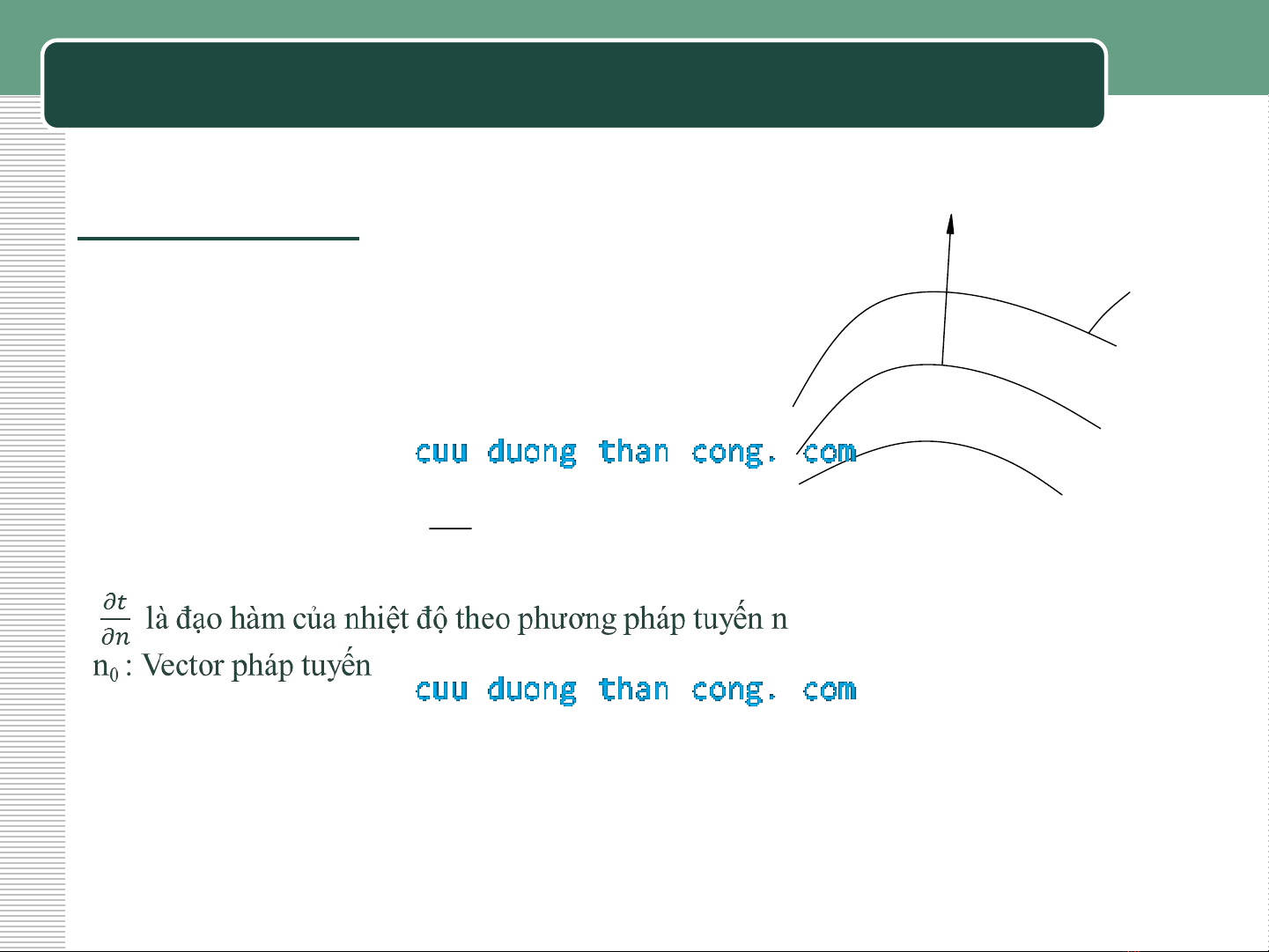
  3. TS Nguyễn Văn Hạp – BM CN Nhiệt Lanh – ĐH Bách Khoa Tp.HCM LOGO Chapter 8: Dẫn nhiệt (Heat conduction) 8.1 Khái niệm cơ bản về dẫn nhiệt MẶT ĐẲNG NHIỆT : Tập hợp các điểm có nhiệt độ như nhau tại một thời điểm nhất định của vật ta có mặt cùng nhiệt độ gọi là mặt đẳng nhiệt CuuDuongThanCong.com https://fb.com/tailieudientucntt
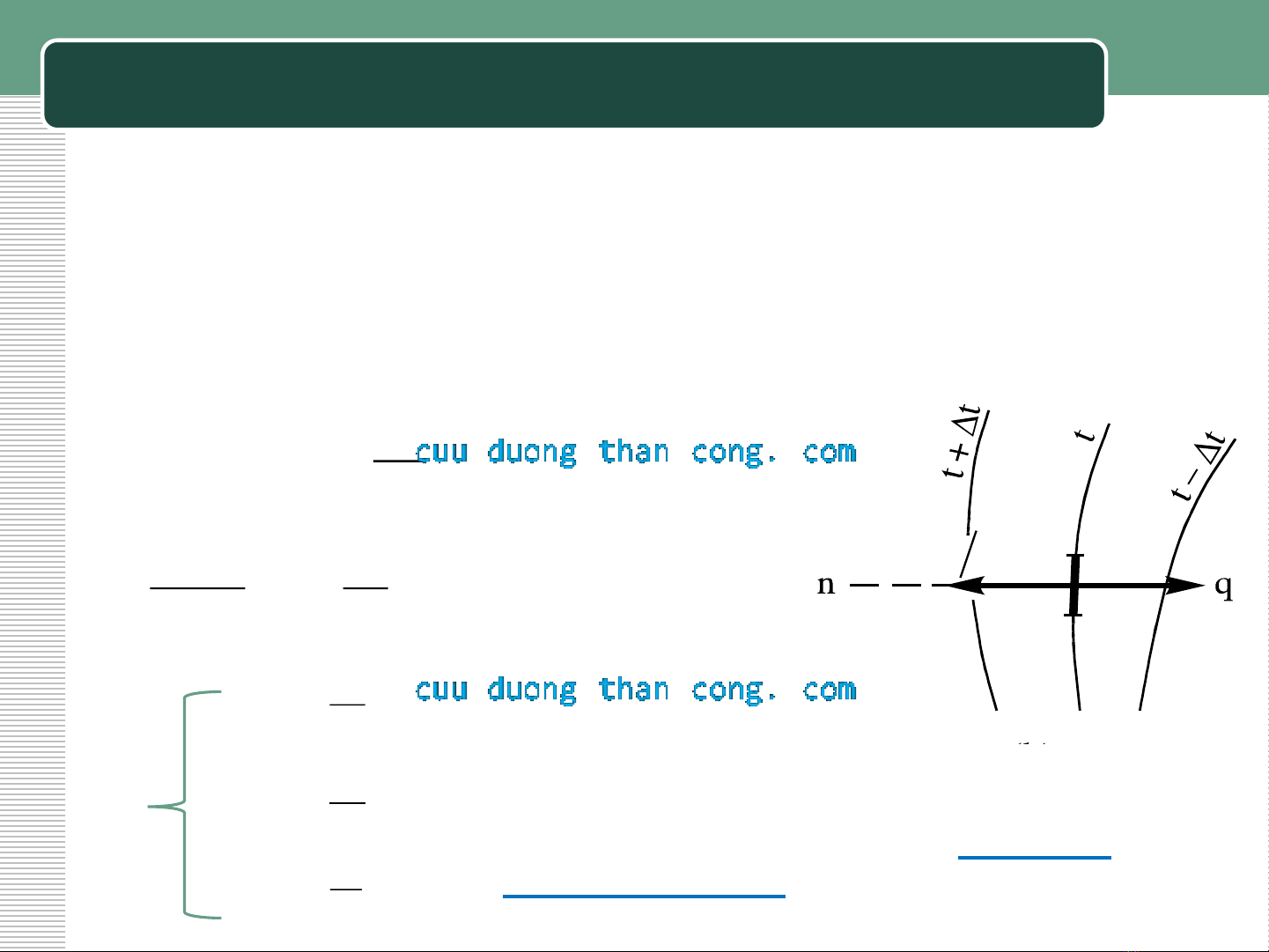
  4. TS Nguyễn Văn Hạp – BM CN Nhiệt Lanh – ĐH Bách Khoa Tp.HCM LOGO Chapter 8: Dẫn nhiệt (Heat conduction) 8.1 Khái niệm cơ bản về dẫn nhiệt Gradient nhiệt độ : n Nhiệt độ trong vật chỉ thay đổi theo phương cắt Maët ñaúng nhieät các mặt đẳng nhiệt. n t+t Biến thiên nhiệt độ theo phương pháp tuyến với bề mặt đẳng nhiệt là lớn nhất. t t t - t gradt  n0 n gradt cho biết đặc trưng biến thiên nhiệt độ theo phương pháp tuyến với mặt đẳng nhiệt. CuuDuongThanCong.com https://fb.com/tailieudientucntt
  5. TS Nguyễn Văn Hạp – BM CN Nhiệt Lanh – ĐH Bách Khoa Tp.HCM LOGO Chapter 8: Dẫn nhiệt (Heat conduction) 8.2 Định luật Fourier - Định luật Fourier sử dụng cho phương thức dẫn nhiệt - Phát biểu ĐL: Nhiệt lượng dQ truyền qua phần tử bề mặt đẳng nhiệt dF trong khoảng thời gian d tỷ lệ thuận với gradient nhiệt độ t dQ   n o  dFd n t t n   , W /m 2  dQ q dFd n t q x   q: Mật độ dòng nhiệt x t Nhiệt lượng truyền từ nơi có nhiệt độ cao q y   đến nơi có nhiệt độ thấp, vector gradt y ngược chiều với vectơ q,  biểu thức t trên mang dấu trừ. q z   z CuuDuongThanCong.com https://fb.com/tailieudientucntt
  6. TS Nguyễn Văn Hạp – BM CN Nhiệt Lanh – ĐH Bách Khoa Tp.HCM LOGO Chapter 8: Dẫn nhiệt (Heat conduction) 8.2 Định luật Fourier : Hệ số dẫn nhiệt  CuuDuongThanCong.com https://fb.com/tailieudientucntt
  7. TS Nguyễn Văn Hạp – BM CN Nhiệt Lanh – ĐH Bách Khoa Tp.HCM LOGO Chapter 8: Dẫn nhiệt (Heat conduction) 8.3 Phương trình vi phân dẫn nhiệt của vật rắn Để tính Q, ta cần biết trường nhiệt độ  Cần xác định PT trường nhiệt độ. Các giả thiết để lập phương trình vi phân dẫn nhiệt: + Vật đồng chất và đẳng hướng. + Thông số vật lý là hằng số. + Vật xem là hoàn toàn cứng, nghĩa là sự thay đổi thể tích do nhiệt độ gây nên rất bé. + Các phần vĩ mô của vật không có sự chuyển động tương đối với nhau. + Nguồn nhiệt bên trong phân bố đều là qv = f(x,y,z,) CuuDuongThanCong.com https://fb.com/tailieudientucntt
  8. TS Nguyễn Văn Hạp – BM CN Nhiệt Lanh – ĐH Bách Khoa Tp.HCM LOGO Chapter 8: Dẫn nhiệt (Heat conduction) 8.3 Phương trình vi phân dẫn nhiệt của vật rắn Xét phân tố thể tích dv=dx.dy.dz trong thời gian d. Dựa trên cơ sở định luật bảo toàn năng lượng và định luật Fourier:  Doøng nhieät   Doøng nhieät phaùt ra   Ñoä bieán thieân         ñöa vaøo phaân   trong phaân toá dxdydz   noä i naêng   toá dxdydz baèng   do nguoàn nhieät    trong phaân         daãn nhieät   beân trong phaùt ra   toá dxdydz        I II III Qv CuuDuongThanCong.com https://fb.com/tailieudientucntt
  9. TS Nguyễn Văn Hạp – BM CN Nhiệt Lanh – ĐH Bách Khoa Tp.HCM LOGO Chapter 8: Dẫn nhiệt (Heat conduction) 8.3 Phương trình vi phân dẫn nhiệt của vật rắn t   2t 2t 2t  qv   2  2  2   c  x  y z  c  t qv  a t  2  c Trong đó: 2t 2t 2t Toán tử Laplace  2  2  2t x 2 y z  Hệ số khuyếch tán nhiệt a c CuuDuongThanCong.com https://fb.com/tailieudientucntt
  10. TS Nguyễn Văn Hạp – BM CN Nhiệt Lanh – ĐH Bách Khoa Tp.HCM LOGO Chapter 8: Dẫn nhiệt (Heat conduction) 8.3 Phương trình vi phân dẫn nhiệt của vật rắn Hệ toạ độ trụ (r,, z): t   2 t 1 t 1  2 t  2 t  q v  a 2    2  2  2    r   r r r  z  c  Hệ toạ độ cầu (r, , ): t 1  2 1   t  1 2t  qv  a  2 rt   2   sin    2  r sin 2   2   c   r r r sin       CuuDuongThanCong.com https://fb.com/tailieudientucntt
  11. TS Nguyễn Văn Hạp – BM CN Nhiệt Lanh – ĐH Bách Khoa Tp.HCM LOGO Chapter 8: Dẫn nhiệt (Heat conduction) 8.4 Điều kiện đơn trị - Điều kiện hình học: hình dáng, kích thước - Điều kiện vật lý: Thông số vật lý (,  , c, …) và qui luật phân bố nguồn nhiệt bên trong (qv) - Điều kiện biên: điều kiện trao đổi nhiệt trên biên giới vật thể. Có 04 loại điều kiện biên: + Loại 1: biết nhiệt độ bề mặt (tw), chưa biết mật độ dòng nhiệt (q). + Loại 2: biết mật độ dòng nhiệt (q), chưa biết nhiệt độ bề (tw) CuuDuongThanCong.com https://fb.com/tailieudientucntt
  12. TS Nguyễn Văn Hạp – BM CN Nhiệt Lanh – ĐH Bách Khoa Tp.HCM LOGO Chapter 8: Dẫn nhiệt (Heat conduction) 8.4 Điều kiện đơn trị - Điều kiện biên: + Loại 3: Cho biết nhiệt độ môi trường (tf), và qui luật trao đổi nhiệt giữa bề mặt vật với môi trường xung quanh. Theo ĐL Newton-Ricman, nhiệt lượng tỏa ra trên 1 đơn vị diện tích bề mặt: Hệ số tỏa nhiệt α (W/m2.độ) Nhiệt lượng q này tiếp tục truyền trong vật bằng dẫn nhiệt:  t  t w  t f       n  w + Loại 4: cân bằng về dòng nhiệt qua chỗ bề mặt tiếp xúc  t   t  1     2   lý tưởng (Nhiệt độ hai bề mặt tại điểm tiếp xúc bằng nhau)  n  w  n  w CuuDuongThanCong.com https://fb.com/tailieudientucntt
  13. TS Nguyễn Văn Hạp – BM CN Nhiệt Lanh – ĐH Bách Khoa Tp.HCM LOGO Chapter 8: Dẫn nhiệt (Heat conduction) 8.4 Dẫn nhiệt ổn định t 2 qv 0 a t  0  c Nếu không tồn tại nguồn nhiệt bên trong (qv = 0):  2t  2t  2t 2t  0  2  2 0 x y 2 z Dẫn nhiệt ổn định 1 chiều như: + Truyền nhiệt qua vách, tường… + Truyền nhiệt qua ống dẫn hơi, nước nóng CuuDuongThanCong.com https://fb.com/tailieudientucntt
  14. TS Nguyễn Văn Hạp – BM CN Nhiệt Lanh – ĐH Bách Khoa Tp.HCM LOGO Chapter 8: Dẫn nhiệt (Heat conduction) 8.4 Dẫn nhiệt ổn định 8.4.1 Dẫn nhiệt qua vách phẳng d2t t  C1 x  C 2 2 0 dx Q t x0  t 1 B.C: t1 t x   t 2 t2  t1 t2   t1  t 2 R  t  t1  x  Theo định luật Fourier:  t t PT töông töï phöông trình q  gradt   dt q  t1  t 2  Hoặc q  1 2 ñònh luaät Ohm với dx   R=/ CuuDuongThanCong.com https://fb.com/tailieudientucntt
  15. TS Nguyễn Văn Hạp – BM CN Nhiệt Lanh – ĐH Bách Khoa Tp.HCM LOGO Chapter 8: Dẫn nhiệt (Heat conduction) 8.4 Dẫn nhiệt ổn định 8.4.1 Dẫn nhiệt qua vách phẳng Vách phẳng nhiều lớp:  1 q  1 t1  t 2  t1  t 2  q 1 1  2 q  2 t 2  t3  t 2  t3  q 2 2   q  3 t3  t 4  t3  t 4  q 3 3 3     t1  t4 t1  t4 t1  tn 1 t1  t 4  q 1  2  3  q 1  2  3  q     R1  R2  R3 n i  1 2 3    1 2 3  i 1 i CuuDuongThanCong.com https://fb.com/tailieudientucntt
  16. TS Nguyễn Văn Hạp – BM CN Nhiệt Lanh – ĐH Bách Khoa Tp.HCM LOGO Chapter 8: Dẫn nhiệt (Heat conduction) 8.4 Dẫn nhiệt ổn định 8.4.1 Dẫn nhiệt qua vách phẳng VD: Q= 3920 W CuuDuongThanCong.com https://fb.com/tailieudientucntt
  17. TS Nguyễn Văn Hạp – BM CN Nhiệt Lanh – ĐH Bách Khoa Tp.HCM LOGO Chapter 8: Dẫn nhiệt (Heat conduction) 8.4 Dẫn nhiệt ổn định 8.4.1 Dẫn nhiệt qua vách phẳng VD: A=0,5m2 Lamda = 0.8 Q=? (40W) CuuDuongThanCong.com https://fb.com/tailieudientucntt
  18. TS Nguyễn Văn Hạp – BM CN Nhiệt Lanh – ĐH Bách Khoa Tp.HCM LOGO Chapter 8: Dẫn nhiệt (Heat conduction) 8.4 Dẫn nhiệt ổn định 8.4.1 Dẫn nhiệt qua vách phẳng VD: Heat is transferred steadily to boiling water in the pan through its bottom. The inner surface of the bottom of the pan is given. The D=0,2m temperature of the outer surface is to be determined. t2 = ? Assumptions 1 Steady operating conditions exist since the surface (105,420C) temperatures of the pan remain constant at the specified values. 2 Thermal properties of the aluminum pan are constant. Properties The thermal conductivity of the aluminum is given to be  = 237 W/mC. CuuDuongThanCong.com https://fb.com/tailieudientucntt
  19. TS Nguyễn Văn Hạp – BM CN Nhiệt Lanh – ĐH Bách Khoa Tp.HCM LOGO Chapter 8: Dẫn nhiệt (Heat conduction) 8.4 Dẫn nhiệt ổn định 8.4.1 Dẫn nhiệt qua vách phẳng VD: The heat generated in the circuitry on the surface of a 3-W silicon chip is conducted to the ceramic substrate. The temperature difference across the t = ? chip in steady operation is to be determined. (0,320C) Assumptions 1 Steady operating conditions exist. 2 Thermal properties of the chip are constant. Properties The thermal conductivity of the silicon chip is given to be  = 130 W/mC. CuuDuongThanCong.com https://fb.com/tailieudientucntt
  20. TS Nguyễn Văn Hạp – BM CN Nhiệt Lanh – ĐH Bách Khoa Tp.HCM LOGO Chapter 8: Dẫn nhiệt (Heat conduction) 8.4 Dẫn nhiệt ổn định 8.4.1 Dẫn nhiệt qua vách phẳng A styrofoam ice chest is initially filled with 40 kg of ice at 00C. The time it VD: takes for the ice in the chest to melt completely is to be determined. Assumptions 1 Steady operating conditions exist. 2 The inner and outer surface temperatures of the ice chest remain constant at 00C and 80C, respectively, at all times. 3 Thermal properties of the chest are constant. 4 Heat transfer from the base of the ice chest is negligible. Properties The thermal conductivity of the styrofoam is given to be  = 0.033 W/mC. The heat of fusion of ice at 00C is 333.7 kJ/kg. Analysis Disregarding any heat loss through the bottom of the ice chest and using the average thicknesses. A  (40  3)(40  3)  4  (40  3)(30  3)  5365 cm2  0.5365 m2 Q_loss=4,72W Q_melting=13,348kJ t =32,7 days CuuDuongThanCong.com https://fb.com/tailieudientucntt
ADSENSE

CÓ THỂ BẠN MUỐN DOWNLOAD

LV.15: Bộ Đồ Án Tốt Nghiệp Chuyên Ngành Cơ Khí
65 tài liệu
2431 lượt tải
THÔNG TIN
TRỢ GIÚP
HỖ TRỢ KHÁCH HÀNG
Theo dõi chúng tôi

Chịu trách nhiệm nội dung:

Nguyễn Công Hà - Giám đốc Công ty TNHH TÀI LIỆU TRỰC TUYẾN VI NA

LIÊN HỆ

Địa chỉ: P402, 54A Nơ Trang Long, Phường 14, Q.Bình Thạnh, TP.HCM

Hotline: 093 303 0098

Email: support@tailieu.vn

Giấy phép Mạng Xã Hội số: 670/GP-BTTTT cấp ngày 30/11/2015 Copyright © 2022-2032 TaiLieu.VN. All rights reserved.

 

Đồng bộ tài khoản
2=>2