PGS. TS. Trương Tích Thiện
ÔN TẬP- ĐỘNG HỌC
1. Hệ bánh răng hành tinh và vi sai
Định nghĩa
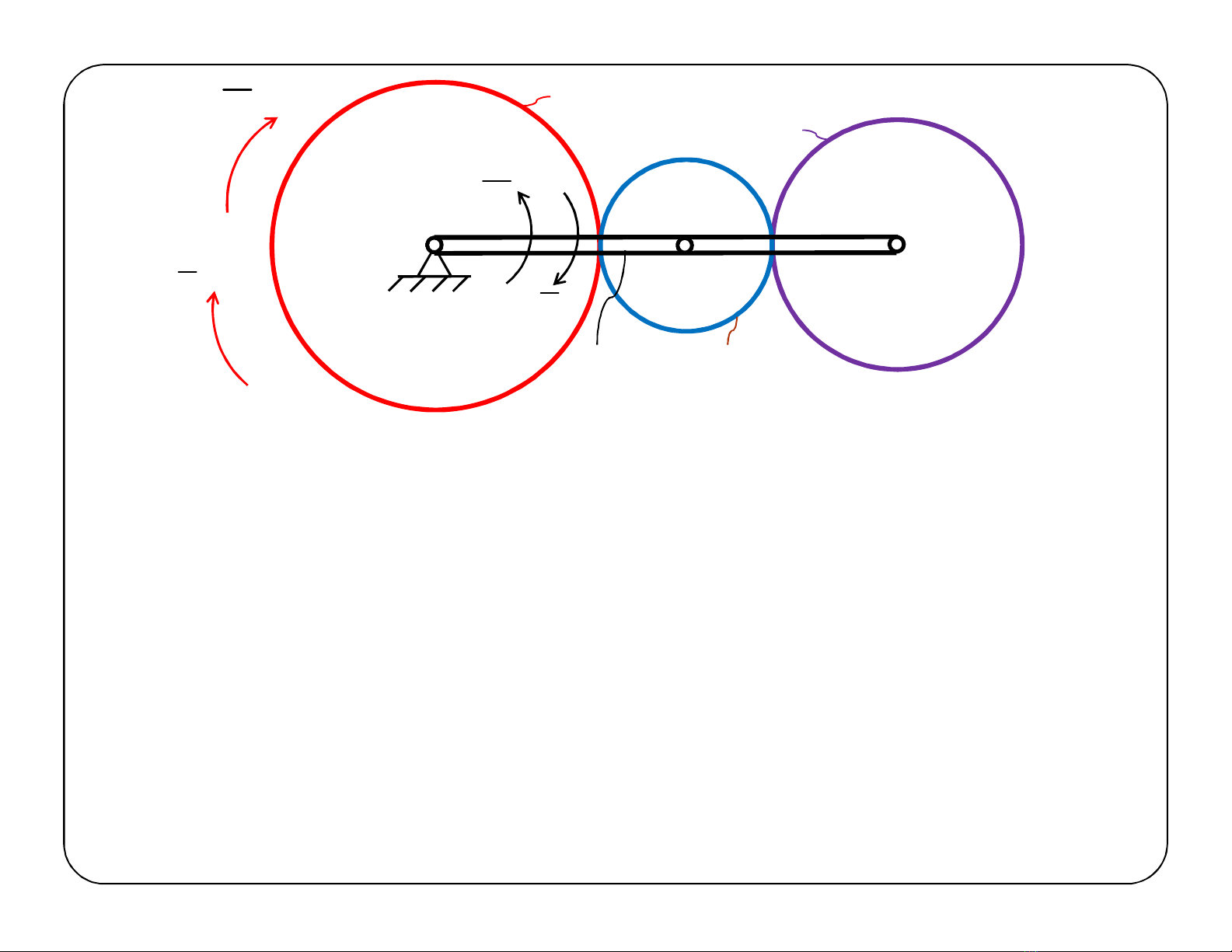
Là một hê nhiều vật rắn có dạng các đĩa tròn lăn không trượt
với nhau sao cho tối thiểu có 1 đĩa tròn có tâm quay chuyển
động. Vật rắn mang tâm quay của các bánh răng chuyển
động được gọi là cần và cần sẽ có chuyển động quay xung
quanh tâm O1cô định. Bánh răng có cùng tâm quay cô định
với cần được gọi là bánh răng trung tâm 1. Cần và bánh răng
trung tâm 1 có dạng chuyển động cơ bản : quay quanh tâm
quay cô định O1. Hai chuyển động quay của 2 vật rắn này
hoàn toàn độc lập với nhau. Các bánh răng còn lại sẽ có
dạng chuyển động song phẳng.
1
O2
O3
O
1
①
②
③
1
c
c
cần
Nếu bánh răng trung tâm 1 được giư cô định thi hê được gọi là
hê bánh răng hành tinh. Bậc tư do của hê bánh răng hành tinh
= +1. Dofht = +1.
Nếu cần được giữ cô định thi hê bánh răng sẽ trơ thành hê
bánh răng thường.
Nếu bánh răng trung tâm 1 có chuyển động quay quanh tâm
quay O1cô định độc lập với chuyển động quay của cần thi hê
se được gọi là hê bánh răng vi sai. DofVS = +2.
2. Động học hệ bánh răng hành tinh và vi sai
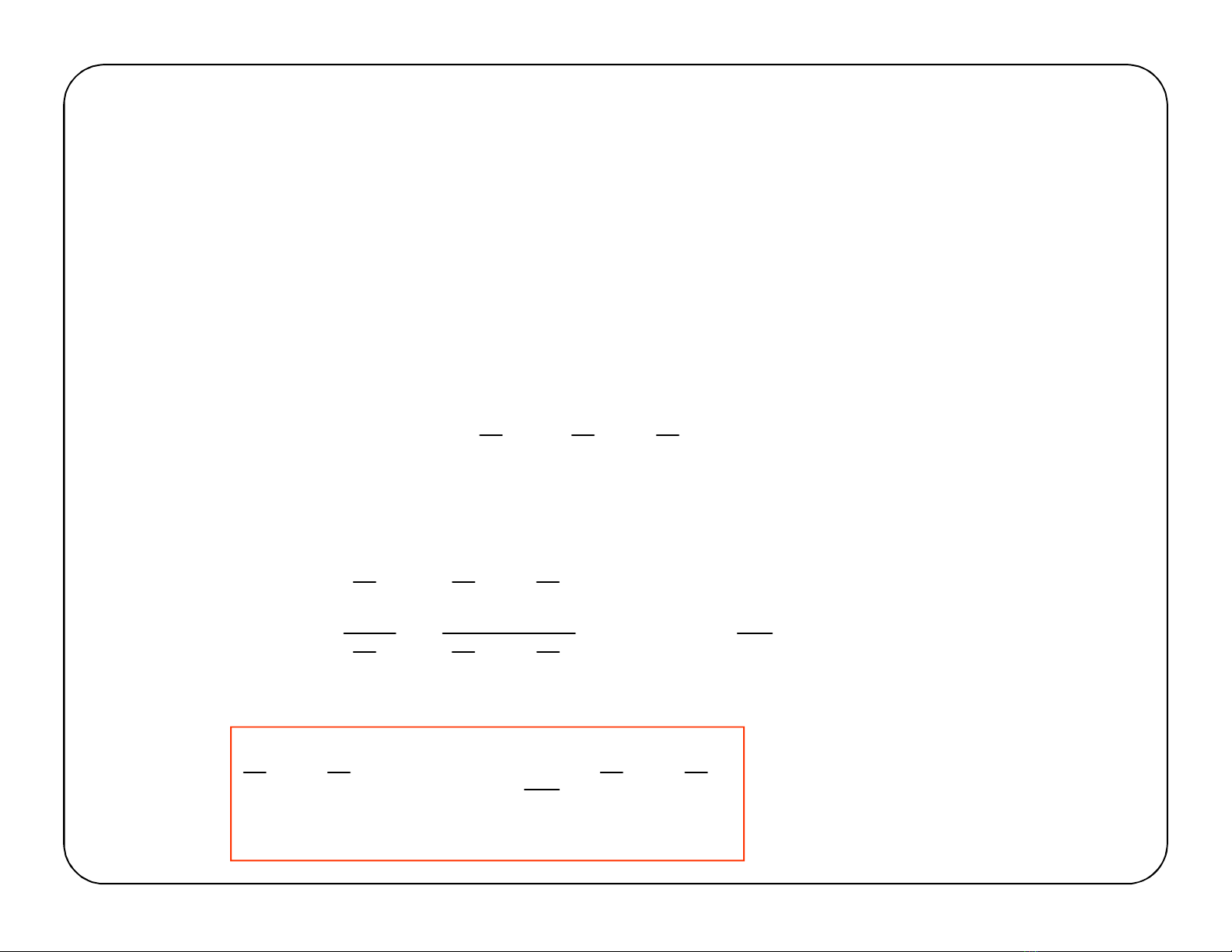
Đê có thê sư dụng được công thức tính động học của hê bánh
răng thường ta cần phải chọn 1 hê qui chiếu mới sao cho đối
với hê qui chiếu mới này tất cả các tâm của các bánh răng
trong hê đều cô định. Ta chọn cần làm hê qui chiếu mới, lúc
này vận tốc góc tương đối của bánh răng thứ k đối với cần sẽ
được tính như sau:
r
k k c
Tỷ sô truyền tương đối của bánh răng thứ j đối với bánh răng
thứ k.
1 .
r
m
j j c
r
k
jk r
k k c j
r
i
1 . .
mk
j c k c
j
r
r
Đây là công
thức Willis cho
bài toán vận
tốc.
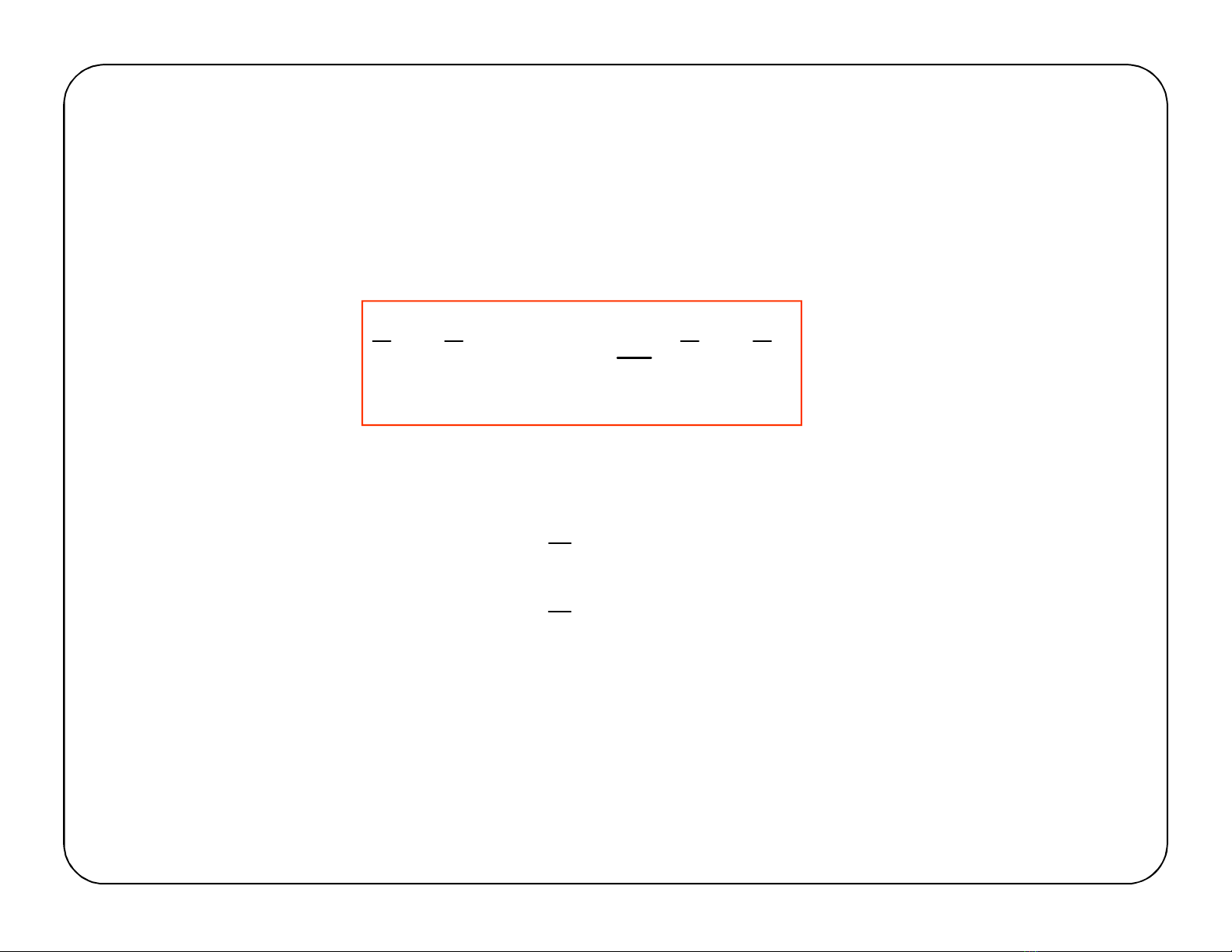
Công thức Willis cho bài toán gia tốc:
Đạo hàm 2 vế của công thức Willis cho bài toán vận tốc theo
thời gian ta sẽ được công thức Willis cho bài toán gia tốc.
ck
j
k
m
cj r
r
..1
Ghi chú:
Chọn:
0
0
c
c